Коэффициент Пуассона

В материаловедении и механике твердого тела коэффициент Пуассона (символ: ν ( nu )) является мерой эффекта Пуассона , деформации (расширения или сжатия) материала в направлениях, перпендикулярных определенному направлению нагрузки . Значение коэффициента Пуассона является отрицательным отношением поперечной деформации к осевой деформации . Для малых значений этих изменений ν представляет собой величину поперечного удлинения, деленную на величину осевого сжатия . Большинство материалов имеют значения коэффициента Пуассона в диапазоне от 0,0 до 0,5. Для мягких материалов, ^[1] таких как резина, где объемный модуль упругости намного выше модуля сдвига, коэффициент Пуассона близок к 0,5. Для полимерных пен с открытыми ячейками коэффициент Пуассона близок к нулю, поскольку ячейки имеют тенденцию разрушаться при сжатии. Многие типичные твердые тела имеют коэффициенты Пуассона в диапазоне от 0,2 до 0,3. Соотношение названо в честь французского математика и физика Симеона Пуассона .

Коэффициент Пуассона является мерой эффекта Пуассона, явления, при котором материал имеет тенденцию расширяться в направлениях, перпендикулярных направлению сжатия. И наоборот, если материал растягивается, а не сжимается, он обычно имеет тенденцию сжиматься в направлениях, поперечных направлению растяжения. Это обычное наблюдение, когда резиновая лента растягивается, она становится заметно тоньше. Опять же, коэффициент Пуассона будет отношением относительного сжатия к относительному расширению и будет иметь то же значение, что и выше. В некоторых редких случаях ^[2] материал фактически будет сжиматься в поперечном направлении при сжатии (или расширяться при растяжении), что даст отрицательное значение коэффициента Пуассона.

Коэффициент Пуассона стабильного, изотропного , линейно- упругого материала должен быть в пределах от −1,0 до +0,5 из-за требования, чтобы модуль Юнга , модуль сдвига и модуль объемной упругости имели положительные значения. ^[3] Большинство материалов имеют значения коэффициента Пуассона в пределах от 0,0 до 0,5. Совершенно несжимаемый изотропный материал, упруго деформируемый при малых деформациях, будет иметь коэффициент Пуассона ровно 0,5. Большинство сталей и жестких полимеров при использовании в пределах их проектных ограничений (до текучести ) демонстрируют значения около 0,3, увеличиваясь до 0,5 для деформации после текучести, которая происходит в основном при постоянном объеме. ^[4] У резины коэффициент Пуассона составляет около 0,5. Коэффициент Пуассона пробки близок к 0, показывая очень небольшое боковое расширение при сжатии, а у стекла он составляет от 0,18 до 0,30. Некоторые материалы, например, некоторые полимерные пены, оригами-складки ^{[5] [6]} и некоторые клетки могут демонстрировать отрицательный коэффициент Пуассона и называются ауксетическими материалами . Если эти ауксетические материалы растягиваются в одном направлении, они становятся толще в перпендикулярном направлении. Напротив, некоторые анизотропные материалы, такие как углеродные нанотрубки , зигзагообразные складчатые листовые материалы ^{[7] [8]} и сотовые ауксетические метаматериалы ^[9] и многие другие, могут демонстрировать один или несколько коэффициентов Пуассона выше 0,5 в определенных направлениях.

Предположим, что материал растягивается или сжимается только в одном направлении ( ось x на диаграмме ниже):

${\displaystyle \nu =- {\frac {d\varepsilon _ {\mathrm {trans} }}{d\varepsilon _ {\mathrm {axis} }}} = - {\frac {d\varepsilon _ {\mathrm {y} }}{d\varepsilon _ {\mathrm {x} }}} = - {\frac {d\varepsilon _ {\ mathrm {z} }}{d\varepsilon _ {\ mathrm {x} }}}}$

где

• ν — результирующий коэффициент Пуассона,
• ε _trans — поперечная деформация
• ε _axial — осевая деформация

и положительная деформация указывает на растяжение, а отрицательная деформация указывает на сжатие.

Для куба, растянутого в направлении x (см. рисунок 1) с увеличением длины на Δ L в направлении x и уменьшением длины на Δ L ′ в направлениях y и z , бесконечно малые диагональные деформации определяются как

${\displaystyle d\varepsilon _{x}={\frac {dx}{x}},\qquad d\varepsilon _{y}={\frac {dy}{y}},\qquad d\varepsilon _{z}={\frac {dz}{z}}.}$

Если коэффициент Пуассона постоянен при деформации, то интегрирование этих выражений и использование определения коэффициента Пуассона дает

${\displaystyle -\nu \int _{L}^{L+\Delta L}{\frac {dx}{x}}=\int _{L}^{L+\Delta L'}{\frac {dy}{y}} = \int _{L}^{L+\Delta L'}{\frac {dz}{z}}.}$

Решая и возводя в степень, получаем соотношение между Δ L и Δ L ′ :

${\displaystyle \left(1+{\frac {\Delta L}{L}}\right)^{-\nu }=1+{\frac {\Delta L'}{L}}.}$

Для очень малых значений Δ L и Δ L ′ приближение первого порядка дает:

${\displaystyle \nu \approx - {\frac {\Delta L'}{\Delta L}}.}$

Относительное изменение объема ⁠ΔV​/В⁠ куба из-за растяжения материала теперь можно вычислить. Поскольку V = L ³ и

${\displaystyle V+\Delta V=(L+\Delta L)\left(L+\Delta L'\right)^{2}}$

можно вывести

${\displaystyle {\frac {\Delta V}{V}}=\left(1+{\frac {\Delta L}{L}}\right)\left(1+{\frac {\Delta L'}{L}}\right)^{2}-1}$

Используя полученное выше соотношение между Δ L и Δ L ′ :

${\displaystyle {\frac {\Delta V}{V}} =\left(1+{\frac {\Delta L}{L}}\right)^{1-2\nu }-1}$

и для очень малых значений Δ L и Δ L ′ приближение первого порядка дает:

${\displaystyle {\frac {\Delta V}{V}}\approx (1-2\nu) {\frac {\Delta L}{L}}}$

Для изотропных материалов можно использовать соотношение Ламе ^[10]

${\displaystyle \nu \approx {\frac {1}{2}}-{\frac {E}{6K}}}$

где K — модуль объемной упругости , а E — модуль Юнга .

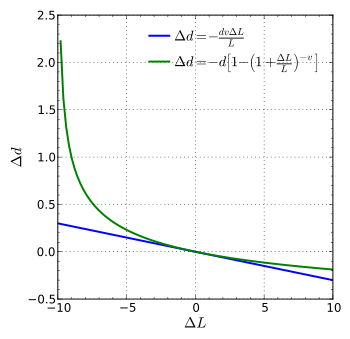
Если стержень диаметром (шириной или толщиной) d и длиной L подвергается растяжению так, что его длина изменится на Δ L , то его диаметр d изменится на:

${\displaystyle {\frac {\Delta d}{d}}=-\nu {\frac {\Delta L}{L}}}$

Приведенная выше формула верна только в случае малых деформаций; если деформации велики, то можно использовать следующую (более точную) формулу:

${\displaystyle \Delta d=-d\left(1-{\left(1+{\frac {\Delta L}{L}}\right)}^{-\nu }\right)}$

где

• d — исходный диаметр
• Δ d — изменение диаметра стержня
• ν — коэффициент Пуассона
• L — исходная длина до растяжения
• Δ L — изменение длины.

Значение отрицательное, поскольку оно уменьшается с увеличением длины.

Для линейного изотропного материала, подверженного только сжимающим (т.е. нормальным) силам, деформация материала в направлении одной оси вызовет деформацию материала вдоль другой оси в трех измерениях. Таким образом, можно обобщить закон Гука (для сжимающих сил) на три измерения:

${\displaystyle {\begin{align}\varepsilon _{xx}&={\frac {1}{E}}\left[\sigma _{xx}-\nu \left(\sigma _{yy}+\sigma _{zz}\right)\right]\\[6px]\varepsilon _{yy}&={\frac {1}{E}}\left[\sigma _{yy}-\nu \left(\sigma _{zz}+\sigma _{xx}\right)\right]\\[6px]\varepsilon _{zz}&={\frac {1}{E}}\left[\sigma _{zz}-\nu \left(\sigma _{xx}+\sigma _{yy}\right)\right]\end{align}}}$^{[ необходима ссылка ]}

где:

• ε _xx , ε _yy и ε _zz — деформации в направлении x , y и z
• σ _xx , σ _yy и σ _zz — напряжения в направлении x , y и z
• E — модуль Юнга (одинаков во всех направлениях для изотропных материалов)
• ν — коэффициент Пуассона (одинаков во всех направлениях для изотропных материалов)

Все эти уравнения можно синтезировать следующим образом:

${\displaystyle \varepsilon _{ii}={\frac {1}{E}}\left[\sigma _{ii}(1+\nu)-\nu \sum _{k}\sigma _{kk}\right]}$

В самом общем случае касательные напряжения будут иметь место наряду с нормальными напряжениями, и полное обобщение закона Гука имеет вид:

${\displaystyle \varepsilon _{ij}={\frac {1}{E}}\left[\sigma _{ij}(1+\nu)-\nu \delta _{ij}\sum _{k}\sigma _{kk}\right]}$

где δ _ij — дельта Кронекера . Обычно принимается обозначение Эйнштейна :

${\displaystyle \sigma _{kk}\equiv \sum _{l}\delta _{kl}\sigma _{kl}}$

записать уравнение просто как:

${\displaystyle \varepsilon _{ij} = {\frac {1}{E}} \left[\sigma _{ij}(1+\nu)-\nu \delta _{ij}\sigma _{kk}\right]}$

Для анизотропных материалов коэффициент Пуассона зависит от направления растяжения и поперечной деформации.

${\displaystyle {\begin{aligned}\nu (\mathbf {n},\mathbf {m})&=-E\left(\mathbf {n} \right)s_{ij\alpha \beta }n_{i}n_{j}m_{\alpha }m_{\beta }\\[4px]E^{-1}(\mathbf {n} )&=s_{ij\alpha \beta }n_{i}n_{j}n_{\alpha }n_{\beta }\end{aligned}}}$

Здесь ν — коэффициент Пуассона, E — модуль Юнга , n — единичный вектор, направленный вдоль направления растяжения, m — единичный вектор, направленный перпендикулярно направлению растяжения. Коэффициент Пуассона имеет разное количество специальных направлений в зависимости от типа анизотропии. ^{[11] [12]}

Ортотропные материалы имеют три взаимно перпендикулярные плоскости симметрии в своих материальных свойствах. Примером может служить древесина, которая наиболее жесткая (и прочная) вдоль волокон и менее жесткая в других направлениях.

Тогда закон Гука можно выразить в матричной форме как ^{[13] [14]}

${\displaystyle {\begin{bmatrix}\epsilon _{xx}\\\epsilon _{yy}\\\epsilon _{zz}\\2\epsilon _{yz}\\2\epsilon _{zx}\\2\epsilon _{xy}\end{bmatrix}}={\begin{bmatrix}{\tfrac {1}{E_{x}}}&-{\tfrac {\nu _{yx}}{E_{y}}}&-{\tfrac {\nu _{zx}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xy}}{E_{x}}}&{\tfrac {1}{E_{y}}}&-{\tfrac {\nu _{zy}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xz}}{E_{x}}}&-{\tfrac {\nu _{yz}}{E_{y}}}&{\tfrac {1}{E_{z}}}&0&0&0\\0&0&0&{\tfrac {1}{G_{yz}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{zx}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{xy}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{yz}\\\sigma _{zx}\\\sigma _{xy}\end{bmatrix}}}$

где

• E _i — модуль Юнга вдоль оси i
• G _ij — модуль сдвига в направлении j на плоскости, нормаль которой направлена ​​в направлении i.
• ν _ij — коэффициент Пуассона, соответствующий сжатию в направлении j при приложении расширения в направлении i .

Коэффициент Пуассона ортотропного материала различен в каждом направлении ( x , y и z ). Однако симметрия тензоров напряжения и деформации подразумевает, что не все шесть коэффициентов Пуассона в уравнении являются независимыми. Существует только девять независимых свойств материала: три модуля упругости, три модуля сдвига и три коэффициента Пуассона. Оставшиеся три коэффициента Пуассона можно получить из соотношений

${\displaystyle {\frac {\nu _{yx}}{E_{y}}}={\frac {\nu _{xy}}{E_{x}}}\,,\qquad {\frac {\nu _{zx}}{E_{z}}}={\frac {\nu _{xz}}{E_{x}}}\,,\qquad {\frac {\nu _{yz}}{E_{y}}}={\frac {\nu _{zy}}{E_{z}}}}$

Из приведенных выше соотношений видно, что если E _x > E _y , то ν _xy > ν _yx . Большее отношение (в данном случае ν _xy ) называется большим коэффициентом Пуассона , а меньшее (в данном случае ν _yx ) называется малым коэффициентом Пуассона . Аналогичные соотношения можно найти и между другими коэффициентами Пуассона.

Трансверсально изотропные материалы имеют плоскость изотропии, в которой упругие свойства изотропны. Если предположить, что эта плоскость изотропии есть yz -плоскость, то закон Гука примет вид ^[15]

${\displaystyle {\begin{bmatrix}\epsilon _{xx}\\\epsilon _{yy}\\\epsilon _{zz}\\2\epsilon _{yz}\\2\epsilon _{zx}\\2\epsilon _{xy}\end{bmatrix}}={\begin{bmatrix}{\tfrac {1}{E_{x}}}&-{\tfrac {\nu _{yx}}{E_{y}}}&-{\tfrac {\nu _{zx}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xy}}{E_{x}}}&{\tfrac {1}{E_{y}}}&-{\tfrac {\nu _{zy}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xz}}{E_{x}}}&-{\tfrac {\nu _{yz}}{E_{y}}}&{\tfrac {1}{E_{z}}}&0&0&0\\0&0&0&{\tfrac {1}{G_{\rm {yz}}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{\rm {zx}}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{\rm {xy}}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{yz}\\\sigma _{zx}\\\sigma _{xy}\end{bmatrix}}}$

где мы использовали yz -плоскость изотропии для уменьшения числа констант, то есть,

${\displaystyle E_{y}=E_{z},\qquad \nu _{xy}=\nu _{xz},\qquad \nu _{yx}=\nu _{zx}.}$.

Симметрия тензоров напряжений и деформаций подразумевает, что

${\displaystyle {\frac {\nu _{xy}}{E_{x}}}={\frac {\nu _{yx}}{E_{y}}},\qquad \nu _{yz}=\nu _{zy}.}$

Это оставляет нам шесть независимых констант E _x , E _y , G _xy , G _yz , ν _xy , ν _yz . Однако поперечная изотропия приводит к дополнительному ограничению между G _yz и E _y , ν _{yz ,} которое равно

${\displaystyle G_{yz}={\frac {E_{y}}{2\left(1+\nu _{yz}\right)}}.}$

Таким образом, существует пять независимых упругих свойств материала, два из которых являются коэффициентами Пуассона. Для предполагаемой плоскости симметрии большее из ν _xy и ν _yx является основным коэффициентом Пуассона. Остальные основные и второстепенные коэффициенты Пуассона равны.

Материал	Коэффициент Пуассона
резина	0,4999 [17]
золото	0,42–0,44
насыщенная глина	0,40–0,49
магний	0,252–0,289
титан	0,265–0,34
медь	0,33
алюминиевый сплав	0,32
глина	0,30–0,45
нержавеющая сталь	0,30–0,31
сталь	0,27–0,30
чугун	0,21–0,26
песок	0,20–0,455
конкретный	0,1–0,2
стекло	0,18–0,3
металлические очки	0,276–0,409 [18]
мыло	0,10–0,50
пробка	0.0

Материал	Плоскость симметрии	ν ху	ν ух	νyz​	ν zy	ν zx	ν xz
Сотовый сердечник Nomex	xy , лента в направлении x	0,49	0,69	0.01	2.75	3.88	0.01
стекловолокно эпоксидная смола	ху	0,29	0,32	0,06	0,06	0,32

Некоторые материалы, известные как ауксетичные материалы, демонстрируют отрицательный коэффициент Пуассона. При воздействии положительной деформации по продольной оси поперечная деформация в материале фактически будет положительной (т. е. она увеличит площадь поперечного сечения). Для этих материалов это обычно происходит из-за уникально ориентированных шарнирных молекулярных связей. Для того чтобы эти связи растягивались в продольном направлении, шарниры должны «открыться» в поперечном направлении, эффективно демонстрируя положительную деформацию. ^[19] Это также можно сделать структурированным способом и привести к новым аспектам в проектировании материалов, как для механических метаматериалов .

Исследования показали, что некоторые виды твердой древесины демонстрируют отрицательный коэффициент Пуассона исключительно во время испытания на ползучесть при сжатии . ^{[20] [21]} Первоначально испытание на ползучесть при сжатии показывает положительный коэффициент Пуассона, но постепенно уменьшается, пока не достигнет отрицательных значений. Следовательно, это также показывает, что коэффициент Пуассона для древесины зависит от времени при постоянной нагрузке, что означает, что деформация в осевом и поперечном направлении не увеличивается с одинаковой скоростью.

Среды с искусственной микроструктурой могут демонстрировать отрицательный коэффициент Пуассона. В простом случае ауксетичность достигается путем удаления материала и создания периодической пористой среды. ^[22] Решетки могут достигать более низких значений коэффициента Пуассона, ^[23] которые могут быть бесконечно близки к предельному значению −1 в изотропном случае. ^[24]

Более трехсот кристаллических материалов имеют отрицательный коэффициент Пуассона. ^{[25] [26] [27]} Например, Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS ₂ и другие.

При конечных деформациях соотношение между поперечной и осевой деформациями ε _trans и ε _axial обычно не очень хорошо описывается коэффициентом Пуассона. Фактически, коэффициент Пуассона часто считается функцией приложенной деформации в режиме большой деформации. В таких случаях коэффициент Пуассона заменяется функцией Пуассона, для которой существует несколько конкурирующих определений. ^[28] Определяя поперечное растяжение λ _trans = ε _trans + 1 и осевое растяжение λ _axial = ε _axial + 1 , где поперечное растяжение является функцией осевого растяжения, наиболее распространенными являются функции Генки, Био, Грина и Альманси:

${\displaystyle {\begin{aligned}\nu ^{\text{Hencky}}&=-{\frac {\ln \lambda _{\text{trans}}}{\ln \lambda _{\text{axial}}}}\\[6pt]\nu ^{\text{Biot}}&={\frac {1-\lambda _{\text{trans}}}{\lambda _{\text{axial}}-1}}\\[6pt]\nu ^{\text{Green}}&={\frac {1-\lambda _{\text{trans}}^{2}}{\lambda _{\text{axial}}^{2}-1}}\\[6pt]\nu ^{\text{Almansi}}&={\frac {\lambda _{\text{trans}}^{-2}-1}{1-\lambda _{\text{axial}}^{-2}}}\end{aligned}}}$

Одной из областей, в которой эффект Пуассона оказывает значительное влияние, является поток в трубе под давлением. Когда воздух или жидкость внутри трубы находятся под высоким давлением, они оказывают равномерное усилие на внутреннюю часть трубы, что приводит к кольцевому напряжению внутри материала трубы. Из-за эффекта Пуассона это кольцевое напряжение приведет к увеличению диаметра трубы и небольшому уменьшению ее длины. Уменьшение длины, в частности, может оказать заметное влияние на стыки труб, поскольку эффект будет накапливаться для каждой секции трубы, соединенной последовательно. Защемленное соединение может быть разорвано или иным образом подвержено разрушению. ^{[ необходима цитата ]}

Другая область применения эффекта Пуассона — структурная геология . Горные породы, как и большинство материалов, подвержены эффекту Пуассона, находясь под напряжением. В геологическом масштабе времени чрезмерная эрозия или седиментация земной коры может либо создавать, либо устранять большие вертикальные напряжения на подстилающей породе. Эта порода будет расширяться или сжиматься в вертикальном направлении как прямой результат приложенного напряжения, а также будет деформироваться в горизонтальном направлении в результате эффекта Пуассона. Это изменение деформации в горизонтальном направлении может влиять на соединения и спящие напряжения в породе или образовывать их. ^[29]

Хотя пробка исторически выбиралась для закупорки винных бутылок по другим причинам (включая ее инертность, непроницаемость, гибкость, герметичность и упругость), ^[30] коэффициент Пуассона пробки, равный нулю, обеспечивает еще одно преимущество. Когда пробка вставляется в бутылку, верхняя часть, которая еще не вставлена, не расширяется в диаметре, поскольку она сжимается в осевом направлении. Сила, необходимая для вставки пробки в бутылку, возникает только из-за трения между пробкой и бутылкой из-за радиального сжатия пробки. Если бы пробка была сделана из резины, например, (с коэффициентом Пуассона около +0,5), потребовалась бы относительно большая дополнительная сила для преодоления радиального расширения верхней части резиновой пробки.

Большинство автомехаников знают, что резиновый шланг (например, шланг охлаждающей жидкости) трудно снять с металлического патрубка, так как натяжение при натяжении приводит к сжатию диаметра шланга, который плотно сжимает патрубок. (Этот же эффект показан в китайской ловушке для пальцев .) Шланги легче снять с патрубков, используя широкое плоское лезвие.

• Линейная эластичность
• закон Гука
• Методика импульсного возбуждения
• Ортотропный материал
• Модуль сдвига
• модуль Юнга
• Коэффициент теплового расширения

• Значение коэффициента Пуассона
• Материалы с отрицательным коэффициентом Пуассона
• Подробнее о материалах с отрицательным коэффициентом Пуассона (ауксетических) Архивировано 08.02.2018 на Wayback Machine

Формулы преобразования
Упругие свойства однородных изотропных линейно-упругих материалов однозначно определяются любыми двумя модулями из них; таким образом, если заданы любые два модуля упругости, любой другой модуль упругости может быть рассчитан по этим формулам, как для трехмерных материалов (первая часть таблицы), так и для двумерных материалов (вторая часть).
3D формулы	${\displaystyle K=\,}$	${\displaystyle E=\,}$	${\displaystyle \lambda =\,}$	${\displaystyle G=\,}$	${\displaystyle \nu =\,}$	${\displaystyle M=\,}$	Примечания
${\displaystyle (K,\,E)}$			${\displaystyle {\tfrac {3K(3K-E)}{9K-E}}}$	${\displaystyle {\tfrac {3KE}{9K-E}}}$	${\displaystyle {\tfrac {3K-E}{6K}}}$	${\displaystyle {\tfrac {3K(3K+E)}{9K-E}}}$
${\displaystyle (K,\,\lambda )}$		${\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}}$		${\displaystyle {\tfrac {3(K-\lambda )}{2}}}$	${\displaystyle {\tfrac {\lambda }{3K-\lambda }}}$	${\displaystyle 3K-2\lambda \,}$
${\displaystyle (K,\,G)}$		${\displaystyle {\tfrac {9KG}{3K+G}}}$	${\displaystyle K-{\tfrac {2G}{3}}}$		${\displaystyle {\tfrac {3K-2G}{2(3K+G)}}}$	${\displaystyle K+{\tfrac {4G}{3}}}$
${\displaystyle (K,\,\nu )}$		${\displaystyle 3K(1-2\nu )\,}$	${\displaystyle {\tfrac {3K\nu }{1+\nu }}}$	${\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}}$		${\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}}$
${\displaystyle (K,\,M)}$		${\displaystyle {\tfrac {9K(M-K)}{3K+M}}}$	${\displaystyle {\tfrac {3K-M}{2}}}$	${\displaystyle {\tfrac {3(M-K)}{4}}}$	${\displaystyle {\tfrac {3K-M}{3K+M}}}$
${\displaystyle (E,\,\lambda )}$	${\displaystyle {\tfrac {E+3\lambda +R}{6}}}$			${\displaystyle {\tfrac {E-3\lambda +R}{4}}}$	${\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}}$	${\displaystyle {\tfrac {E-\lambda +R}{2}}}$	${\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}}$
${\displaystyle (E,\,G)}$	${\displaystyle {\tfrac {EG}{3(3G-E)}}}$		${\displaystyle {\tfrac {G(E-2G)}{3G-E}}}$		${\displaystyle {\tfrac {E}{2G}}-1}$	${\displaystyle {\tfrac {G(4G-E)}{3G-E}}}$
${\displaystyle (E,\,\nu )}$	${\displaystyle {\tfrac {E}{3(1-2\nu )}}}$		${\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}}$	${\displaystyle {\tfrac {E}{2(1+\nu )}}}$		${\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}}$
${\displaystyle (E,\,M)}$	${\displaystyle {\tfrac {3M-E+S}{6}}}$		${\displaystyle {\tfrac {M-E+S}{4}}}$	${\displaystyle {\tfrac {3M+E-S}{8}}}$	${\displaystyle {\tfrac {E-M+S}{4M}}}$		${\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}}$ Есть два допустимых решения. Знак плюс приводит к .${\displaystyle \nu \geq 0}$ Знак минус приводит к .${\displaystyle \nu \leq 0}$
${\displaystyle (\lambda ,\,G)}$	${\displaystyle \lambda +{\tfrac {2G}{3}}}$	${\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}}$			${\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}}$	${\displaystyle \lambda +2G\,}$
${\displaystyle (\lambda ,\,\nu )}$	${\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}}$	${\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}}$		${\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}}$		${\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}}$	Не может быть использовано, когда${\displaystyle \nu =0\Leftrightarrow \lambda =0}$
${\displaystyle (\lambda ,\,M)}$	${\displaystyle {\tfrac {M+2\lambda }{3}}}$	${\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}}$		${\displaystyle {\tfrac {M-\lambda }{2}}}$	${\displaystyle {\tfrac {\lambda }{M+\lambda }}}$
${\displaystyle (G,\,\nu )}$	${\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}}$	${\displaystyle 2G(1+\nu )\,}$	${\displaystyle {\tfrac {2G\nu }{1-2\nu }}}$			${\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}}$
${\displaystyle (G,\,M)}$	${\displaystyle M-{\tfrac {4G}{3}}}$	${\displaystyle {\tfrac {G(3M-4G)}{M-G}}}$	${\displaystyle M-2G\,}$		${\displaystyle {\tfrac {M-2G}{2M-2G}}}$
${\displaystyle (\nu ,\,M)}$	${\displaystyle {\tfrac {M(1+\nu )}{3(1-\nu )}}}$	${\displaystyle {\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}}$	${\displaystyle {\tfrac {M\nu }{1-\nu }}}$	${\displaystyle {\tfrac {M(1-2\nu )}{2(1-\nu )}}}$
2D формулы	${\displaystyle K_{\mathrm {2D} }=\,}$	${\displaystyle E_{\mathrm {2D} }=\,}$	${\displaystyle \lambda _{\mathrm {2D} }=\,}$	${\displaystyle G_{\mathrm {2D} }=\,}$	${\displaystyle \nu _{\mathrm {2D} }=\,}$	${\displaystyle M_{\mathrm {2D} }=\,}$	Примечания
${\displaystyle (K_{\mathrm {2D} },\,E_{\mathrm {2D} })}$			${\displaystyle {\tfrac {2K_{\mathrm {2D} }(2K_{\mathrm {2D} }-E_{\mathrm {2D} })}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }E_{\mathrm {2D} }}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }-E_{\mathrm {2D} }}{2K_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {4K_{\mathrm {2D} }^{2}}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle (K_{\mathrm {2D} },\,\lambda _{\mathrm {2D} })}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }(K_{\mathrm {2D} }-\lambda _{\mathrm {2D} })}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$		${\displaystyle K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$	${\displaystyle 2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}$
${\displaystyle (K_{\mathrm {2D} },\,G_{\mathrm {2D} })}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D} }-G_{\mathrm {2D} }}$		${\displaystyle {\tfrac {K_{\mathrm {2D} }-G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D} }+G_{\mathrm {2D} }}$
${\displaystyle (K_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$		${\displaystyle 2K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{1+\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2K_{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$
${\displaystyle (E_{\mathrm {2D} },\,G_{\mathrm {2D} })}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }G_{\mathrm {2D} }}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2G_{\mathrm {2D} }(E_{\mathrm {2D} }-2G_{\mathrm {2D} })}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2G_{\mathrm {2D} }}}-1}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }^{2}}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle (E_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1-\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }\nu _{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1+\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$
${\displaystyle (\lambda _{\mathrm {2D} },\,G_{\mathrm {2D} })}$	${\displaystyle \lambda _{\mathrm {2D} }+G_{\mathrm {2D} }}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(\lambda _{\mathrm {2D} }+G_{\mathrm {2D} })}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$	${\displaystyle \lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }\,}$
${\displaystyle (\lambda _{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}{\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{\nu _{\mathrm {2D} }}}}$	Не может быть использовано, когда${\displaystyle \nu _{\mathrm {2D} }=0\Leftrightarrow \lambda _{\mathrm {2D} }=0}$
${\displaystyle (G_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{1-\nu _{\mathrm {2D} }}}}$	${\displaystyle 2G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2G_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {2G_{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$
${\displaystyle (G_{\mathrm {2D} },\,M_{\mathrm {2D} })}$	${\displaystyle M_{\mathrm {2D} }-G_{\mathrm {2D} }}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(M_{\mathrm {2D} }-G_{\mathrm {2D} })}{M_{\mathrm {2D} }}}}$	${\displaystyle M_{\mathrm {2D} }-2G_{\mathrm {2D} }\,}$		${\displaystyle {\tfrac {M_{\mathrm {2D} }-2G_{\mathrm {2D} }}{M_{\mathrm {2D} }}}}$