Пасьянс «Пег»

Peg Solitaire , Solo Noble , Solo Goli , Marble Solitaire или просто Solitaire — настольная игра для одного игрока, в которой нужно передвигать колышки по доске с отверстиями. В некоторых наборах используются шарики на доске с углублениями. В Великобритании игра известна как Solitaire, а в США, где «Solitaire» теперь является общепринятым названием для слова « pasten », — как Peg Solitaire .
Первые свидетельства об игре можно проследить до двора Людовика XIV , и конкретная дата 1697 год, с гравюрой, сделанной десять лет спустя Клодом Огюстом Береем, изображающей Анну де Роган-Шабо , принцессу Субиз, с головоломкой рядом с ней. Выпуск французского литературного журнала Mercure galant за август 1697 года содержит описание доски, правил и примеров задач. Это первое известное упоминание об игре в печати.
Стандартная игра заполняет всю доску колышками, за исключением центрального отверстия. Цель состоит в том, чтобы, делая допустимые ходы, очистить всю доску, за исключением единственного колышка в центральном отверстии.
Доска
Существуют две традиционные доски («.» как начальный колышек, «o» как начальное отверстие):
| Английский | европейский |
|---|---|
· · · · · · · · · · · · · · · · о · · · · · · · · · · · · · · · · | · · · · · · · · · · · · · · · · · · о · · · · · · · · · · · · · · · · · · |
Играть


Допустимым ходом является перепрыгивание колышка через соседний колышек в отверстие, расположенное на две позиции дальше, а затем удаление перепрыгнутого колышка.
На следующих схемах ·обозначает колышек в отверстии, *жирный обозначает колышек, который нужно переместить, а oобозначает пустое отверстие. Синий ¤— это отверстие, из которого переместился текущий колышек; красный *— это конечное положение этого колышка, красный o— это отверстие колышка, который был перепрыгнут и удален.
Таким образом, допустимыми ходами в каждом из четырех ортогональных направлений являются:
* · o → ¤ o * Перейти вправо
o · * → * o ¤ Перейти влево
* ¤ · → o Прыжок вниз o *
o * · → o Перейти вверх * ¤
На английской доске первые три хода могут быть такими:
· · · · · · · · · · · · · · * · · ¤ · · о · · * ·· · · · · · · · · · · о · · · · ¤ о * · · · · оо о · · ·· · · o · · · · · · · * · · · · · · · · · · · · ¤ · · ·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Стратегия
Существует множество различных решений стандартной задачи, и одна из нотаций, используемых для их описания, присваивает отверстиям буквы (хотя могут использоваться и цифры):
английский европейский abcabc defydefzghijklmghijklmнетpx PON нетpx PONМЛКЖИХГМЛКЖИХГ ФЕДЗФЕДЫ CBACBA
Эта зеркальная нотация используется, помимо прочего, потому, что на европейской доске один набор альтернативных игр начинается с отверстия в некоторой позиции и заканчивается одним колышком в его зеркальном положении. На английской доске эквивалентные альтернативные игры начинаются с отверстия и заканчиваются колышком в той же позиции.
Не существует решения для европейской доски с начальным отверстием, расположенным в центре, если разрешены только ортогональные ходы. Это легко увидеть следующим образом, по аргументу Ханса Зантемы . Разделим позиции доски на позиции A, B и C следующим образом:
АБВ АБВАБАБКАБКАBCABCABКАБКАБЦ BCABC АБВ
Первоначально, когда свободна только центральная позиция, число покрытых позиций A равно 12, число покрытых позиций B равно 12, а также число покрытых позиций C равно 12. После каждого хода число покрытых позиций A увеличивается или уменьшается на единицу, и то же самое касается числа покрытых позиций B и числа покрытых позиций C. Следовательно, после четного числа ходов все эти три числа четные, а после нечетного числа ходов все эти три числа нечетные. Следовательно, конечная позиция только с одним колышком не может быть достигнута, так как для этого потребовалось бы, чтобы одно из этих чисел было единицей (позиция колышка, единица нечетная), в то время как другие два числа были нулевыми, следовательно, четными.
Однако существует несколько других конфигураций, в которых одно исходное отверстие можно свести к одному колышку.
Тактика, которую можно использовать, состоит в том, чтобы разделить доску на пакеты по три и полностью очистить (удалить) их, используя один дополнительный колышек, катализатор, который выскакивает , а затем снова выскакивает . В примере ниже * — это катализатор.:
* · o ¤ o * o * · * o ¤ · → · → o → o · · ¤ о
Эту технику можно использовать с линией из 3 штифтов, блоком из 2,3 штифтов и 6-штифтовой L-образной фигурой с основанием длиной 3 штифта и стойкой длиной 4 штифта.
Другие альтернативные игры включают начало с двумя пустыми отверстиями и окончание с двумя колышками в этих отверстиях. Также начало с одного отверстия здесь и окончание одним колышком там . На английской доске отверстие может быть где угодно, а последний колышек может оказаться только там, где разрешено кратно трем. Таким образом , отверстие в a может оставить только один колышек в a , p , O или C.
Исследования по игре в пасьянс «колышек»
Известен тщательный анализ игры. [1] Этот анализ ввел понятие, называемое функцией пагоды , которая является мощным инструментом для демонстрации неразрешимости данной обобщенной задачи пасьянса «колышек».
Решение для нахождения функции пагоды, демонстрирующее неразрешимость данной задачи, формулируется как задача линейного программирования и решается за полиномиальное время. [2]
В статье 1990 года рассматривались обобщенные задачи Hi-Q, которые эквивалентны задачам о пасьянсе, и была показана их NP-полнота . [3]
В статье 1996 года была сформулирована задача пасьянса «колышек» как задача комбинаторной оптимизации и обсуждались свойства допустимой области, называемой «конусом пасьянса». [4]
В 1999 году пасьянс «колышек» был полностью решен на компьютере с помощью исчерпывающего перебора всех возможных вариантов. Это было достигнуто с помощью симметрии, эффективного хранения созвездий доски и хеширования. [5]
В 2001 году был разработан эффективный метод решения задач на пасьянс «Пег». [2]
Неопубликованное исследование 1989 года по обобщенной версии игры на английской доске показало, что каждая возможная проблема в обобщенной игре имеет 2 9 возможных различных решений, исключая симметрии, поскольку английская доска содержит 9 различных подквадратов 3×3. Одним из следствий этого анализа является установление нижней границы размера возможных задач «перевернутого положения», в которых изначально занятые клетки остаются пустыми и наоборот. Любое решение такой задачи должно содержать минимум 11 ходов, независимо от точных деталей задачи.
С помощью абстрактной алгебры можно доказать , что существует только 5 фиксированных позиций на доске, где игра может успешно закончиться с одним колышком. [6]
Решения для английской игры
Кратчайшее решение стандартной английской игры включает 18 ходов, считая множественные прыжки одним ходом:
| Самое короткое решение английского пасьянса «колышек» |
|---|
бывший lj ck · · · · · · · · · · · ¤ · * · · ¤ · · o · · o o · · · · · · · · · · o · · · · · · * o ¤ · · · · · * о ·· · · o · · · · · · · * · · · · · · · · · · · · · · · ·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · Пф ДП ГИ ДжХ · · о · · о · · о · · о · о * · о · · о · · о ·· · · · о о · · · · · оо · · · · · оо · · · · · оо ·· · · · ¤ · · · · · · * · · · · · · · · · · · · · · · ·· · · · · · · · · · · o · · · · · · * o ¤ · · · ¤ o * o · · · · · ¤ · · о · · о · · · · · · · · · · · · · mGI ik gi LJHljh · · о · · о · · о · · о · о · · о · · о · · о ·· · · · оо ¤ · · ¤ о * оо ¤ о * о · ооо * о о о о о· · · · · · о · · · · · · о · · · · · · о · · · · · о о· · · о * о о · · · о · оо · · · о · оо · ¤ о о о о о · · о · · о · · о · · о · · · · · · · · · · · · · CK pF ACK Mgi · · о · · о · · о · · о · о · · о · · о · · о ·о · ооооо · ооооо · ооооо о * оооо · · · · · оо · · ¤ · · оо · · о · · оо о · о · · оо· о * оооо · о о ооо · о * оооо ¤ о · оооо о · о * · о о · оо · о ¤ · · о · · о о ¤ ооо ackI dpFDPp ox ¤ о о ооооо · о о ¤ оооооо · о о ооо о ооооооооо · о · о ооо · * о о ооо ¤ о * ооооо · о * оооо о о о оооооооо о · о о о о оо оооооооо Порядок некоторых ходов можно поменять местами. Обратите внимание, что если вместо этого вы думаете о * как о дырке, а о как о колышек, вы можете решить головоломку, следуя решению в обратном порядке, начиная с последней картинки, идя к первому. Однако для этого требуется более 18 ходов. |
Это решение было найдено в 1912 году Эрнестом Бергхолтом и доказано Джоном Бизли в 1964 году как самое короткое из возможных. [7]
Это решение можно также увидеть на странице, где также представлена нотация Вольстенхолма, призванная облегчить запоминание решения.
Другие решения включают следующий список. В них используется обозначение
- Список стартовых лунок
- Колон
- Список конечных целевых колышков
- Знак равенства
- Исходный колышек и отверстие назначения (перепрыгнутые колышки оставлены в качестве упражнения для читателя)
- , или / ( косая черта используется для разделения «кусков», например, six-purge out )
x:x=ex,lj,ck,Pf,DP,GI,JH,mG,GI,ik,gi,LJ,JH,Hl,lj,jh,CK,pF,AC,CK,Mg,gi,ac, ck,kI,dp,pF,FD,DP,Pp,ox x:x=ex,lj,xe/hj,Ki,jh/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK, LJ/PD,GI,mG,JH,GI,DP/Ox j:j=lj,Ik,jl/hj,Ki,jh/mk,Gm,Hl,fP,mk,Pf/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/Jj i:i=ki,Jj,ik/lj,Ik,jl/AI,FD,CA,HJ,AI,JH/mk,Hl,Gm,fP,mk,Pf/ai,ca,fd,hj,ai, jh/gi,Mg,Lh,pd,gi,dp/Ki e:e=xe/lj,Ik,jl/ck,ac,df,lj,ck,jl/GI,lH,mG,DP,GI,PD/AI,FD,CA,JH,AI,HJ/pF, MK,gM,JL,MK,Fp/hj,ox,xe d:d=fd,xe,df/lj,ck,ac,Pf,ck,jl/DP,KI,PD/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/МК,gM,hL,пФ,МК,Фп/пд б:b=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp, ox/xe/AI/BJ,JH,Hl,lj,jb б:x=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp, ox/xe/AI/BJ,JH,HL,lj,ex a:a=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/dp,gi,pd,Mg,Lh,gi/ia a:p=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/dp,gi,pd,Mg,Lh,gi/dp

Атака методом грубой силы на стандартный английский пасьянс «колышек»
Единственное место, где можно оказаться с единственным колышком, — это центр или середина одного из краев; при последнем прыжке всегда будет возможность выбрать, остановиться ли в центре или на краю.
Ниже приведена таблица с количеством ( P ossible Board P ositions ) возможных позиций на доске после n прыжков и вероятностью того же колышка, перемещенного для совершения еще одного прыжка ( N o F urther J umps). Интересно отметить, что кратчайший путь к провалу игры — за шесть ходов, а решение (помимо его вращений и отражений) уникально. Вот пример этого: 4 → 16; 23 → 9; 14 → 16; 17 → 15; 19 → 17; 31 → 23. (В этой нотации колышки нумеруются слева направо, начиная с 0 и двигаясь вниз по каждой строке и в крайнее левое положение после того, как каждая строка отмечена.)
ПРИМЕЧАНИЕ: Если одну позицию на доске можно повернуть и/или перевернуть в другую позицию на доске, позиции на доске считаются идентичными.
|
|
|
|
Поскольку возможно только 31 прыжок, современные компьютеры могут легко проверить все игровые позиции за разумное время. [8]
Вышеуказанная последовательность "PBP" была введена как A112737 в OEIS . Обратите внимание, что общее количество достижимых позиций на доске (сумма последовательности) составляет 23 475 688, в то время как общее количество возможных позиций на доске составляет 8 589 934 590 (33 бита-1) (2^33), поэтому только около 2,2% всех возможных позиций на доске могут быть достигнуты, начиная с пустого центра.
Также возможно сгенерировать все позиции доски. Результаты ниже были получены с использованием набора инструментов mCRL2 (см. пример peg_solitaire в дистрибутиве).
|
|
|
|
В представленных ниже результатах он сгенерировал все позиции на доске, которых он действительно достиг, начиная с пустого центра и заканчивая центральной лункой.
|
|
|
|
Решения для европейской игры
Существует 3 исходных неконгруэнтных положения, которые имеют решения. [9] Это:
1)
0 1 2 3 4 5 6 0 о · · 1 · · · · · 2 · · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·
Возможное решение: [2:2-0:2, 2:0-2:2, 1:4-1:2, 3:4-1:4, 3:2-3:4, 2:3-2:1, 5:3-3:3, 3:0-3:2, 5:1-3:1, 4:5-4:3, 5:5-5:3, 0:4-2:4, 2:1-4:1, 2:4-4:4, 5:2-5:4, 3:6-3:4, 1:1-1:3, 2:6-2:4, 0:3-2:3, 3:2-5:2, 3:4-3:2, 6:2-4:2, 3:2-5:2, 4:0-4:2, 4:3-4:1, 6:4-6:2, 6:2-4:2, 4:1-4:3, 4:3-4:5, 4:6-4:4, 5:4-3:4, 3:4-1:4, 1:5-1:3, 2:3-0:3, 0:2-0:4]
2)
0 1 2 3 4 5 6 0 · · · 1 · · о · · 2 · · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·
Возможное решение: [1:1-1:3, 3:2-1:2, 3:4-3:2, 1:4-3:4, 5:3-3:3, 4:1-4:3, 2:1-4:1, 2:6-2:4, 4:4-4:2, 3:4-1:4, 3:2-3:4, 5:1-3:1, 4:6-2:6, 3:0-3:2, 4:5-2:5, 0:2-2:2, 2:6-2:4, 6:4-4:4, 3:4-5:4, 2:3-2:1, 2:0-2:2, 1:4-3:4, 5:5-5:3, 6:3-4:3, 4:3-4:1, 6:2-4:2, 3:2-5:2, 4:0-4:2, 5:2-3:2, 3:2-1:2, 1:2-1:4, 0:4-2:4, 3:4-1:4, 1:5-1:3, 0:3-2:3]
и 3)
0 1 2 3 4 5 6 0 · · · 1 · · · · · 2 · · · о · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·
Возможное решение: [2:1-2:3, 0:2-2:2, 4:1-2:1, 4:3-4:1, 2:3-4:3, 1:4-1:2, 2:1-2:3, 0:4-0:2, 4:4-4:2, 3:4-1:4, 6:3-4:3, 1:1-1:3, 4:6-4:4, 5:1-3:1, 2:6-2:4, 1:4-1:2, 0:2-2:2, 3:6-3:4, 4:3-4:1, 6:2-4:2, 2:3-2:1, 4:1-4:3, 5:5-5:3, 2:0-2:2, 2:2-4:2, 3:4-5:4, 4:3-4:1, 3:0-3:2, 6:4-4:4, 4:0-4:2, 3:2-5:2, 5:2-5:4, 5:4-3:4, 3:4-1:4, 1:5-1:3]
Варианты плат
В пасьянс «колышек» играли и на досках других размеров, хотя две из них, приведенные выше, являются наиболее популярными. В него также играли на треугольной доске, с прыжками во всех трех направлениях. Если вариант имеет надлежащую «четность» и достаточно большой, он, вероятно, будет разрешим.
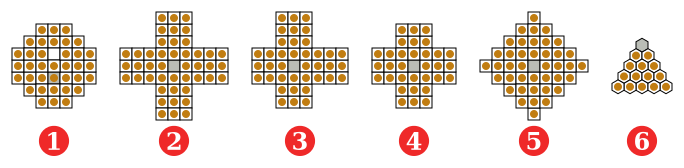
(1) французский (европейский) стиль, 37 лунок, 17 век;
(2) JC Wiegleb, 1779, Германия, 45 лунок;
(3) асимметричный 3-3-2-2, описанный Джорджем Беллом, 20 век; [10]
(4) английский стиль (стандартный), 33 лунки;
(5) ромб, 41 лунка;
(6) треугольник, 15 лунок.
Серый = лунка для выжившего.
Обычный треугольный вариант имеет пять колышков на стороне. Решение, при котором последний колышек прибывает в начальное пустое отверстие, невозможно для отверстия в одной из трех центральных позиций. Установка пустого угла-отверстия может быть решена за десять ходов, а установка пустого середины-отверстия за девять (Bell 2008):
| Кратчайшее решение треугольного варианта |
|---|
* = колышек для следующего хода; ¤ = отверстие, созданное ходом; o = колышек, через который был сделан прыжок, удален; * = отверстие, заполненное прыжком; · · · * ¤ · · · · · · · * o ¤ · · · · · · * · · ¤ · · * o · · · · · · · · · · · · · · o · · * * · * * · о · · ¤ о * * · о * о ¤ · о · * о · о · · о · оооо * * * * ¤ ¤ оооо о о о о * * о о о оо * оо ¤ ¤ · · ¤ о о о ооо * * оо · о оо о оо * * о · о ¤ ¤ о · оооо * ооо ¤ оо * оо |
Видеоигра
26 июня 1992 года видеоигра на основе пасьянса «колышек» была выпущена для Game Boy. Названная просто Solitaire , игра была разработана Hect. В Северной Америке DTMC выпустила игру под названием Lazlos' Leap .
В популярной культуре
Игра Shivers для ПК , игра-головоломка в жанре ужасов point and click , предлагает множество головоломок/игр, которые игрок должен решить. Головоломка под названием «Chinese Checkers» на самом деле является пасьянсом с колышками.
Cracker Barrel представляет игру на каждом столе в своих филиалах. Доска, представленная в игре, треугольная с 15 общими отверстиями.
В фильме «Ковбой Бибоп: Фильм» главный антагонист Винсент Воладжу проводит большую часть своего свободного времени, играя в пасьянс. Вектор для его запланированной атаки Биотерроризма , тип нанобота , хранится в шариках пасьянса.
Ссылки
- ^ Берлекамп, Э. Р .; Конвей, Дж. Х .; Гай, Р. К. (2001) [1981], Выигрышные пути для ваших математических игр (2-е изд.), AK Peters/CRC Press, ISBN 978-1568811307, OCLC 316054929
- ^ ab Kiyomi, M.; Matsui, T. (2001), "Алгоритмы на основе целочисленного программирования для задач пасьянса", Proc. 2nd Int. Conf. Computers and Games (CG 2000): Алгоритмы на основе целочисленного программирования для задач пасьянса , Lecture Notes in Computer Science, vol. 2063, pp. 229–240, CiteSeerX 10.1.1.65.6244 , doi :10.1007/3-540-45579-5_15, ISBN 978-3-540-43080-3
- ^ Уэхара, Р.; Ивата, С. (1990). «Обобщенный Hi-Q является NP-полным». Trans. IEICE . 73 : 270–273.
- ^ Авис, Д.; Деза, А. (2001), «О конусе солитера и его связи с многопродуктовыми потоками», Математическое программирование , 90 (1): 27–57, doi :10.1007/PL00011419, S2CID 7852133
- ^ Эйхлер; Йегер; Людвиг (1999), октябрь 07/1999 Spielverderber, Solitaire mit dem Computer lösen (на немецком языке), vol. 7, с. 218
- ^ "Mathematics and brainvita", Notes on Mathematics , 28 августа 2012 г. , получено 6 сентября 2018 г.
- ↑ Доказательство Бизли см. в книге «Winning Ways» , том № 4 (второе издание).
- ^ "solboard". github . 2020-08-31 . Получено 2020-08-31 .
Реализация расчета методом перебора в игре Peg Solitaire
- ^ Брассин, Мишель (декабрь 1981), "Découvrez... le solitaire", Jeux et Strategie (на французском языке)
- ^ См. Обобщенные крестовые доски в: Страница пасьянса «Пег» Джорджа
Дальнейшее чтение
- Бисли, Джон Д. (1985), «Пасьянс с головоломкой «Пег» изнутри» , Oxford University Press , ISBN 978-0198532033
- Белл, GI (2008), «Решение треугольного пасьянса», Журнал целочисленных последовательностей , 11 : Статья 08.4.8, arXiv : math.CO/0703865 , Bibcode : 2007math......3865B.
- Bruijn, NG de (1972), «Игра в пасьянс и ее связь с конечным полем» (PDF) , Journal of Recreational Mathematics , 5 : 133–137, архивировано (PDF) из оригинала 2022-10-09
- Кросс, Д.К. (1968), «Квадратный пасьянс и его вариации», Журнал занимательной математики , 1 : 121–123
- Гарднер, М. , «Математические игры», Scientific American 206 (6): 156–166, июнь 1962 г.; 214 (2): 112–113, февраль 1966 г.; 214 (5): 127, май 1966 г.
- Джефферсон, Крис и др. (октябрь 2006 г.), «Моделирование и решение английского пасьянса Peg Solitairet», Computers & Operations Research , 33 (10): 2935–2959, CiteSeerX 10.1.1.5.7805 , doi :10.1016/j.cor.2005.01.018
Внешние ссылки
- Богомольный, Александр, «Пасьянс «Колышек» и теория групп», Interactive Mathematics Miscellany and Puzzles , получено 7 сентября 2018 г.
- Белые пиксели (24 октября 2017 г.), Peg Solitaire: Легко запоминающееся симметричное решение (видео), Youtube, заархивировано с оригинала 2021-12-11
