Прямое квадратурно-нулевое преобразование
Прямая квадратурно-нулевая ( DQZ или DQ0 [1] или DQO , [2] иногда строчные буквы) трансформация или нулевая прямая квадратурная [3] ( 0DQ или ODQ , иногда строчные буквы) трансформация — это тензор , который вращает систему отсчета трехэлементного вектора или матрицы размером три на три элемента в попытке упростить анализ. Преобразование DQZ является произведением преобразования Кларка и преобразования Парка, впервые предложенного в 1929 году Робертом Х. Парком . [4]
Преобразование DQZ часто используется в контексте электротехники с трехфазными цепями . Преобразование может использоваться для вращения опорных систем сигналов переменного тока таким образом, чтобы они стали сигналами постоянного тока . Затем можно выполнить упрощенные вычисления для этих величин постоянного тока перед выполнением обратного преобразования для восстановления фактических результатов трехфазного переменного тока. Например, преобразование DQZ часто используется для упрощения анализа трехфазных синхронных машин или для упрощения вычислений для управления трехфазными инверторами . При анализе трехфазных синхронных машин преобразование переводит трехфазные величины статора и ротора в одну вращающуюся опорную систему для устранения эффекта изменяющихся во времени индуктивностей и преобразования системы в линейную систему, не зависящую от времени.
Введение
Преобразование DQZ состоит из матриц преобразования Парка и Кларка. Преобразование Кларка (названное в честь Эдит Кларк ) преобразует векторы в системе отсчета ABC в систему отсчета XYZ (также называемую αβγ ). Основное значение преобразования Кларка заключается в изоляции той части вектора, ссылающегося на ABC , которая является общей для всех трех компонентов вектора; оно изолирует синфазный компонент (т. е. компонент Z ). Инвариантная по мощности, правосторонняя, равномерно масштабированная матрица преобразования Кларка имеет вид
- .
Чтобы преобразовать вектор-столбец, ссылающийся на ABC , в систему отсчета XYZ , вектор необходимо предварительно умножить на матрицу преобразования Кларка:
- .
И для обратного преобразования из столбцового вектора, ссылающегося на XYZ , в систему отсчета ABC вектор необходимо предварительно умножить на матрицу обратного преобразования Кларка:
- .
Преобразование Парка (названное в честь Роберта Х. Парка ) преобразует векторы в системе отсчета XYZ в систему отсчета DQZ . Основное значение преобразования Парка — поворот системы отсчета вектора на произвольной частоте. Преобразование Парка сдвигает спектр частот сигнала таким образом, что произвольная частота теперь отображается как «dc», а старый dc отображается как отрицательная часть произвольной частоты. Матрица преобразования Парка имеет вид
- ,
где θ — мгновенный угол произвольной частоты ω . Для преобразования вектора, отнесенного к XYZ , в систему отсчета DQZ сигнал вектора-столбца должен быть предварительно умножен на матрицу преобразования Парка:
- .
А для обратного преобразования из вектора, связанного с DQZ , в систему отсчета XYZ сигнал вектора-столбца должен быть предварительно умножен на матрицу обратного преобразования Парка:
- .
Преобразования Кларка и Парка вместе образуют преобразование DQZ :
Обратное преобразование:
Чтобы преобразовать вектор, ссылающийся на ABC , в систему отсчета DQZ , сигнал вектора столбца должен быть предварительно умножен на матрицу преобразования DQZ:
- .
И для обратного преобразования из вектора, ссылающегося на DQZ , в систему отсчета ABC , сигнал вектора-столбца должен быть предварительно умножен на матрицу обратного преобразования DQZ:
- .
Для лучшего понимания этого преобразования включен его вывод.
Вывод
Вывод преобразования Парка
Преобразование Парка основано на концепции скалярного произведения и проекций векторов на другие векторы. Сначала представим два единичных вектора и (единичные векторы или оси новой системы отсчета с точки зрения старой системы отсчета) и третий, произвольный, вектор . Мы можем определить два единичных вектора и случайный вектор в терминах их декартовых координат в старой системе отсчета:
- ,
где и — единичные базисные векторы старой системы координат, а — угол между единичными векторами и (т.е. угол между двумя системами отсчета). Проекция произвольного вектора на каждый из двух новых единичных векторов подразумевает скалярное произведение:
- .
Итак, — это проекция на ось, а — это проекция на ось. Эти новые векторные компоненты и вместе составляют новый вектор , исходный вектор в терминах новой системы отсчета DQ .

Обратите внимание, что положительный угол выше заставил произвольный вектор повернуться назад при переходе в новую систему отсчета DQ . Другими словами, его угол относительно новой системы отсчета меньше, чем его угол относительно старой системы отсчета. Это происходит потому, что система отсчета, а не вектор, была повернута вперед. На самом деле, прямое вращение системы отсчета идентично отрицательному вращению вектора. Если старая система отсчета вращалась вперед, например, в трехфазных электрических системах, то результирующий вектор DQ остается неподвижным.
Одно матричное уравнение может суммировать вышеприведенную операцию:
- .
Этот тензор можно расширить до трехмерных задач, где ось, вокруг которой происходит вращение, остается нетронутой. В следующем примере вращение происходит вокруг оси Z , но можно было выбрать любую ось:
- .
С точки зрения линейной алгебры это просто вращение по часовой стрелке вокруг оси z и математически эквивалентно тригонометрическим формулам разностного угла .
Вывод преобразования Кларка
Базисные векторы единичной системы ABC
Рассмотрим трехмерное пространство с единичными базисными векторами A , B и C. Сфера на рисунке ниже используется для отображения масштаба системы отсчета для контекста, а прямоугольник используется для предоставления вращательного контекста.

Обычно в электротехнике (или любом другом контексте, где используются трехфазные системы) трехфазные компоненты показаны в двухмерной перспективе. Однако, учитывая, что три фазы могут изменяться независимо, они по определению ортогональны друг другу. Это подразумевает трехмерную перспективу, как показано на рисунке выше. Таким образом, двухмерная перспектива на самом деле показывает проекцию трехмерной реальности на плоскость.
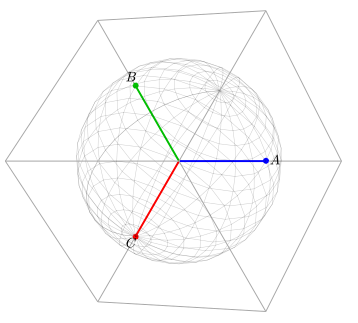
Трехфазные проблемы обычно описываются как работающие в этой плоскости. В действительности проблема, скорее всего, является проблемой сбалансированной фазы (т.е. v A + v B + v C = 0) и чистый вектор
всегда находится в этом плане.
Базисные векторы единичного AYC
Для построения преобразования Кларка мы фактически используем преобразование Парка в два шага. Наша цель — повернуть ось C в угол коробки. Таким образом, повернутая ось C будет ортогональна плоскости двумерной перспективы, упомянутой выше. Первый шаг к построению преобразования Кларка требует вращения системы отсчета ABC вокруг оси A. Итак, на этот раз 1 будет в первом элементе преобразования Парка:
На следующем рисунке показано, как система отсчета ABC поворачивается в систему отсчета AYC' , когда любой вектор предварительно умножается на матрицу K 1. Оси C' и Y теперь указывают на середины краев ящика, но величина системы отсчета не изменилась (т. е. сфера не увеличилась и не уменьшилась). Это связано с тем, что норма тензора K 1 равна 1: || K 1 || = 1. Это означает, что любой вектор в системе отсчета ABC будет продолжать иметь ту же величину при повороте в систему отсчета AYC' .
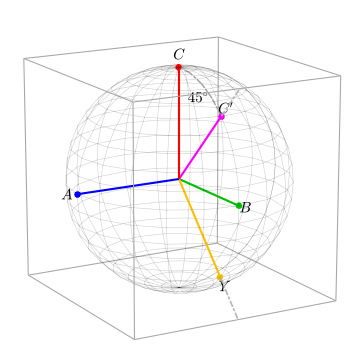
Базисные векторы XYZ
Далее следующий тензор вращает вектор вокруг новой оси Y против часовой стрелки относительно оси Y (угол был выбран таким образом, чтобы ось C' была направлена к углу коробки.):
- ,
или
- .
Обратите внимание, что расстояние от центра сферы до середины края коробки равно √ 2 , а от центра сферы до угла коробки равно √ 3. Вот откуда взялся угол 35,26°. Угол можно вычислить с помощью скалярного произведения. Пусть будет единичным вектором в направлении C' , а будет единичным вектором в направлении угла коробки в . Поскольку где угол между и мы имеем
Норма матрицы K 2 также равна 1, поэтому она также не изменяет величину любого вектора, предварительно умноженного на матрицу K 2 .
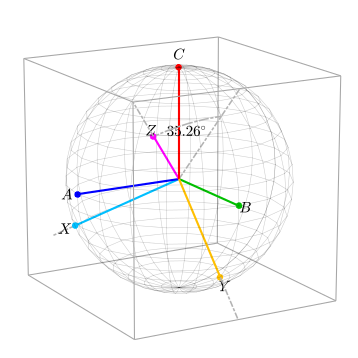
Нулевая плоскость
В этой точке ось Z теперь ортогональна плоскости, в которой может быть найден любой вектор ABC без синфазной составляющей. Любая сбалансированная векторная форма волны ABC (вектор без синфазной составляющей) будет перемещаться вокруг этой плоскости. Эта плоскость будет называться нулевой плоскостью и показана ниже шестиугольным контуром.
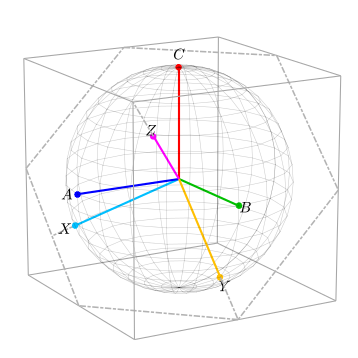
Базисные векторы X и Y находятся на нулевой плоскости. Обратите внимание, что ось X параллельна проекции оси A на нулевую плоскость. Ось X немного больше проекции оси A на нулевую плоскость. Она больше в √ 3/2 раза . Произвольный вектор не изменил величину при этом преобразовании из системы отсчета ABC в систему отсчета XYZ (т. е. сфера не изменила размер). Это справедливо для степенно-инвариантной формы преобразования Кларка. На следующем рисунке показана общая двумерная перспектива систем отсчета ABC и XYZ .

Может показаться странным, что хотя величина вектора не изменилась, изменилась величина его компонентов (т. е. компоненты X и Y длиннее, чем компоненты A , B и C ). Возможно, это можно интуитивно понять, если учесть, что для вектора без синфазного сигнала то, что требовало для выражения трех значений ( компоненты A , B и C ), теперь требует только 2 ( компоненты X и Y ), поскольку компонент Z равен нулю. Следовательно, значения компонентов X и Y должны быть больше для компенсации.
Комбинация тензоров
Матрица преобразования Кларка, инвариантная по степени, представляет собой комбинацию тензоров K 1 и K 2 :
- ,
или
- .
Обратите внимание, что при умножении нижняя строка матрицы K C равна 1/ √ 3 , а не 1/3. (Эдит Кларк использовала 1/3 для случая степенного варианта.) Компонент Z не является точным средним значением компонентов A , B , и C . Если бы только элементы нижней строки были изменены на 1/3, то сфера была бы сжата вдоль оси Z. Это означает, что компонент Z не имел бы того же масштаба, что и компоненты X и Y.
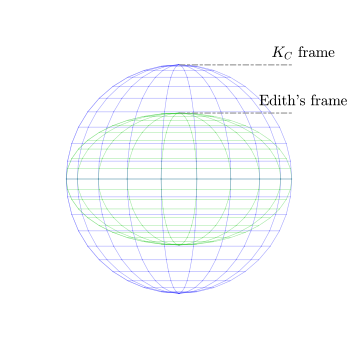
Как написано выше, норма матрицы преобразования Кларка по-прежнему равна 1, что означает, что она только вращает вектор ABC , но не масштабирует его. Того же самого нельзя сказать об исходном преобразовании Кларка.
Легко проверить (путем умножения матриц), что обратная матрица для K C равна
Форма варианта мощности
Иногда желательно масштабировать матрицу преобразования Кларка так, чтобы ось X была проекцией оси A на нулевую плоскость. Чтобы сделать это, мы равномерно применяем масштабный коэффициент √ 2/3 и радикал 2 √ 1/ [ почему? ] к нулевому компоненту, чтобы получить степенную матрицу преобразования Кларка:
или
- .
Это обязательно уменьшит сферу в √ 2/3 раза , как показано ниже. Обратите внимание, что эта новая ось X является в точности проекцией оси A на нулевую плоскость.

При степенном варианте преобразования Кларка величина произвольного вектора меньше в системе отсчета XYZ , чем в системе отсчета ABC (норма преобразования равна √ 2/3 ), но величины отдельных векторных компонентов одинаковы (когда нет синфазного сигнала). Так, например, сигнал, определяемый как
становится, в системе отсчета XYZ ,
- ,
новый вектор, компоненты которого имеют ту же величину, что и исходные компоненты: 1. Во многих случаях это выгодное качество степенного варианта преобразования Кларка.
Преобразование DQZ
Преобразование DQZ использует преобразование Кларка для преобразования векторов, относящихся к ABC, в два компонента дифференциального режима (т. е. X и Y ) и один компонент синфазного режима (т. е. Z ), а затем применяет преобразование Парка для вращения системы отсчета вокруг оси Z на некоторый заданный угол. Компонент X становится компонентом D , который находится в прямом выравнивании с вектором вращения, а компонент Y становится компонентом Q , который находится под углом квадратуры к прямому компоненту. Преобразование DQZ является
- .
Пример
В электрических системах очень часто значения A , B и C колеблются таким образом, что вектор-результат вращается. В сбалансированной системе вектор вращается вокруг оси Z. Очень часто бывает полезно вращать систему отсчета таким образом, чтобы большинство изменений значений abc, вызванных этим вращением, были аннулированы, а любые более мелкие изменения стали более очевидными. Это невероятно полезно, поскольку теперь преобразует систему в линейную систему, инвариантную во времени
Преобразование DQZ можно рассматривать в геометрических терминах как проекцию трех отдельных синусоидальных фазовых величин на две оси, вращающиеся с той же угловой скоростью, что и синусоидальные фазовые величины.

Выше показано преобразование DQZ, примененное к статору синхронной машины. Имеется три обмотки, разделенные 120 физическими градусами. Три фазных тока равны по величине и разделены друг от друга на 120 электрических градусов. Три фазных тока отстают от соответствующих фазных напряжений на . Оси DQ показаны вращающимися с угловой скоростью, равной , той же угловой скорости, что и фазные напряжения и токи. Ось D составляет угол с фазной обмоткой A , которая была выбрана в качестве опорной. Токи и являются постоянными величинами постоянного тока.
Сравнение с другими преобразованиями
Трансформация Парка
Первоначально предложенное Парком в [5] преобразование несколько отличается от приведенного выше. В преобразовании Парка ось q находится впереди оси d, qd0, а угол — это угол между фазой a и осью d, как показано ниже:
и
Д. Холмс и Т. Липо, Широтно-импульсная модуляция для преобразователей мощности: принципы и практика, Wiley-IEEE Press, 2003, и
П. Краузе, О. Васинчук и С. Судхофф, Анализ электрических машин и систем привода, 2-е изд., Пискатауэй, Нью-Джерси: IEEE Press, 2002.
αβγ преобразование
Преобразование dqo концептуально похоже на преобразование αβγ . В то время как преобразование dqo является проекцией фазовых величин на вращающуюся двухосную систему отсчета, преобразование αβγ можно рассматривать как проекцию фазовых величин на неподвижную двухосную систему отсчета.
Ссылки
- Встроенные ссылки
- ^ "Выполнить преобразование из трехфазного (abc) сигнала во вращающуюся систему отсчета dq0 или обратно". Simulink . 2018-09-27 . Получено 2019-01-11 .
- ^ Михайлович, Зоран (1998-06-26). "Моделирование и проектирование систем привода Vsi-Fed Pmsm с активной нагрузкой" (PDF) . ETD . Получено 2019-01-11 .
- ^ Камалаканнан, C.; Суреш, LP; Дэш, SS; Паниграхи, BK (2014). Силовая электроника и возобновляемые энергетические системы: Труды ICPERES 2014. Конспект лекций по электротехнике. Springer India. стр. 1029. ISBN 978-81-322-2119-7. Получено 11.01.2019 .
- ^ RH Park. Теория двухреакционных синхронных машин. Труды AIEE 48:716–730 (1929).
- ^ RH Park, «Двухреакционная теория синхронных машин, обобщенный метод анализа — часть I», в Трудах Американского института инженеров-электриков, т. 48, № 3, стр. 716-727, июль 1929 г., doi: 10.1109/T-AIEE.1929.5055275
- Общие ссылки
- CJ O'Rourke и др. «Геометрическая интерпретация систем отсчета и преобразований: dq0, Кларк и Парк», в IEEE Transactions on Energy Conversion, т. 34, № 4, стр. 2070-2083, декабрь 2019 г.
- Дж. Льюис Блэкберн Симметричные компоненты для проектирования энергосистем , Марсель Деккер, Нью-Йорк (1993). ISBN 0-8247-8767-6
- Чжан и др. Трехфазный инвертор с нейтралью и пространственной векторной модуляцией. Труды конференции IEEE APEC '97 (1997).
- TALipo, «Подход декартовых векторов к референтной теории машин переменного тока», Международная конференция по электрическим машинам, Лозанна, 18–24 сентября 1984 г.




























































