Метод постоянной времени разомкнутой цепи

Метод постоянной времени разомкнутой цепи (OCT) — это метод приближенного анализа, используемый в проектировании электронных схем для определения угловой частоты сложных схем . Это особый случай метода постоянной времени нулевого значения (ZVT), когда реактивные элементы состоят только из конденсаторов. Сам метод постоянной времени нулевого значения (ZVT) является особым случаем общего анализа постоянной времени и передачи (TTC) , который позволяет полностью оценить нули и полюса любых сосредоточенных систем LTI с индукторами и конденсаторами в качестве реактивных элементов, используя постоянные времени и постоянные передачи . Метод OCT обеспечивает быструю оценку и определяет наибольшие вклады в постоянные времени в качестве руководства по улучшению схемы.

Основой метода является приближение, что угловая частота усилителя определяется членом в знаменателе его передаточной функции , который является линейным по частоте. Это приближение может быть крайне неточным в некоторых случаях, когда ноль в числителе близок по частоте. ^[1] Если все полюса действительны и нулей нет, это приближение всегда консервативно, в том смысле, что инверсия суммы постоянных времени нулевого значения меньше фактической угловой частоты схемы. ^[2]

Метод также использует упрощенный метод нахождения линейного по частоте члена, основанного на суммировании RC-произведений для каждого конденсатора в цепи, где резистор R для выбранного конденсатора представляет собой сопротивление, найденное путем вставки тестового источника на его месте и установки всех остальных конденсаторов на ноль. Отсюда и название — метод постоянной времени с нулевым значением .

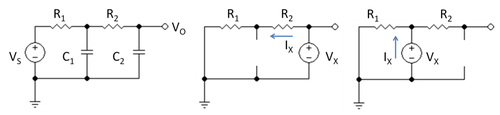
На рисунке 1 показан простой RC фильтр нижних частот. Его передаточная функция находится с использованием закона Кирхгофа следующим образом. На выходе

${\displaystyle {\frac {V_{1}-V_{O}}{R_{2}}}=j\omega C_{2}V_{O}\ ,}$

где V ₁ — напряжение на вершине конденсатора C ₁ . В центральном узле:

${\displaystyle {\frac {V_{S}-V_{1}}{R_{1}}}=j\omega C_{1}V_{1}+{\frac {V_{1}-V_{O} }{R_{2}}}\ .}$

Объединяя эти соотношения, получаем передаточную функцию:

${\displaystyle {\frac {V_{O}}{V_{S}}}={\frac {1}{1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}}}}$

Линейный член по j ω в этой передаточной функции можно вывести следующим методом, который представляет собой применение метода постоянной времени разомкнутой цепи к данному примеру.

1. Установите источник сигнала на ноль.
2. Выберите конденсатор C ₂ , замените его тестовым напряжением V _X , а C ₁ замените разомкнутой цепью. Затем сопротивление, видимое тестовым напряжением, находится с помощью схемы на средней панели рисунка 1 и просто равно V _X / I _X = R ₁ + R ₂ . Образуйте произведение C ₂ ( R ₁ + R ₂ ).
3. Выберите конденсатор C ₁ , замените его тестовым напряжением V _X , а C ₂ замените разомкнутой цепью. Затем сопротивление, видимое тестовым напряжением, находится с помощью схемы на правой панели рисунка 1 и просто равно V _X / I _X = R ₁ . Образуйте произведение C ₁ R ₁ .
4. Добавьте эти термины.

По сути, это похоже на то, как если бы каждый конденсатор заряжался и разряжался через сопротивление, обнаруженное в цепи, в то время как другой конденсатор представляет собой разомкнутую цепь.

Процедура постоянной времени разомкнутой цепи обеспечивает линейный член в j ω независимо от того, насколько сложной становится RC-цепь. Первоначально это было разработано и доказано путем вычисления сопутствующих факторов матрицы проводимости Торнтоном и Сирлом. ^[3] Более интуитивное индуктивное доказательство этого (и других свойств TTC) было позже разработано Хаджимири. ^[4]

Для сложной схемы процедура состоит из следования вышеуказанным правилам, проходя через все конденсаторы в схеме. Более общий вывод можно найти у Грея и Мейера. ^[5]

До сих пор результат был общим, но для его использования вводится приближение: делается предположение, что этот линейный член в j ω определяет угловую частоту схемы.

Это предположение можно рассмотреть более подробно на примере рисунка 1: предположим, что постоянные времени этой цепи равны τ ₁ и τ ₂ ; то есть:

${\displaystyle \left(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2}\right)=1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}}$

Сравнивая коэффициенты линейного и квадратичного членов относительно j ω, получаем:

${\displaystyle \tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\ ,}$

${\displaystyle \tau _{1}\tau _{2}=C_{1}C_{2}R_{1}R_{2}\ .}$

Одна из двух постоянных времени будет самой длинной; пусть это будет τ ₁ . Предположим на мгновение, что она намного больше другой, τ ₁ >> τ ₂ . В этом случае приближения справедливы:

${\displaystyle \tau _{1}+\tau _{2}\approx \tau _{1}\ ,}$

и

${\displaystyle \tau _{2}={\frac {\tau _{1}\tau _{2}}{\tau _{1}}}\approx {\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}\ .}$

Другими словами, подставляя значения RC:

${\displaystyle \tau _{1}\approx {\hat {\tau _{1}}}=\ \tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\ ,}$

и

${\displaystyle \tau _{2}\approx {\hat {\tau _{2}}}={\frac {\tau _{1}\tau _{2}}{\tau _{1}+\ тау _{2}}}={\frac {C_{1}C_{2}R_{1}R_{2}}{C_{2}(R_{1}+R_{2})+C_{1} Р_{1}}}\ ,}$

где ( ^ ) обозначает приблизительный результат. Кстати, обратите внимание, что постоянные времени цепи включают оба конденсатора; другими словами, в общем случае постоянные времени цепи не определяются каким-либо одним конденсатором. Используя эти результаты, легко исследовать, насколько хорошо угловая частота (частота 3 дБ) задается выражением

${\displaystyle f_{3dB}={\frac {1}{2\pi {\hat {\tau _{1}}}}}\ ,}$

так как параметры изменяются. Также точную передаточную функцию можно сравнить с приближенной, то есть,

${\displaystyle {\frac {1}{(1+j\omega \tau _{1})(1+j\omega \tau _{2})}}\ }$ ${\стиль_отображения \ }$   с   ${\стиль_отображения \ }$ ${\displaystyle \ {\frac {1}{(1+j\omega {\hat {\tau _{1}}})(1+j\omega {\hat {\tau _{2}}})} }\ .}$

Конечно, согласие хорошее, если предположение τ ₁ >> τ ₂ верно.

Рисунок 2 иллюстрирует приближение. Ось x — это отношение τ ₁ / τ ₂ в логарифмическом масштабе. Увеличение этой переменной означает, что более высокий полюс находится еще выше угловой частоты. Ось y — это отношение оценки постоянной времени разомкнутой цепи (OCTC) к истинной постоянной времени. Для самого низкого полюса используйте кривую T_1; эта кривая относится к угловой частоте; а для более высокого полюса используйте кривую T_2. Наихудшее согласие достигается при τ ₁ = τ ₂ . В этом случае τ ^{^} ₁ = 2 τ ₁ , а угловая частота в 2 раза меньше. Более высокий полюс в 2 раза больше (его постоянная времени составляет половину реального значения).

Во всех случаях предполагаемая частота угла ближе, чем в два раза от реальной, и всегда консервативна , то есть ниже реального угла, поэтому фактическая схема будет вести себя лучше, чем предсказано. Однако более высокий полюс всегда оптимистичен , то есть предсказывает высокий полюс на более высокой частоте, чем есть на самом деле. Чтобы использовать эти оценки для прогнозирования переходного процесса , которые зависят от соотношения двух полюсных частот (см. статью о расщеплении полюсов для примера), Рисунок 2 показывает, что для точности необходимо довольно большое соотношение τ ₁ / τ ₂ , поскольку ошибки в τ ^{^} ₁ и τ ^{^} ₂ усиливают друг друга в соотношении τ ^{^} ₁ / τ ^{^} ₂ .

Метод постоянной времени разомкнутой цепи фокусируется только на угловой частоте, но, как было показано выше, возможны также оценки для более высоких полюсов.

Применение метода постоянной времени разомкнутой цепи к ряду каскадов усилителя на одном транзисторе можно найти в работах Питтета и Кандасвами. ^[6]