Восьмигранная пирамида
| Восьмигранная пирамида | ||
|---|---|---|
 Диаграмма Шлегеля | ||
| Тип | Многогранная пирамида | |
| Символ Шлефли | ( ) ∨ {3,4} ( ) ∨ г{3,3} ( ) ∨ с{2,6} ( ) ∨ [{4} + { }] ( ) ∨ [{ } + { } + { }] | |
| Клетки | 9 | 1 {3,4}  8 ( ) ∨ {3}  |
| Лица | 20 {3} | |
| Края | 18 | |
| Вершины | 7 | |
| Двойной | Кубическая пирамида | |
| Группа симметрии | B 3 , [4,3,1], порядок 48 [3,3,1], порядок 24 [2 + ,6,1], порядок 12 [4,2,1], порядок 16 [2,2,1], порядок 8 | |
| Характеристики | выпуклый , регулярные ячейки, слепой многогранник | |
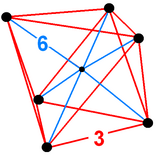
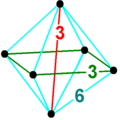
В 4-мерной геометрии октаэдрическая пирамида ограничена одним октаэдром на основании и 8 треугольными пирамидальными ячейками , которые встречаются на вершине. Поскольку октаэдр имеет описанный радиус, деленный на длину ребра меньше единицы, [1] треугольные пирамиды могут быть сделаны с правильными гранями (как правильные тетраэдры ) путем вычисления соответствующей высоты.
Имея все правильные ячейки, это слепой многогранник . Две копии могут быть дополнены, чтобы получить октаэдрическую бипирамиду , которая также является слепым многогранником.
Находки октаэдрической пирамиды
Правильная 16-ячейка имеет октаэдрические пирамиды вокруг каждой вершины, причем октаэдр проходит через центр 16-ячейки. Таким образом, размещение двух правильных октаэдрических пирамид основанием к основанию образует 16-ячейку. 16-ячейка мозаично разбивает 4-мерное пространство как 16-ячеечные соты .
Ровно 24 правильные октаэдрические пирамиды будут располагаться вокруг вершины в четырехмерном пространстве (вершина каждой пирамиды). Эта конструкция дает 24-ячейку с октаэдрическими ограничивающими ячейками, окружающими центральную вершину с 24 большими радиусами длины ребра. 4-мерное содержимое 24-ячейки с единичной длиной ребра равно 2, поэтому содержимое правильной октаэдрической пирамиды равно 1/12. 24-ячейка мозаично разбивает 4-мерное пространство как 24-ячеечные соты .
Восьмигранная пирамида является вершинной фигурой усеченного 5-ортоплекса ,
.
Граф октаэдрической пирамиды является единственным возможным минимальным контрпримером к гипотезе Негами о том, что связные графы с плоскими покрытиями сами по себе являются проективно-планарными. [2]
Пример 4-мерных координат, 6 точек в первых 3 координатах для куба и 4-е измерение для вершины.
- (±1, 0, 0; 0)
- ( 0,±1, 0; 0)
- ( 0, 0, ± 1; 0)
- ( 0, 0, 0; 1)
Другие многогранники
Кубическая пирамида
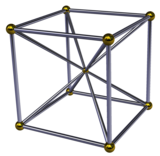
Двойственной октаэдрической пирамиде является кубическая пирамида , рассматриваемая как кубическое основание и 6 квадратных пирамид, встречающихся в вершине .
Пример 4-мерных координат, 8 точек в первых 3 координатах для куба и 4-е измерение для вершины.
- (±1,±1,±1; 0)
- ( 0, 0, 0; 1)
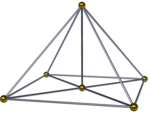
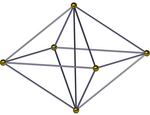
Квадратно-пирамидальная пирамида
| Квадратно-пирамидальная пирамида | ||
|---|---|---|
  | ||
| Тип | Многогранная пирамида | |
| Символ Шлефли | ( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }] | |
| Клетки | 6 | 2 ( )∨{4}  4 ( )∨{3} |
| Лица | 12 {3} 1 {4} | |
| Края | 13 | |
| Вершины | 6 | |
| Двойной | Самодвойственный | |
| Группа симметрии | [4,1,1], порядок 8 [4,2,1], порядок 16 [2,2,1], порядок 8 | |
| Характеристики | выпуклый , с правильной поверхностью | |
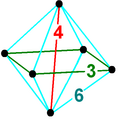
Квадратно -пирамидальная пирамида , ( ) ∨ [( ) ∨ {4}], является разделенной пополам октаэдрической пирамидой. Она имеет квадратное основание пирамиды и 4 тетраэдра вместе с еще одной квадратной пирамидой, встречающейся на вершине. Ее также можно увидеть в проекции с центром на ребре как квадратную бипирамиду с четырьмя тетраэдрами, обернутыми вокруг общего ребра. Если высота двух вершин одинакова, ей можно дать более высокое название симметрии [( ) ∨ ( )] ∨ {4} = { } ∨ {4}, соединяя ребро с перпендикулярным квадратом. [3]
Квадратно -пирамидальная пирамида может быть искажена в прямоугольно-пирамидальную пирамиду , { } ∨ [{ } × { }] или ромбо-пирамидальную пирамиду , { } ∨ [{ } + { }], или другие формы с более низкой симметрией.
Квадратно -пирамидальная пирамида существует как вершинная фигура в однородных многогранниках вида
, включая усеченный 5-ортоплекс и усеченные тессерактовые соты .
Пример 4-мерных координат, 2 координаты для квадрата и осевые точки для пирамидальных точек.
- (±1,±1; 0; 0)
- ( 0, 0; 1; 0)
- ( 0, 0; 0; 1)
Ссылки
- ^ Клитцинг, Ричард. «Трехмерные выпуклые однородные многогранники x3o4o - oct».1/квадратный корень(2) = 0,707107
- ^ Hliněný, Petr (2010), "20 лет гипотезе Negami о плоском покрытии" (PDF) , Графы и комбинаторика , 26 (4): 525–536, CiteSeerX 10.1.1.605.4932 , doi :10.1007/s00373-010-0934-9, MR 2669457, S2CID 121645
- ^ Клитцинг, Ричард. «Сегментотоп скваск, К-4.4».
Внешние ссылки
- Ольшевский, Джордж. "Пирамида". Глоссарий гиперпространства . Архивировано из оригинала 4 февраля 2007 года.
- Клитцинг, Ричард. «4D Сегментотопы».
- Клитцинг, Ричард. «Сегментотоп октапи, К-4.3».
- Ричард Клитцинг, Осесимметричные огранки ребер однородных многогранников
 | Эта статья о 4-многограннике является заглушкой . Вы можете помочь Википедии, расширив ее. |
