Нономино

Геометрическая фигура, образованная из девяти квадратов.

Нономино (или эннеомино или 9-омино ) — это полимино порядка 9; то есть многоугольник на плоскости , состоящий из 9 квадратов одинакового размера , соединенных ребром к ребру. ^[1] Название этого типа фигуры образуется с помощью префикса non(a)-. Если вращения и отражения не считаются различными фигурами, то существует 1285 различных свободных нономино. Если отражения считаются различными, то существует 2500 односторонних нономино. Если вращения также считаются различными, то существует 9910 фиксированных нономино. ^[2]

Симметрия

1285 свободных нономино можно классифицировать в соответствии с их группами симметрии : ^[2]

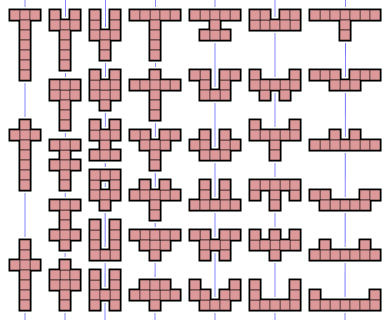
1196 нономино не имеют симметрии . Их группа симметрии состоит только из тождественного отображения .
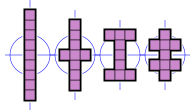
38 нономино имеют ось симметрии отражения, совмещенную с линиями сетки. Их группа симметрии состоит из двух элементов: тождества и отражения относительно линии, параллельной сторонам квадратов.

26 нономино имеют ось симметрии отражения под углом 45° к линиям сетки. Их группа симметрии состоит из двух элементов: тождества и диагонального отражения.

19 нономино обладают точечной симметрией, также известной как вращательная симметрия 2-го порядка. Их группа симметрии состоит из двух элементов: тождества и поворота на 180°.

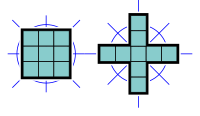
4 нономино имеют две оси симметрии отражения, обе выровненные с линиями сетки. Их группа симметрии состоит из четырех элементов: тождества, двух отражений и поворота на 180°. Это диэдральная группа порядка 2, также известная как четырехгруппа Клейна .

2 нономино имеют четыре оси симметрии отражения, совмещенные с линиями сетки и диагоналями, и вращательную симметрию четвертого порядка. Их группа симметрии, диэдральная группа четвертого порядка, состоит из восьми элементов.

В отличие от октамино , не существует нономино с вращательной симметрией четвертого порядка или с двумя осями симметрии отражения, совмещенными с диагоналями.

Если отражения нономино считаются различными, как это происходит с односторонними нономино, то первая и четвертая категории выше удваиваются в размере, что дает дополнительные 1215 нономино, что в сумме составляет 2500. Если вращения также считаются различными, то нономино из первой категории считаются восьмикратно, из следующих трех категорий считаются четырехкратно, из пятой категории считаются дважды, а из последней категории считаются только один раз. Это дает 1196 × 8 + (38+26+19) × 4 + 4 × 2 + 2 = 9910 фиксированных нономино.

Упаковка и укладка плитки

37 нономино имеют отверстия. ^[3]^[4] Следовательно, полный набор не может быть упакован в прямоугольник, и не все нономино имеют мозаику . Из 1285 свободных нономино 960 удовлетворяют критерию Конвея , а еще 88 могут образовать участок, удовлетворяющий этому критерию. Два дополнительных нономино допускают мозаику, но не удовлетворяют ни одному из предыдущих критериев. ^[5] Это самый низкий порядок полимино, для которого существуют такие исключения. ^[6]

У одного нономино есть отверстие размером в два квадрата (второе справа в верхнем ряду), и это самое маленькое полиомино с таким отверстием.

Ссылки

^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Princeton University Press. ISBN 0-691-02444-8.
^ ab Редельмейер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика . 36 : 191–203. doi : 10.1016/0012-365X(81)90237-5 .
^ Вайсштейн, Эрик В. «Полимино». Математический мир .
^ Слоан, Н. Дж. А. (ред.). "Последовательность A001419 (Число n-клеточных полимино с отверстиями)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
^ Rawsthorne, Daniel A. (1988). «Сложность замощения малых n-мино (n<10)». Дискретная математика . 70 : 71–75. doi : 10.1016/0012-365X(88)90081-7 .
^ Роадс, Гленн К. (2005). «Плоские мозаики полимино, полигексагонов и полиалмазов». Журнал вычислительной и прикладной математики . 174 (2): 329–353. doi :10.1016/j.cam.2004.05.002.

[1] Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Princeton University Press. ISBN 0-691-02444-8.

[Redelmeier-2] Редельмейер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика . 36 : 191–203. doi : 10.1016/0012-365X(81)90237-5 .

[3] Вайсштейн, Эрик В. «Полимино». Математический мир .

[4] Слоан, Н. Дж. А. (ред.). "Последовательность A001419 (Число n-клеточных полимино с отверстиями)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.

[5] Rawsthorne, Daniel A. (1988). «Сложность замощения малых n-мино (n<10)». Дискретная математика . 70 : 71–75. doi : 10.1016/0012-365X(88)90081-7 .

[6] Роадс, Гленн К. (2005). «Плоские мозаики полимино, полигексагонов и полиалмазов». Журнал вычислительной и прикладной математики . 174 (2): 329–353. doi :10.1016/j.cam.2004.05.002.