Рядом с наборами

В математике близкие множества являются либо пространственно близкими , либо описательно близкими. Пространственно близкие множества имеют непустое пересечение . Другими словами, пространственно близкие множества не являются непересекающимися множествами , поскольку они всегда имеют по крайней мере один общий элемент. Описательно близкие множества содержат элементы, которые имеют совпадающие описания. Такие множества могут быть либо непересекающимися, либо непересекающимися множествами. Пространственно близкие множества также являются описательно близкими множествами.

Базовое предположение с описательно близкими наборами заключается в том, что такие наборы содержат элементы, которые имеют местоположение и измеримые характеристики, такие как цвет и частота встречаемости. Описание элемента набора определяется вектором признаков . Сравнение векторов признаков обеспечивает основу для измерения близости описательно близких наборов. Теория близких наборов обеспечивает формальную основу для наблюдения, сравнения и классификации элементов в наборах на основе их близости, как пространственной, так и описательной. Близкие наборы предлагают структуру для решения проблем, основанных на человеческом восприятии , которые возникают в таких областях, как обработка изображений , компьютерное зрение , а также инженерные и научные проблемы.

Ближние множества имеют множество приложений в таких областях, как топология ^[37] , обнаружение и классификация образов ^[50] , абстрактная алгебра ^[51] , математика в информатике ^[38] и решение различных проблем, основанных на человеческом восприятии ^{[42] [82] [47] [52] [56],} которые возникают в таких областях, как анализ изображений ^{[54] [14] [46] [17] [18]} , обработка изображений ^[40] , распознавание лиц ^[13] , этология ^[64] , а также в инженерных и научных задачах ^{[55] [64] [42] [19] [17] [18]} . С самого начала описательно близкие множества оказались полезными в приложениях топологии ^[37] и визуального распознавания образов ^[50] , охватывая широкий спектр приложений, включая обнаружение камуфляжа , микропалеонтологию , обнаружение подделки почерка, биомедицинский анализ изображений, поиск изображений на основе содержания , динамику популяций , топологию фактора , текстильный дизайн , визуальный мерчандайзинг и топологическую психологию.

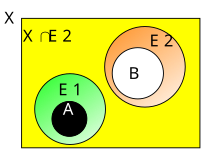
В качестве иллюстрации степени описательной близости между двумя наборами рассмотрим пример цветовой модели Генри для различных степеней близости между наборами элементов изображения на картинках (см., например , ^[17] §4.3). Две пары овалов на рис. 1 и рис. 2 содержат цветные сегменты. Каждый сегмент на рисунках соответствует классу эквивалентности, где все пиксели в классе имеют схожие описания, т. е . элементы изображения со схожими цветами. Овалы на рис. 1 ближе друг к другу описательно, чем овалы на рис. 2.

Было замечено, что простая концепция близости объединяет различные концепции топологических структур ^[20], поскольку категория Near всех пространств близости и отображений, сохраняющих близость, содержит категории sTop (симметричные топологические пространства и непрерывные отображения ^[3] ), Prox ( пространства близости и -отображения ^{[8] [67]} ), Unif ( равномерные пространства и равномерно непрерывные отображения ^{[81] [77]} ) и Cont (пространства смежности и отображения смежности ^[24] ) как вложенные полные подкатегории ^{[20] [59]} . Показано, что категории и являются полными суперкатегориями различных известных категорий, включая категорию симметричных топологических пространств и непрерывных отображений, а также категорию расширенных метрических пространств и нерасширяемых отображений. Обозначение гласит: категория вложена в категорию . Категории и являются суперкатегориями для множества знакомых категорий ^[76], показанных на рис. 3. Пусть обозначает категорию всех -приближенных пространств близости и сокращений, а пусть обозначает категорию всех -приближенных меротопических пространств и сокращений.${\displaystyle \дельта}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle {\boldsymbol {\varepsilon {AMer}}}}$${\displaystyle {\boldsymbol {sTop}}}$${\displaystyle {\boldsymbol {Met^{\infty }}}}$${\displaystyle {\boldsymbol {A}}\hookrightarrow {\boldsymbol {B}}}$ ${\displaystyle {\boldsymbol {A}}}$ ${\displaystyle {\boldsymbol {B}}}$${\displaystyle {\boldsymbol {\varepsilon AMer}}}$${\displaystyle {\boldsymbol {\varepsilon ANear}}}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle \varepsilon}$${\displaystyle {\boldsymbol {\varepsilon AMer}}}$${\displaystyle \varepsilon}$

Среди этих знакомых категорий есть , симметричная форма (см. категорию топологических пространств ), категория с объектами, которые являются топологическими пространствами, и морфизмами, которые являются непрерывными отображениями между ними ^{[1] [32]} . с объектами, которые являются расширенными метрическими пространствами, является подкатегорией (имеющей объекты - пространства сближения и сжатия) (см. также ^{[57] [75]} ). Пусть будут расширенными псевдометриками на непустых множествах , соответственно. Отображение является сжатием тогда и только тогда, когда является сжатием. Для непустых подмножеств функция расстояния определяется как${\displaystyle {\boldsymbol {sTop}}}$${\displaystyle {\boldsymbol {Top}}}$${\displaystyle {\boldsymbol {Met^{\infty }}}}$${\displaystyle {\boldsymbol {\varepsilon AP}}}$${\displaystyle \varepsilon}$${\displaystyle \rho _{X}, \rho _{Y}}$${\displaystyle X,Y}$${\displaystyle f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})}$${\displaystyle f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{\rho _{Y}}})}$${\displaystyle A,B\in 2^{X}}$${\displaystyle D_{\rho }:2^{X}\times 2^{X}\longrightarrow [0,\infty ]}$

${\displaystyle D_{\rho }(A,B)={\begin{cases}\inf {\{\rho (a,b):a\in A,b\in B\}},&{\text{if }}A{\text{ and }}B{\text{ are not empty}},\\\infty ,&{\text{if }}A{\text{ or }}B{\text{ is empty}}.\end{cases}}}$

Таким образом, AP вкладывается как полная подкатегория в функтором , определенным как и . Тогда является сжатием тогда и только тогда, когда является сжатием. Таким образом, вкладывается как полная подкатегория в функтором , определенным как и Поскольку категория расширенных метрических пространств и нерасширяемых отображений является полной подкатегорией , следовательно, является также полной суперкатегорией . Категория является топологической конструкцией ^[76] .${\displaystyle {\boldsymbol {\varepsilon }}}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle F((X,\rho ))=(X,\nu _{D_{\rho }})}$${\displaystyle F(f)=f}$${\displaystyle f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})}$${\displaystyle f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{\rho _{Y}}})}$${\displaystyle {\boldsymbol {\varepsilon {AP}}}}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle F((X,\rho ))=(X,\nu _{D_{\rho }})}$${\displaystyle F(f)=f.}$${\displaystyle {\boldsymbol {Met^{\infty }}}}$${\displaystyle {\boldsymbol {\varepsilon {AP}}}}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$${\displaystyle {\boldsymbol {Met^{\infty }}}}$${\displaystyle {\boldsymbol {\varepsilon {ANear}}}}$

Понятия близкого и далекого ^[A] в математике можно проследить до работ Иоганна Бенедикта Листинга и Феликса Хаусдорфа . Связанные с ними понятия сходства и подобия можно проследить до Дж. Х. Пуанкаре , который ввел наборы схожих ощущений (зарождающиеся классы толерантности) для представления результатов экспериментов Г. Т. Фехнера по чувствительности ощущений ^[10] и рамки для изучения сходства в представительных пространствах как моделей того, что он назвал физическими континуумами ^{[63] [60] [61]} . Элементами физического континуума (ФК) являются наборы ощущений. Понятие ПК и различных представительных пространств (тактильное, визуальное, моторное) были введены Пуанкаре в статье 1894 года о математическом континууме ^[63] , статье 1895 года о пространстве и геометрии ^[60] и краткой книге 1902 года о науке и гипотезах ^[61], за которыми последовал ряд разработок, например , ^[62] . Статьи 1893 и 1895 годов о континуумах (ч. 1, гл. II), а также представительных пространствах и геометрии (ч. 2, гл. IV) включены в качестве глав в ^[61] . Позднее Ф. Рисс ввел понятие близости или близости пар множеств на Международном конгрессе математиков (ICM) в 1908 году ^[65] .

В 1960-х годах EC Zeeman ввел пространства толерантности в моделирование зрительного восприятия ^[83] . AB Sossinsky заметил в 1986 году ^[71] , что основная идея, лежащая в основе теории пространств толерантности, исходит от Пуанкаре, особенно ^[60] . В 2002 году Z. Pawlak и J. Peters ^[B] рассмотрели неформальный подход к восприятию близости физических объектов, таких как снежинки, который не ограничивался пространственной близостью. В 2006 году формальный подход к описательной близости объектов был рассмотрен J. Peters, A. Skowron и J. Stepaniuk ^[C] в контексте пространств близости ^{[39] [33] [35] [21] . В 2007 году J. Peters [D] [E]} ввел описательно близкие множества, за которыми последовало введение множеств толерантности ^{[41] [45]} . В последнее время изучение описательно близких множеств привело к алгебраическим ^{[22] [51]} , топологическим и близостным пространственным ^[37] основам таких множеств.

Прилагательное «близкий» в контексте близких множеств используется для обозначения того факта, что наблюдаемые различия значений признаков отдельных объектов достаточно малы, чтобы считаться неразличимыми, т. е . находятся в пределах некоторого допуска.

Точная идея близости или «сходства» или «нахождения в пределах допуска» достаточно универсальна, чтобы вполне естественно появляться практически в любой математической обстановке (см., например , ^[66] ). Это особенно естественно в математических приложениях: практические задачи чаще всего имеют дело с приблизительными входными данными и требуют только жизнеспособных результатов с допустимым уровнем погрешности ^[71] .

Слова «близко» и «далеко» используются в повседневной жизни, и Ф. Рисс ^[65] высказал остроумное предложение сделать эти интуитивные концепции строгими. Он ввел концепцию близости пар множеств на ICM в Риме в 1908 году. Эта концепция полезна для упрощения преподавания исчисления и продвинутого исчисления. Например, переход от интуитивного определения непрерывности функции в точке к ее строгому определению эпсилон-дельта иногда бывает трудным для объяснения учителями и для понимания студентами. Интуитивно непрерывность можно объяснить с помощью языка близости, т. е . функция непрерывна в точке , при условии, что точки вблизи переходят в точки вблизи . Используя идею Рисса, это определение можно сделать более точным, и его контрапозитивом является известное определение ^{[4] [36]} .${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$${\displaystyle c}$${\displaystyle \{x\}}$${\displaystyle c}$${\displaystyle \{f(x)\}}$${\displaystyle f(c)}$

С пространственной точки зрения близость (также известная как близость) считается обобщением пересечения множеств . Для непересекающихся множеств форма пересечения множеств близости определяется в терминах набора объектов (извлеченных из непересекающихся множеств), которые имеют схожие черты в пределах некоторого допуска (см., например , §3 в ^[80] ). Например, овалы на рис. 1 считаются близкими друг к другу, поскольку эти овалы содержат пары классов, которые отображают схожие (визуально неразличимые) цвета.

Пусть обозначает метрическое топологическое пространство , наделенное одним или несколькими отношениями близости, а обозначим совокупность всех подмножеств . Совокупность называется множеством мощности .${\displaystyle X}$ ${\displaystyle 2^{X}}$${\displaystyle X}$${\displaystyle 2^{X}}$${\displaystyle X}$

Существует много способов определения близости Ефремовича в топологических пространствах (дискретная близость, стандартная близость, метрическая близость, близость Чеха, близость Александрова и близость Фрейденталя), Подробности см. в § 2, стр. 93–94 в ^[6] . Здесь основное внимание уделяется стандартной близости в топологическом пространстве. Для является близкой (обозначается как ), при условии, что их замыкания имеют общую точку.${\displaystyle A,B\subset X}$${\displaystyle A}$${\displaystyle B}$${\displaystyle A\ \delta \ B}$

Замыкание подмножества (обозначается как ) — это обычное замыкание Куратовского множества ^[F] , введенное в § 4, стр. 20 ^[27] , определяется как${\displaystyle A\in 2^{X}}$${\displaystyle {\mbox{cl}}(A)}$

${\displaystyle {\begin{aligned}{\mbox{cl}}(A)&=\left\{x\in X:D(x,A)=0\right\},\ {\mbox{where}}\\D(x,A)&=\inf \left\{d(x,a):a\in A\right\}.\end{aligned}}}$

То есть, есть множество всех точек в , которые близки к ( есть расстояние Хаусдорфа (см. § 22, стр. 128, в ^[15] ) между и множеством и (стандартное расстояние)). Стандартное отношение близости определяется как${\displaystyle {\mbox{cl}}(A)}$${\displaystyle x}$${\displaystyle X}$${\displaystyle A}$${\displaystyle D(x,A)}$${\displaystyle x}$${\displaystyle A}$${\displaystyle d(x,a)=\left|x-a\right|}$

${\displaystyle \delta =\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\ \cap \ {\mbox{cl}}(B)\neq \emptyset \right\}.}$

Если множества и не имеют общих точек, то они находятся далеко друг от друга (обозначается ).${\displaystyle A}$${\displaystyle B}$${\displaystyle A\ {\underline {\delta }}\ B}$

Следующие аксиомы пространства EF-близости ^[G] даны Юрием Михайловым Смирновым ^[67] на основе того, что ввел Вадим Арсеньевич Ефремович в первой половине 1930-х годов ^[8] . Пусть .${\displaystyle A,B,E\in 2^{X}}$

ЭФ.1

Если множество близко к , то близко к .${\displaystyle A}$${\displaystyle B}$${\displaystyle B}$${\displaystyle A}$

ЭФ.2

${\displaystyle A\cup B}$близко к , тогда и только тогда, когда хотя бы одно из множеств или близко к .${\displaystyle E}$${\displaystyle A}$${\displaystyle B}$${\displaystyle E}$

ЭФ.3

Две точки находятся близко тогда и только тогда, когда они являются одной и той же точкой.

ЭФ.4

Все множества далеки от пустого множества .${\displaystyle \emptyset }$

ЭФ.5

Для любых двух множеств и , которые далеки друг от друга, существует , , такое, что далеко от и далеко от ( аксиома Ефремовича ).${\displaystyle A}$${\displaystyle B}$${\displaystyle C,D\in 2^{X}}$${\displaystyle C\cup D=X}$${\displaystyle A}$${\displaystyle C}$${\displaystyle B}$${\displaystyle D}$

Пара называется пространством EF-близости . В этом контексте пространство — это множество с некоторой добавленной структурой. В пространстве близости структура индуцируется отношением EF-близости . В пространстве близости замыкание в совпадает с пересечением всех замкнутых множеств, содержащих .${\displaystyle (X,\delta )}$${\displaystyle X}$${\displaystyle X}$${\displaystyle \delta }$${\displaystyle X}$${\displaystyle A}$${\displaystyle X}$${\displaystyle A}$

Теорема 1 ^[67]

Замыкание любого множества в пространстве близости — это множество точек , которые близки к .${\displaystyle A}$${\displaystyle X}$${\displaystyle x\in X}$${\displaystyle A}$

Пусть множество представлено точками внутри прямоугольной области на рис. 5. Также пусть будут любыми двумя непересекающимися подмножествами ( т.е. подмножествами, пространственно далекими друг от друга) в , как показано на рис. 5. Пусть ( дополнение множества ). Тогда из аксиомы EF следует следующее:${\displaystyle X}$${\displaystyle A,B}$${\displaystyle X}$${\displaystyle C^{c}=X\backslash C}$${\displaystyle C}$

${\displaystyle {\begin{aligned}A&{}\mathrel {\underline {\delta }} B,\\B&\subset C,\\D&=C^{c},\\X&=D\cup C,\\A&\subset D,\ {\mbox{hence, we can write}}\\A\ {\underline {\delta }}\ B\ &\Rightarrow \ A\ {\underline {\delta }}\ C\ {\mbox{and}}\ B\ {\underline {\delta }}\ D,\ {\mbox{for some}}\ C,D\ {\mbox{in}}\ X{\mbox{ so that }}C\cup D=X.\qquad \blacksquare \end{aligned}}}$

Описательно близкие множества были введены как средство решения задач классификации и распознавания образов, возникающих из непересекающихся множеств, которые похожи друг на друга. ^{[44] [43]} Недавно связи между близкими множествами в EF-пространствах и близкими множествами в дескриптивных EF-пространствах были исследованы в. ^{[53] [48]}

Опять же, пусть будет метрическим топологическим пространством и пусть набор пробных функций, которые представляют особенности каждого . Сделанное здесь предположение содержит неабстрактные точки, которые имеют измеримые особенности, такие как ориентация градиента. Неабстрактная точка имеет местоположение и особенности, которые можно измерить (см. § 3 в ^[26] ).${\displaystyle X}$${\displaystyle \Phi =\left\{\phi _{1},\dots ,\phi _{n}\right\}}$${\displaystyle x\in X}$${\displaystyle X}$

Функция зонда представляет собой признак точки образца в . Отображение определяется как , где — n-мерное вещественное евклидово векторное пространство . — вектор признаков для , который обеспечивает описание . Например, это приводит к проксимальному представлению наборов точек изображения в цифровых изображениях. ^[48]${\displaystyle \phi :X\rightarrow \mathbb {R} }$${\displaystyle X}$${\displaystyle \Phi :X\longrightarrow \mathbb {R} ^{n}}$${\displaystyle \Phi (x)=(\phi _{1}(x),\dots ,\phi _{n}(x))}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \Phi (x)}$${\displaystyle x}$${\displaystyle x\in X}$

Чтобы получить описательное отношение близости (обозначаемое ), сначала выбирается набор функций зонда. Пусть будет отображением подмножества в подмножество . Например, пусть и обозначают наборы описаний точек в , соответственно. То есть,${\displaystyle \delta _{\Phi }}$${\displaystyle {\mathcal {Q}}:2^{X}\longrightarrow 2^{R^{n}}}$${\displaystyle 2^{X}}$${\displaystyle 2^{R^{n}}}$${\displaystyle A,B\in 2^{X}}$${\displaystyle {\mathcal {Q}}(A),{\mathcal {Q}}(B)}$${\displaystyle A,B}$

${\displaystyle {\begin{aligned}{\mathcal {Q}}(A)&=\left\{\Phi (a):a\in A\right\},\\{\mathcal {Q}}(B)&=\left\{\Phi (b):b\in B\right\}.\end{aligned}}}$

Выражение reads описательно близко . Аналогично, reads описательно далеко от . Описательная близость и определяется как${\displaystyle A\mathrel {\delta _{\Phi }} B}$${\displaystyle A}$ ${\displaystyle B}$${\displaystyle A\mathrel {{\underline {\delta }}_{\Phi }} B}$${\displaystyle A}$ ${\displaystyle B}$${\displaystyle A}$${\displaystyle B}$

${\displaystyle A\mathrel {\delta _{\Phi }} B\Leftrightarrow {\mathcal {Q}}({\mbox{cl}}(A))\mathrel {\delta } {\mathcal {Q}}({\mbox{cl}}(B))\neq \emptyset .}$

Описательное пересечение и определяется как${\displaystyle \mathop {\cap } _{\Phi }}$${\displaystyle A}$${\displaystyle B}$

${\displaystyle A\mathbin {\mathop {\cap } _{\Phi }} B=\left\{x\in A\cup B:{\mathcal {Q}}(A)\mathrel {\delta } {\mathcal {Q}}(B)\right\}.}$

То есть, находится в , при условии, что для некоторых . Заметьте, что и могут быть непересекающимися и при этом непустыми.${\displaystyle x\in A\cup B}$${\displaystyle A\mathbin {\mathop {\cap } _{\Phi }} B}$${\displaystyle \Phi (x)=\Phi (a)=\Phi (b)}$${\displaystyle a\in A,b\in B}$${\displaystyle A}$${\displaystyle B}$${\displaystyle A\mathbin {\mathop {\cap } _{\Phi }} B}$

Описательное отношение близости определяется как${\displaystyle \delta _{\Phi }}$

${\displaystyle \delta _{\Phi }=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\mathbin {\mathop {\cap } _{\Phi }} {\mbox{cl}}(B)\neq \emptyset \right\}.}$

Если множества и не имеют точек с совпадающими описаниями, то множества описательно далеки друг от друга (обозначается ).${\displaystyle A}$${\displaystyle B}$${\displaystyle A\ {\underline {\delta }}_{\Phi }\ B}$

Бинарное отношение является описательной EF-близостью , при условии, что для выполняются следующие аксиомы .${\displaystyle \delta _{\Phi }}$${\displaystyle A,B,E\subset X}$

деф.1

Если множество описательно близко к , то описательно близко к .${\displaystyle A}$${\displaystyle B}$${\displaystyle B}$${\displaystyle A}$

деф.2

${\displaystyle A\cup B}$описательно близок к , тогда и только тогда, когда хотя бы один из наборов или описательно близок к .${\displaystyle E}$${\displaystyle A}$${\displaystyle B}$${\displaystyle E}$

деф.3

Две точки описательно близки тогда и только тогда, когда описание совпадает с описанием .${\displaystyle x,y\in X}$${\displaystyle x}$${\displaystyle y}$

деф.4

Все непустые множества описательно далеки от пустого множества .${\displaystyle \emptyset }$

деф.5

Для любых двух множеств и , которые описательно далеки друг от друга, существует , , такое, что описательно далеко от и описательно далеко от ( описательная аксиома Ефремовича ).${\displaystyle A}$${\displaystyle B}$${\displaystyle C,D\in 2^{X}}$${\displaystyle C\cup D=X}$${\displaystyle A}$${\displaystyle C}$${\displaystyle B}$${\displaystyle D}$

Пара называется описательным пространством близости.${\displaystyle (X,\delta _{\Phi })}$

Релятор — это непустое семейство отношений на непустом множестве ^[72] . Пара (также обозначаемая ) называется пространством реляторов. Пространства реляторов являются естественными обобщениями упорядоченных множеств и равномерных пространств. ^{[73] [74]} С введением семейства отношений близости на мы получаем пространство проксимальных реляторов . Для простоты мы рассмотрим только два отношения близости, а именно близость Ефремовича ^[8] и дескриптивную близость при определении дескриптивного релятора . ^{[53] [48]} Пара называется пространством проксимальных реляторов ^[49] . В этой работе обозначает метрическое топологическое пространство, которое наделено отношениями в проксимальном реляторе. С введением традиционное замыкание подмножества (например, ^{[9] [7]} ) можно сравнить с более поздним дескриптивным замыканием подмножества.${\displaystyle {\mathcal {R}}}$${\displaystyle X}$${\displaystyle (X,{\mathcal {R}})}$${\displaystyle X({\mathcal {R}})}$${\displaystyle {\mathcal {R}}_{\delta }}$${\displaystyle X}$${\displaystyle (X,{\mathcal {R}}_{\delta })}$${\displaystyle \delta }$${\displaystyle \delta _{\Phi }}$ ${\displaystyle {\mathcal {R}}_{\delta _{\Phi }}}$${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi }})}$${\displaystyle X}$${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi }})}$

В пространстве проксимальных отношений дескриптивное замыкание множества (обозначаемое как ) определяется как${\displaystyle X}$ ${\displaystyle A}$${\displaystyle {\mbox{cl}}_{\Phi }(A)}$

${\displaystyle {\mbox{cl}}_{\Phi }(A)=\left\{x\in X:{\Phi (x)}\mathrel {\delta } {\mathcal {Q}}({\mbox{cl}}(A))\right\}.}$

То есть, находится в описательном замыкании , при условии, что замыкание и замыкание имеют хотя бы один общий элемент.${\displaystyle x\in X}$${\displaystyle A}$${\displaystyle \Phi (x)}$${\displaystyle {\mathcal {Q}}({\mbox{cl}}(A))}$

Теорема 2 ^[50]

Описательное замыкание любого множества в описательном пространстве EF-близости — это множество точек , которые описательно близки к .${\displaystyle A}$${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi }})}$${\displaystyle x\in X}$${\displaystyle A}$

Теорема 3 ^[50]

Замыкание Куратовского множества является подмножеством дескриптивного замыкания в дескриптивном пространстве EF-близости.${\displaystyle A}$${\displaystyle A}$

Теорема 4 ^[49]

Пусть — проксимальное реляционное пространство, Тогда .${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi }})}$${\displaystyle A\subset X}$${\displaystyle {\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)}$

Доказательство

Пусть такое, что для некоторого . Следовательно, . Отсюда,${\displaystyle \Phi (x)\in {\mathcal {Q}}(X\setminus {\mbox{cl}}(A))}$${\displaystyle \Phi (x)=\Phi (a)}$${\displaystyle a\in {\mbox{cl}}A}$${\displaystyle \Phi (x)\in {\mathcal {Q}}({\mbox{cl}}_{\Phi }(A))}$${\displaystyle {\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)}$

В пространстве проксимальных отношений EF-близость приводит к следующим результатам для описательной близости .${\displaystyle \delta }$${\displaystyle \delta _{\Phi }}$

Теорема 5 ^[49]

Пусть будет проксимальным реляторным пространством, Тогда${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi }})}$${\displaystyle A,B,C\subset X}$

1°

${\displaystyle A\ \delta \ B\ {\mbox{implies}}\ A\ \delta _{\Phi }\ B}$.

2°

${\displaystyle (A\cup B)\ \delta \ C\ {\mbox{implies}}\ (A\cup B)\ \delta _{\Phi }\ C}$.

3°

${\displaystyle {\mbox{cl}}A\ \delta \ {\mbox{cl}}B\ {\mbox{implies}}\ {\mbox{cl}}A\ \delta _{\Phi }\ {\mbox{cl}}B}$.

Доказательство

1°

${\displaystyle A\ \delta \ B\Leftrightarrow A\cap B\neq \emptyset }$. Для и . Следовательно, .${\displaystyle x\in A\cap B,\Phi (x)\in {\mathcal {Q}}(A)}$${\displaystyle \Phi (x)\in {\mathcal {Q}}(B)}$${\displaystyle A\ \delta _{\Phi }\ B}$

1° ⇒ 2°

3°

${\displaystyle {\mbox{cl}}A\ \delta \ {\mbox{cl}}B}$подразумевает, что и имеют хотя бы одну общую точку. Следовательно, 1° ⇒ 3°.${\displaystyle {\mbox{cl}}A}$${\displaystyle {\mbox{cl}}A}$

${\displaystyle \qquad \blacksquare }$

В псевдометрическом проксимальном пространстве отношений окрестность точки (обозначаемой ), для , определяется как${\displaystyle X}$${\displaystyle x\in X}$${\displaystyle N_{x,\varepsilon }}$${\displaystyle \varepsilon >0}$

${\displaystyle N_{x,\varepsilon }=\left\{y\in X:d(x,y)<\varepsilon \right\}.}$

Внутренность множества (обозначается как ) и граница (обозначается как ) в пространстве проксимальных отношений определяются как${\displaystyle A}$${\displaystyle {\mbox{int}}(A)}$${\displaystyle A}$${\displaystyle {\mbox{bdy}}(A)}$${\displaystyle X}$

${\displaystyle {\begin{aligned}{\mbox{int}}(A)&=\left\{x\in X:N_{x,\varepsilon }\subseteq A\right\}.\\{\mbox{bdy}}(A)&={\mbox{cl}}(A)\setminus {\mbox{int}}(A).\end{aligned}}}$

Множество имеет естественное сильное включение в множество, связанное с ^{[5] [6]} } (обозначается ), при условии ; т. е. ( далек от дополнения ). Соответственно, множество имеет описательное сильное включение в множество , связанное с (обозначается ), при условии ; т. е. ( далек от дополнения ).${\displaystyle A}$${\displaystyle B}$${\displaystyle \delta }$${\displaystyle A\ll _{\delta }B}$${\displaystyle A\subset {\mbox{int}}(B)}$${\displaystyle A\mathrel {\underline {\delta }} X\setminus {\mbox{int}}(B)}$${\displaystyle A}$${\displaystyle {\mbox{int}}(B)}$${\displaystyle A}$${\displaystyle B}$${\displaystyle \delta _{\Phi }}$${\displaystyle A\mathrel {\mathop {\ll } _{\Phi }} B}$${\displaystyle {\mathcal {Q}}(A)\subset \ {\mathcal {Q}}({\mbox{int}}(B))}$${\displaystyle A\ {\underline {\delta }}_{\Phi }\ X\setminus {\mbox{int}}(B)}$${\displaystyle {\mathcal {Q}}(A)}$${\displaystyle {\mbox{int}}B}$

Пусть будет описательным отношением соседства, определяемым как${\displaystyle \mathop {\ll } _{\Phi }}$${\displaystyle \delta }$

${\displaystyle \mathop {\ll } _{\Phi }=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mathcal {Q}}(A)\subset {\mathcal {Q}}({\mbox{int}}(B))\right\}.}$

То есть , при условии, что описание каждого содержится в наборе описаний точек . Теперь заметим, что любой в пространстве проксимальных отношений такой, что имеет непересекающиеся -окрестности; т.е.${\displaystyle A\mathrel {\mathop {\ll } _{\Phi }} B}$${\displaystyle a\in A}$${\displaystyle b\in {\mbox{int}}(B)}$${\displaystyle A,B}$${\displaystyle X}$${\displaystyle A\mathrel {{\underline {\delta }}_{\Phi }} B}$${\displaystyle \delta _{\Phi }}$

${\displaystyle A\mathrel {{\underline {\delta }}_{\Phi }} B\Leftrightarrow A\mathrel {\mathop {\ll } _{\Phi }} E1,B\mathrel {\mathop {\ll } _{\Phi }} E2,\ {\mbox{for some}}\ E1,E2\subset X\ {\mbox{(See Fig. 6).}}}$

Теорема 6 ^[50]

Любые два множества, описательно далекие друг от друга, принадлежат непересекающимся описательным -окрестностям в пространстве описательной близости .${\displaystyle \delta _{\Phi }}$${\displaystyle X}$

Рассмотрение сильного включения непустого множества в другое множество приводит к изучению топологий hit-and-miss и топологии Вайсмана. ^[2]

Пусть будет действительным числом больше нуля. При изучении множеств, которые являются проксимально близкими в пределах некоторого допуска, набор отношений близости дополняется псевдометрическим отношением близости толерантности (обозначаемым как ), определяемым как${\displaystyle \varepsilon }$${\displaystyle {\mathcal {R}}_{\delta _{\Phi }}}$${\displaystyle \delta _{\Phi ,\varepsilon }}$

${\displaystyle {\begin{aligned}D_{\Phi }(A,B)&=\inf \left\{d(\Phi (a),\Phi (a)):\Phi (a)\in {\mathcal {Q}}(A),\Phi (a)\in {\mathcal {Q}}(B)\right\},\\d(\Phi (a),\Phi (a))&=\mathop {\sum } _{i=1}^{n}|\phi _{i}(a)-\phi _{i}(b)|,\\\delta _{\Phi ,\varepsilon }&=\left\{(A,B)\in 2^{X}\times 2^{X}:|D({\mbox{cl}}(A),{\mbox{cl}}(B))|<\varepsilon \right\}.\end{aligned}}}$

Пусть . Другими словами, непустое множество, снабженное проксимальным релятором, имеет базовую структуру, предоставляемую проксимальным релятором , и обеспечивает основу для изучения толерантности около множеств в , которые близки в пределах некоторой толерантности. Множества в описательном псевдометрическом пространстве проксимального релятора являются толерантностью около множеств (т.е. ), при условии${\displaystyle {\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}={\mathcal {R}}_{\delta _{\Phi }}\cup \left\{\delta _{\Phi ,\varepsilon }\right\}}$${\displaystyle {\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}}$${\displaystyle {\mathcal {R}}_{\delta _{\Phi }}}$${\displaystyle X}$${\displaystyle A,B}$${\displaystyle (X,{\mathcal {R}}_{\delta _{\Phi ,\varepsilon }})}$${\displaystyle A\ \delta _{\Phi ,\varepsilon }\ B}$

${\displaystyle D_{\Phi }(A,B)<\varepsilon .}$

Отношения с теми же формальными свойствами, что и отношения подобия ощущений, рассмотренные Пуанкаре ^[62], в настоящее время, после Зеемана ^[83] , называются отношениями толерантности . Толерантность на множестве${\displaystyle \tau }$${\displaystyle O}$ — это отношение , которое является рефлексивным и симметричным. В алгебре термин отношение толерантности также используется в узком смысле для обозначения рефлексивных и симметричных отношений, определенных на универсумах алгебр, которые также совместимы с операциями данной алгебры, т. е . они являются обобщениями отношений конгруэнтности (см ., например , ^[12] ). При ссылке на такие отношения используется термин алгебраическая толерантность или термин алгебраическое отношение толерантности . Транзитивные отношения толерантности являются отношениями эквивалентности. Множество вместе с допуском называется пространством толерантности (обозначается ). Множество является -предклассом (или кратко предклассом , когда понимается) тогда и только тогда, когда для любого , .${\displaystyle \tau \subseteq O\times O}$${\displaystyle O}$${\displaystyle \tau }$${\displaystyle (O,\tau )}$${\displaystyle A\subseteq O}$${\displaystyle \tau }$${\displaystyle \tau }$${\displaystyle x,y\in A}$${\displaystyle (x,y)\in \tau }$

Семейство всех предклассов пространства толерантности естественным образом упорядочено по включению множеств, а предклассы, максимальные по включению множеств, называются -классами или просто классами , когда понимается . Семейство всех классов пространства особенно интересно и обозначается . Семейство является покрытием ^[58] .${\displaystyle \tau }$${\displaystyle \tau }$${\displaystyle (O,\tau )}$${\displaystyle H_{\tau }(O)}$${\displaystyle H_{\tau }(O)}$${\displaystyle O}$

Работа Пуанкаре и Зеемана по подобию предвещает введение близких множеств ^{[44] [43]} и исследования отношений подобия, например , ^[79] . В науке и технике толерантность близких множеств является практическим применением изучения множеств, которые близки в пределах некоторого допуска. Допуск напрямую связан с идеей близости или сходства ( т. е . нахождения в пределах некоторого допуска) при сравнении объектов. Путем применения подхода Пуанкаре к определению визуальных пространств и подхода Зеемана к отношениям толерантности основная идея заключается в сравнении объектов, таких как фрагменты изображения внутри цифровых изображений.${\displaystyle \varepsilon \in (0,\infty ]}$

Простой пример

Следующий простой пример демонстрирует построение классов толерантности из реальных данных. Рассмотрим 20 объектов в таблице ниже с .${\displaystyle |\Phi |=1}$

Образец системы восприятия

${\displaystyle x_{i}}$	${\displaystyle \phi (x)}$	${\displaystyle x_{i}}$	${\displaystyle \phi (x)}$	${\displaystyle x_{i}}$	${\displaystyle \phi (x)}$	${\displaystyle x_{i}}$	${\displaystyle \phi (x)}$
${\displaystyle x_{1}}$	.4518	${\displaystyle x_{6}}$	.6943	${\displaystyle x_{11}}$	.4002	${\displaystyle x_{16}}$	.6079
${\displaystyle x_{2}}$	.9166	${\displaystyle x_{7}}$	.9246	${\displaystyle x_{12}}$	.1910	${\displaystyle x_{17}}$	.1869
${\displaystyle x_{3}}$	.1398	${\displaystyle x_{8}}$	.3537	${\displaystyle x_{13}}$	.7476	${\displaystyle x_{18}}$	.8489
${\displaystyle x_{4}}$	.7972	${\displaystyle x_{9}}$	.4722	${\displaystyle x_{14}}$	.4990	${\displaystyle x_{19}}$	.9170
${\displaystyle x_{5}}$	.6281	${\displaystyle x_{10}}$	.4523	${\displaystyle x_{15}}$	.6289	${\displaystyle x_{20}}$	.7143

Пусть отношение толерантности определяется как

${\displaystyle \cong _{\varepsilon }{}\Leftrightarrow \{(x,y)\in O\times O:\;\parallel \Phi (x)-\Phi (y)\parallel _{_{2}}\leq \varepsilon \}}$

Затем настройка дает следующие классы допусков:${\displaystyle \varepsilon =0.1}$

${\displaystyle {\begin{aligned}H_{\cong _{\varepsilon }}(O)={}&\{\{x_{1},x_{8},x_{10},x_{11}\},\{x_{1},x_{9},x_{10},x_{11},x_{14}\},\\&\{x_{2},x_{7},x_{18},x_{19}\},\\&\{x_{3},x_{12},x_{17}\},\\&\{x_{4},x_{13},x_{20}\},\{x_{4},x_{18}\},\\&\{x_{5},x_{6},x_{15},x_{16}\},\{x_{5},x_{6},x_{15},x_{20}\},\\&\{x_{6},x_{13},x_{20}\}\}.\end{aligned}}}$

Обратите внимание, что каждый объект в классе толерантности удовлетворяет условию , и что почти все объекты появляются в более чем одном классе. Более того, если бы использовалось отношение неразличимости, было бы двадцать классов, поскольку нет двух объектов с совпадающими описаниями.${\displaystyle \parallel \Phi (x)-\Phi (y)\parallel _{2}\leq \varepsilon }$

Пример обработки изображения

Следующий пример представляет собой пример на основе цифровых изображений. Пусть подизображение определяется как небольшое подмножество пикселей, принадлежащих цифровому изображению, так что пиксели, содержащиеся в подизображении, образуют квадрат. Затем пусть наборы и соответственно представляют подизображения, полученные из двух разных изображений, и пусть . Наконец, пусть описание объекта дается компонентом Green в цветовой модели RGB . Следующий шаг — найти все классы допуска с использованием отношения допуска, определенного в предыдущем примере. Используя эту информацию, можно сформировать классы допуска, содержащие объекты, которые имеют схожие (в пределах некоторых небольших ) значения для компонента Green в цветовой модели RGB. Кроме того, изображения, которые близки (похожи) друг на друга, должны иметь классы допуска, разделенные между обоими изображениями (вместо классов допуска, содержащихся исключительно в одном из изображений). Например, на рисунке, сопровождающем этот пример, показано подмножество классов допуска, полученных из двух изображений листьев. На этом рисунке каждому классу допуска назначен отдельный цвет. Как можно видеть, два листа имеют схожие классы допуска. Этот пример подчеркивает необходимость измерения степени близости двух множеств.${\displaystyle X}$${\displaystyle Y}$${\displaystyle O=\{X\cup Y\}}$${\displaystyle \varepsilon }$

Пусть обозначает конкретное описательное псевдометрическое EF-проксимальное реляционное пространство, снабженное отношением близости и непустыми подмножествами , а также отношением толерантности, определенным в терминах набора зондов и с , где${\displaystyle (U,{\mathcal {R}}_{\delta _{\Phi ,\varepsilon }})}$${\displaystyle \delta _{\Phi ,\varepsilon }}$${\displaystyle X,Y\in 2^{U}}$${\displaystyle \cong _{\Phi ,\varepsilon }}$${\displaystyle \Phi }$${\displaystyle \varepsilon \in (0,\infty ]}$

${\displaystyle \simeq _{\Phi ,\varepsilon }=\{(x,y)\in U\times U\mid \ |\Phi (x)-\Phi (y)|\leq \varepsilon \}.}$

Далее предположим и пусть обозначает семейство всех классов в пространстве .${\displaystyle Z=X\cup Y}$${\displaystyle H_{\tau _{\Phi ,\varepsilon }}(Z)}$${\displaystyle (Z,\simeq _{\Phi ,\varepsilon })}$

Пусть . Расстояние определяется как${\displaystyle A\subseteq X,B\subseteq Y}$${\displaystyle D_{_{tNM}}:2^{U}\times 2^{U}:\longrightarrow [0,\infty ]}$

${\displaystyle D_{_{tNM}}(X,Y)={\begin{cases}1-tNM(A,B),&{\mbox{if }}X{\mbox{ and }}Y{\mbox{ are not empty}},\\\infty ,&{\mbox{if }}X{\mbox{ or }}Y{\mbox{ is empty}},\end{cases}}}$

где

${\displaystyle tNM(A,B)={\Biggl (}\sum _{C\in H_{\tau _{\Phi ,\varepsilon }}(Z)}|C|{\Biggr )}^{-1}\cdot \sum _{C\in H_{\tau _{\Phi ,\varepsilon }}(Z)}|C|{\frac {\min(|C\cap A|,|[C\cap B|)}{\max(|C\cap A|,|C\cap B|)}}.}$

Подробности приведены в ^{[14] [16] [17]} . Идея заключается в том, что наборы, которые похожи, должны иметь похожее количество объектов в каждом классе толерантности. Таким образом, для каждого класса толерантности, полученного из покрытия , подсчитывает количество объектов, которые принадлежат и , и берет отношение (как правильную дробь) их мощностей. Кроме того, каждое отношение взвешивается по общему размеру класса толерантности (тем самым придавая важность большим классам), а конечный результат нормализуется путем деления на сумму всех мощностей. Диапазон находится в интервале [0,1], где значение 1 получается, если наборы эквивалентны (на основе описаний объектов), а значение 0 получается, если у них нет общих описаний.${\displaystyle tNM}$${\displaystyle tNM}$${\displaystyle Z=X\cup Y}$${\displaystyle tNM}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle tNM}$

В качестве примера степени близости между двумя наборами рассмотрим рисунок ниже, на котором каждое изображение состоит из двух наборов объектов, и . Каждый цвет на рисунках соответствует набору, в котором все объекты в классе имеют одинаковое описание. Идея заключается в том, что близость наборов в перцептивной системе основана на мощности классов толерантности, которые они разделяют. Таким образом, наборы в левой части рисунка ближе (ближе) друг к другу с точки зрения их описаний, чем наборы в правой части рисунка.${\displaystyle X}$${\displaystyle Y}$${\displaystyle tNM}$

Система Near set Evaluation and Recognition (NEAR) — это система, разработанная для демонстрации практических приложений теории Near set к проблемам оценки сегментации изображений и соответствия изображений. Она была мотивирована потребностью в свободном программном инструменте, который может предоставлять результаты для исследований и вызывать интерес к теории Near set. Система реализует интерфейс нескольких документов (MDI), где каждая отдельная задача обработки выполняется в своем собственном дочернем кадре. Объекты (в смысле Near set) в этой системе являются подизображениями обрабатываемых изображений, а функции зонда (признаки) — это функции обработки изображений, определенные на подизображениях. Система была написана на языке C++ и была разработана для упрощения добавления новых задач обработки и функций зонда. В настоящее время система выполняет шесть основных задач, а именно: отображение классов эквивалентности и допуска для изображения, выполнение оценки сегментации, измерение близости двух изображений, выполнение поиска изображений на основе содержимого (CBIR) и отображение выходных данных обработки изображения с использованием определенной функции зонда.

Proximity System — это приложение, разработанное для демонстрации топологических подходов на основе описательных данных к близости и близости в контексте анализа цифровых изображений. Proximity System возникла из работы S. Naimpally и J. Peters по топологическим пространствам. Proximity System была написана на Java и предназначена для работы в двух различных операционных средах, а именно на смартфонах и планшетах Android, а также на настольных платформах, работающих под управлением Java Virtual Machine. Что касается настольной среды, Proximity System — это кроссплатформенное приложение Java для систем Windows, OSX и Linux, которое было протестировано на Windows 7 и Debian Linux с использованием Sun Java 6 Runtime. С точки зрения реализации теоретических подходов, как приложения для Android, так и настольные приложения используют одни и те же внутренние библиотеки для выполнения вычислений на основе описаний, где единственными отличиями являются пользовательский интерфейс, а версия Android имеет меньше доступных функций из-за ограничений на системные ресурсы.