Фактор момента инерции

В планетарных науках фактор момента инерции или нормализованный полярный момент инерции — безразмерная величина, характеризующая радиальное распределение массы внутри планеты или спутника . Поскольку момент инерции имеет размерность массы, умноженную на квадрат длины, фактор момента инерции — это коэффициент, который их умножает.

Определение

Для планетарного тела с главными моментами инерции фактор момента инерции определяется как А < Б < С {\displaystyle А<Б<В}

С М Р 2 {\displaystyle {\frac {C}{MR^{2}}}} ,

где C — первый главный момент инерции тела, M — масса тела, а R — средний радиус тела. [1] [2] Для сферы с однородной плотностью , . [примечание 1] [примечание 2] Для дифференцированной планеты или спутника, где плотность увеличивается с глубиной, . Величина является полезным индикатором наличия и протяженности планетарного ядра , поскольку большее отклонение от значения однородной плотности 2/5 передает большую степень концентрации плотных материалов по направлению к центру. С / М Р 2 = 2 / 5 {\displaystyle C/MR^{2}=2/5} С / М Р 2 < 2 / 5 {\displaystyle C/MR^{2}<2/5}

Ценности Солнечной системы

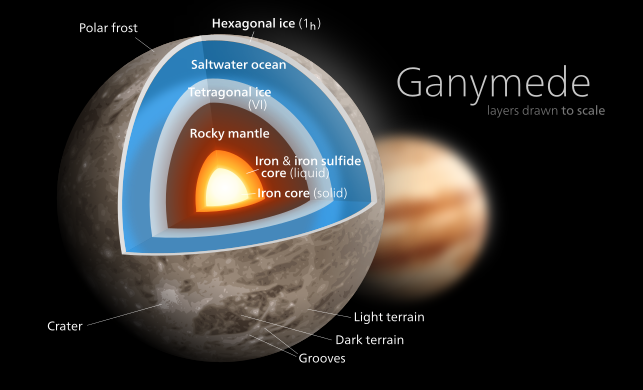
Солнце имеет самое низкое значение момента инерции среди тел Солнечной системы ; оно имеет самую высокую центральную плотность (162 г/см 3 , [3] [примечание 3] по сравнению с ~13 для Земли [4] [5] ) и относительно низкой средней плотностью (1,41 г/см 3 по сравнению с 5,5 для Земли). Сатурн имеет самое низкое значение среди газовых гигантов отчасти потому, что у него самая низкая объемная плотность (0,687 г/см3 ) . [6] Ганимед имеет самый низкий момент инерции среди твердых тел в Солнечной системе из-за его полностью дифференцированной внутренней части, [7] [8] в результате частичного приливного нагрева из-за резонанса Лапласа , [9] а также его существенного компонента водяного льда низкой плотности . Каллисто похож по размеру и объемному составу на Ганимед, но не является частью орбитального резонанса и менее дифференцирован. [7] [8] Считается , что у Луны небольшое ядро, но ее внутренняя часть в остальном относительно однородна. [10] [11]

ТелоЦенитьИсточникПримечания
Солнце0,070[3]Не измерено
Меркурий0,346 ± 0,014[12]
Венера0,337 ± 0,024[13]
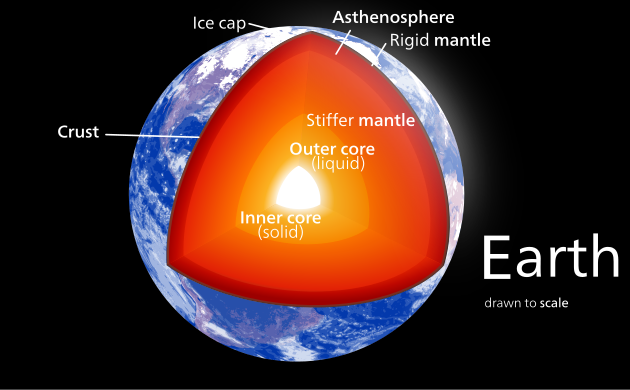
Земля0,3307[14]
Луна0,3929 ± 0,0009[15]
Марс0,3644 ± 0,0005[16]
Церера0,36 ± 0,15 [примечание 4][18]Не измерено (диапазон отражает различные предположения относительно исходной скорости вращения [18] )
Юпитер0,2756 ± 0,0006[19]Не измерено (расчеты двухслойной модели ограничены данными гравитации Juno [19] )
Ио0,37824 ± 0,00022[20]Не измерено (соотношение Дарвина-Радо)
Европа0,346 ± 0,005[20]Не измерено (соотношение Дарвина-Радо)
Ганимед0,3115 ± 0,0028[20]Не измерено (соотношение Дарвина-Радо)
Каллисто0,3549 ± 0,0042[20]Не измерено (соотношение Дарвина-Радо)
Сатурн0,22[21]Не измерено (соотношение Дарвина-Радо)
Энцелад0,3305 ± 0,0025[22]Не измерено (соотношение Дарвина-Радо)
Рея0,3911 ± 0,0045[23]Не измерено (соотношение Дарвина-Радо)
Титан0,341[24]Не измерено (соотношение Дарвина-Радо)
Уран0,23[25]Не измерено (приближенное решение уравнения Клеро)
Нептун0,23[25]Не измерено (приближенное решение уравнения Клеро)

Измерение

Полярный момент инерции традиционно определяется путем объединения измерений спиновых величин ( скорость прецессии спина и/или наклон ) с гравитационными величинами (коэффициентами сферического гармонического представления гравитационного поля). Для сбора этих геодезических данных обычно требуется орбитальный космический аппарат .

Приближение

Для тел, находящихся в гидростатическом равновесии , соотношение Дарвина-Радо может обеспечить оценку фактора момента инерции на основе величин формы, спина и гравитации. [26]

Роль в моделях интерьера

Фактор момента инерции обеспечивает важное ограничение для моделей, представляющих внутреннюю структуру планеты или спутника. Как минимум, приемлемые модели профиля плотности должны соответствовать объемной плотности массы и фактору момента инерции тела.

Примечания

  1. ^ Для сферы с однородной плотностью мы можем вычислить момент инерции и массу, проинтегрировав по дискам от "южного полюса" до "северного полюса". Используя плотность 1, диск радиуса r имеет момент инерции
    ∫ 0 г 2 π г 3   г г = π г 4 2 {\displaystyle \int _{0}^{r}2\пи r^{3}\ dr={\frac {\пи r^{4}}{2}}}
    в то время как масса
    ∫ 0 г 2 π г   г г = π г 2 {\displaystyle \int _{0}^{r}2\пи r\ dr=\пи r^{2}}
    Проинтегрировав и умножив, получим: г = Р потому что ⁡ θ {\displaystyle r=R\cos \theta } Р грех ⁡ θ {\displaystyle R\sin \theta }
    С Р 5 = π 2 ∫ − 1 1 потому что 4 ⁡ θ   г грех ⁡ θ = π 2 ∫ − 1 1 ( 1 − грех 2 ⁡ θ ) 2   г грех ⁡ θ = π 2 ∫ − 1 1 ( 1 − 2 грех 2 ⁡ θ + грех 4 ⁡ θ ) г грех ⁡ θ = π 2 ∫ − 1 1 ( г грех ⁡ θ − 2 3 г грех 3 ⁡ θ + 1 5 г грех 5 ⁡ θ ) = 8 15 π {\displaystyle {\begin{aligned}{\frac {C}{R^{5}}}&={\frac {\pi }{2}}\int _{-1}^{1}\cos ^{4}\theta \ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-\sin ^{2}\theta )^{2}\ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-2\sin ^{2}\theta +\sin ^{4}\theta )d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(d\sin \theta -{\frac {2}{3}}d\sin ^{3}\theta +{\frac {1}{5}}d\sin ^{5}\theta )\\&={\frac {8}{15}}\pi \end{align}}}
    М Р 3 = π ∫ − 1 1 потому что 2 ⁡ θ   г грех ⁡ θ = π ∫ − 1 1 ( 1 − грех 2 ⁡ θ ) г грех ⁡ θ = π ∫ − 1 1 ( г грех ⁡ θ − 1 3 г грех 3 ⁡ θ ) = 4 3 π {\displaystyle {\begin{align}{\frac {M}{R^{3}}}&=\pi \int _{-1}^{1}\cos ^{2}\theta \ d\sin \theta \\&=\pi \int _{-1}^{1}(1-\sin ^{2}\theta )d\sin \theta \\&=\pi \int _{-1}^{1}(d\sin \theta -{\frac {1}{3}}d\sin ^{3}\theta )\\&={\frac {4}{3}}\pi \end{align}}}
    Это дает . С / М Р 2 = 2 / 5 {\displaystyle C/MR^{2}=2/5}
  2. ^ Для нескольких других примеров (в которых ось вращения является осью симметрии, если не указано иное) сплошной конус имеет коэффициент 3/10; однородный тонкий стержень (вращающийся вокруг своего центра перпендикулярно своей оси, так что R — это длина/2) имеет коэффициент 1/3; полый конус или сплошной цилиндр имеют коэффициент 1/2; полая сфера имеет коэффициент 2/3; полый открытый цилиндр имеет коэффициент 1.
  3. ^ Центральная плотность звезды имеет тенденцию увеличиваться в течение ее жизни , за исключением кратковременных событий ядерного синтеза в ядре, таких как гелиевая вспышка .
  4. ^ Значение, указанное для Цереры, представляет собой средний момент инерции, который, как полагают, лучше отражает ее внутреннюю структуру, чем полярный момент инерции, из-за ее высокой полярной сплющенности. [17]

Ссылки

  1. ^ Хаббард, Уильям Б. (1984). Планетарные интерьеры . Нью-Йорк, Нью-Йорк: Van Nostrand Reinhold. ISBN 978-0442237042. OCLC  10147326.
  2. ^ де Патер, Имке; Лиссауэр, Джек Дж. (2015). Планетарные науки (2-е обновленное издание). Нью-Йорк: Cambridge University Press . ISBN 978-0521853712. OCLC  903194732.
  3. ^ ab Williams, DR "Sun Fact Sheet". Planetary Fact Sheets . NASA . Получено 26.01.2017 .
  4. ^ Робертсон, Юджин С. (26 июля 2001 г.). «Внутренняя часть Земли». USGS . Получено 24 марта 2007 г.
  5. ^ Хазлетт, Джеймс С.; Монро, Рид; Викандер, Ричард (2006). Физическая геология: исследование Земли (6-е изд.). Belmont: Thomson. стр. 346. ISBN 9780495011484.
  6. ^ Уильямс, Дэвид Р. (7 сентября 2006 г.). "Saturn Fact Sheet". NASA . Архивировано из оригинала 14 апреля 2014 г. Получено 31 июля 2007 г.
  7. ^ ab Showman, Adam P.; Malhotra, Renu (1999-10-01). "Галилеевы спутники" (PDF) . Science . 286 (5437): 77–84. doi :10.1126/science.286.5437.77. PMID  10506564.
  8. ^ ab Sohl, F.; Spohn, T; Breuer, D.; Nagel, K. (2002). «Выводы из наблюдений Галилея о внутренней структуре и химии галилеевых спутников». Icarus . 157 (1): 104–119. Bibcode :2002Icar..157..104S. doi :10.1006/icar.2002.6828.
  9. ^ Шоумен, Адам П.; Стивенсон, Дэвид Дж.; Малхотра, Рену (1997). «Связанная орбитальная и тепловая эволюция Ганимеда» (PDF) . Icarus . 129 (2): 367–383. Bibcode : 1997Icar..129..367S. doi : 10.1006/icar.1997.5778.
  10. ^ Браун, Д.; Андерсон, Дж. (6 января 2011 г.). «Исследовательская группа НАСА обнаружила, что у Луны есть ядро, похожее на земное». НАСА . НАСА .
  11. ^ Вебер, RC; Лин, П.-Й.; Гарнеро, Э.Дж.; Уильямс, К.; Логнонн, П. (2011-01-21). "Сейсмическое обнаружение лунного ядра" (PDF) . Наука . 331 (6015): 309–312. Bibcode :2011Sci...331..309W. doi :10.1126/science.1199375. PMID  21212323. S2CID  206530647. Архивировано из оригинала (PDF) 2015-10-15 . Получено 2017-04-10 .
  12. ^ Марго, Жан-Люк; Пил, Стэнтон Дж.; Соломон, Шон К.; Хаук, Стивен А.; Гиго, Фрэнк Д.; Юргенс, Рэймонд Ф.; Изебудт, Мари; Джорджини, Джон Д.; Падован, Себастьяно; Кэмпбелл, Дональд Б. (2012). «Момент инерции Меркурия по данным о вращении и гравитации». Журнал геофизических исследований: Планеты . 117 (E12): E00L09–. Bibcode : 2012JGRE..117.0L09M. doi : 10.1029/2012JE004161 . ISSN  0148-0227.
  13. ^ Марго, Жан-Люк; Кэмпбелл, Дональд Б.; Джорджини, Джон Д.; Джао, Джозеф С.; Снедекер, Лоуренс Г.; Гиго, Фрэнк Д.; Бонсолл, Эмбер (29 апреля 2021 г.). «Спиновое состояние и момент инерции Венеры». Природная астрономия . 5 (7): 676–683. arXiv : 2103.01504 . Бибкод : 2021NatAs...5..676M. дои : 10.1038/s41550-021-01339-7. ISSN  2397-3366. S2CID  232092194.
  14. ^ Уильямс, Джеймс Г. (1994). «Вклад в скорость наклона, прецессию и нутацию Земли». The Astronomical Journal . 108 : 711. Bibcode : 1994AJ....108..711W. doi : 10.1086/117108 . ISSN  0004-6256. S2CID  122370108.
  15. ^ Уильямс, Джеймс Г.; Ньюхолл, XX; Дики, Джин О. (1996). «Лунные моменты, приливы, ориентация и системы координат». Планетная и космическая наука . 44 (10): 1077–1080. Bibcode : 1996P&SS...44.1077W. doi : 10.1016/0032-0633(95)00154-9. ISSN  0032-0633.
  16. ^ Konopliv, Alex S.; Asmar, Sami W.; Folkner, William M.; Karatekin, Özgür; Nunes, Daniel C.; Smrekar, Suzanne E.; Yoder, Charles F.; Zuber, Maria T. (январь 2011 г.). «Марсианские гравитационные поля высокого разрешения от MRO, сезонная гравитация Марса и другие динамические параметры». Icarus . 211 (1): 401–428. Bibcode :2011Icar..211..401K. doi :10.1016/j.icarus.2010.10.004.
  17. ^ Park, RS; Konopliv, AS; Bills, BG; Rambaux, N.; Castillo-Rogez, JC; Raymond, CA; Vaughan, AT; Ermakov, AI; Zuber, MT; Fu, RR; Toplis, MJ; Russell, CT; Nathues, A.; Preusker, F. (2016-08-03). "Частично дифференцированная внутренняя часть для (1) Ceres, выведенная из ее гравитационного поля и формы". Nature . 537 (7621): 515–517. Bibcode :2016Natur.537..515P. doi :10.1038/nature18955. PMID  27487219. S2CID  4459985.
  18. ^ ab Mao, X.; McKinnon, WB (2018). «Более быстрый палеоспин и глубоко залегающая нескомпенсированная масса как возможные объяснения современной формы и гравитации Цереры». Icarus . 299 : 430–442. Bibcode :2018Icar..299..430M. doi :10.1016/j.icarus.2017.08.033.
  19. ^ ab Ni, D. (2018). "Эмпирические модели недр Юпитера по данным Juno". Астрономия и астрофизика . 613 : A32. doi : 10.1051/0004-6361/201732183 .
  20. ^ abcd Шуберт, Г.; Андерсон, Дж. Д.; Спон, Т.; Маккиннон, У. Б. (2004). «Внутренний состав, структура и динамика галилеевых спутников». В Багенал, Ф.; Доулинг, ТЕ; Маккиннон, У. Б. (ред.). Юпитер: планета, спутники и магнитосфера. Нью-Йорк: Cambridge University Press. С. 281–306. ISBN 978-0521035453. OCLC  54081598.
  21. ^ Fortney, JJ; Helled, R.; Nettlemann, N.; Stevenson, DJ; Marley, MS; Hubbard, WB; Iess, L. (6 декабря 2018 г.). «Внутренняя часть Сатурна». В Baines, KH; Flasar, FM; Krupp, N.; Stallard, T. (ред.). Saturn in the 21st Century . Cambridge University Press. стр. 44–68. ISBN 978-1-108-68393-7.
  22. ^ МакКиннон, У. Б. (2015). «Влияние быстрого синхронного вращения Энцелада на интерпретацию гравитации Кассини». Geophysical Research Letters . 42 (7): 2137–2143. Bibcode : 2015GeoRL..42.2137M. doi : 10.1002/2015GL063384 .
  23. ^ Андерсон, Дж. Д.; Шуберт, Г. (2007). «Спутник Сатурна Рея представляет собой однородную смесь камня и льда». Geophysical Research Letters . 34 (2): L02202. Bibcode : 2007GeoRL..34.2202A. doi : 10.1029/2006GL028100. S2CID  128410558.
  24. ^ Дюранте, Д.; Хемингуэй, ДЖ.; Рачиоппа, П.; Иесс, Л.; Стивенсон, ДЖ. (2019). «Гравитационное поле Титана и внутренняя структура после Кассини» (PDF) . Икар . 326 : 123–132. Bibcode :2019Icar..326..123D. doi :10.1016/j.icarus.2019.03.003. hdl : 11573/1281269 . S2CID  127984873.
  25. ^ ab Yoder, C. (1995). Ahrens, T. (ред.). Астрометрические и геодезические свойства Земли и Солнечной системы. Вашингтон, округ Колумбия: AGU. ISBN 978-0-87590-851-9. OCLC  703657999. Архивировано из оригинала 2016-03-04 . Получено 2016-08-19 .
  26. ^ Мюррей, Карл Д.; Дермотт, Стэнли Ф. (13 февраля 2000 г.). Динамика солнечной системы. Кембридж: Cambridge University Press. ISBN 978-1139936156. OCLC  40857034.
Взято с "https://en.wikipedia.org/w/index.php?title=Момент_инерции_фактора&oldid=1201742624"