Модуль
Вычислительная операция

В вычислениях операция деления по модулю возвращает остаток или знаковый остаток от деления после деления одного числа на другое, называемый модулем операции.

Для двух положительных чисел a и n , модуль n (часто сокращенно a mod n ) является остатком от евклидова деления числа a на n , где a — делимое , а n — делитель . [1]

Например, выражение «5 mod 2» даст результат 1, поскольку 5 при делении на 2 даст частное 2 и остаток 1, тогда как выражение «9 mod 3» даст результат 0, поскольку 9 при делении на 3 даст частное 3 и остаток 0.

Хотя обычно выполняется с a и n , оба являющимися целыми числами , многие вычислительные системы теперь допускают другие типы числовых операндов. Диапазон значений для операции целочисленного модуля n составляет от 0 до n − 1 ( mod 1 всегда равен 0; mod 0 не определен, поскольку является делением на ноль ).

Когда хотя бы одно из чисел a или n отрицательно, базовое определение нарушается, и языки программирования различаются в том, как определяются эти значения.

Варианты определения

В математике результатом операции по модулю является класс эквивалентности , и любой член класса может быть выбран в качестве представителя ; однако, обычным представителем является наименьший положительный остаток , наименьшее неотрицательное целое число, принадлежащее этому классу (т. е. остаток от евклидова деления ). [2] Однако возможны и другие соглашения. Компьютеры и калькуляторы имеют различные способы хранения и представления чисел; таким образом, их определение операции по модулю зависит от языка программирования или базового оборудования .

Почти во всех вычислительных системах частное q и остаток r от деления a на n удовлетворяют следующим условиям:

д ∈ З а = н д + г | г | < | н | {\displaystyle {\begin{align}&q\in \mathbb {Z} \\&a=nq+r\\&|r|<|n|\end{align}}} ( 1 )

Это все еще оставляет неоднозначность знака, если остаток не равен нулю: возможны два варианта для остатка, один отрицательный, а другой положительный; этот выбор определяет, какой из двух последовательных частных должен использоваться для удовлетворения уравнения (1). В теории чисел всегда выбирается положительный остаток, но в вычислениях языки программирования выбирают в зависимости от языка и знаков a или n . [a] Например, стандартный Паскаль и АЛГОЛ 68 дают положительный остаток (или 0) даже для отрицательных делителей, а некоторые языки программирования, такие как C90, оставляют это на усмотрение реализации, когда либо n , либо a отрицательны (подробнее см. таблицу в разделе Языки программирования). a по модулю 0 не определено в большинстве систем, хотя некоторые определяют его как a .

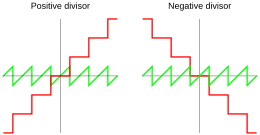
  •  Частное ( q ) и остаток ( r ) как функция делимого ( a ), используя усеченное деление

    Во многих реализациях используется усеченное деление , для которого частное определяется как

    д = ствол ⁡ ( а н ) {\displaystyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}

    где - функция целой части ( округление к нулю ), т.е. усечение до нулевых значащих цифр. Таким образом, согласно уравнению ( 1 ), остаток имеет тот же знак, что и делимое a, поэтому может принимать 2| n | − 1 значений: ствол {\displaystyle \operatorname {trunc} }

    г = а − н ствол ⁡ ( а н ) {\displaystyle r=an\operatorname {trunc} \left({\frac {a}{n}}\right)}
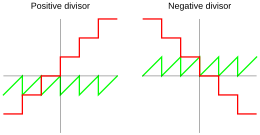
  • Частное и остаток с использованием дробного деления

    Дональд Кнут [3] продвигает метод деления с минимальным дроблением , для которого частное определяется как

    д = ⌊ а н ⌋ {\displaystyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }

    где - функция пола ( округление вниз ). Таким образом, согласно уравнению ( 1 ), остаток имеет тот же знак, что и делитель n : ⌊ ⌋ {\displaystyle \lfloor \,\rfloor }

    г = а − н ⌊ а н ⌋ {\displaystyle r=an\left\lfloor {\frac {a}{n}}\right\rfloor }
  • Частное и остаток с использованием евклидова деления

    Рэймонд Т. Бут [4] продвигает евклидово деление , для которого частное определяется как

    д = знак ⁡ ( н ) ⌊ а | н | ⌋ = { ⌊ а н ⌋ если  н > 0 ⌈ а н ⌉ если  н < 0 {\displaystyle q=\operatorname {sgn}(n)\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor ={\begin{cases}\left\lfloor {\frac {a}{n}}\right\rfloor &{\text{if }}n>0\\\left\lceil {\frac {a}{n}}\right\rceil &{\text{if }}n<0\\\end{cases}}}

    где sgn — функция знака , — функция пола ( округление вниз ), а — функция потолка ( округление вверх ). Таким образом, согласно уравнению ( 1 ), остаток неотрицателен : ⌊ ⌋ {\displaystyle \lfloor \,\rfloor } ⌈ ⌉ {\ displaystyle \ lceil \, \ rceil }

    г = а − | н | ⌊ а | н | ⌋ {\displaystyle r=a-|n|\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor }
  • Частное и остаток с использованием округленного деления

    Common Lisp и IEEE 754 используют округленное деление , для которого частное определяется как

    д = круглый ⁡ ( а н ) {\displaystyle q=\operatorname {round} \left({\frac {a}{n}}\right)}

    где round — функция округления ( округление половины до четного ). Таким образом, согласно уравнению ( 1 ), остаток попадает между и , а его знак зависит от того, с какой стороны от нуля он попадает в эти границы: − н 2 {\displaystyle -{\frac {n}{2}}} н 2 {\displaystyle {\frac {n}{2}}}

    г = а − н круглый ⁡ ( а н ) {\displaystyle r=an\operatorname {round} \left({\frac {a}{n}}\right)}
  • Частное и остаток с использованием деления на вершину

    Common Lisp также использует деление по потолку , для которого частное определяется как

    д = ⌈ а н ⌉ {\displaystyle q=\left\lceil {\frac {a}{n}}\right\rceil }

    где ⌈⌉ — функция потолка ( округление вверх ). Таким образом, согласно уравнению ( 1 ), остаток имеет противоположный знак делителя :

    г = а − н ⌈ а н ⌉ {\displaystyle r=an\left\lceil {\frac {a}{n}}\right\rceil }

Если и делимое, и делитель положительны, то усеченное, уменьшенное и евклидово определения согласуются. Если делимое положительно, а делитель отрицателен, то усеченное и евклидово определения согласуются. Если делимое отрицательно, а делитель положительный, то усеченное и евклидово определения согласуются. Если и делимое, и делитель отрицательны, то усеченное и уменьшенное определения согласуются.

Как описывает Лейен,

Бут утверждает, что евклидово деление превосходит другие с точки зрения регулярности и полезных математических свойств, хотя floored delegate, продвигаемое Кнутом, также является хорошим определением. Несмотря на его широкое использование, усеченное деление, как показано, уступает другим определениям.

—  Даан Лейен, «Деление и модуль для компьютерных ученых» [5]

Однако усеченное деление удовлетворяет тождеству . [6] ( − а ) / б = − ( а / б ) = а / ( − б ) {\displaystyle ({-a})/b={-(a/b)}=a/({-b})}

Обозначение

Некоторые калькуляторы имеют кнопку функции mod() , и многие языки программирования имеют похожую функцию, например, mod( a , n ) . Некоторые также поддерживают выражения, которые используют "%", "mod" или "Mod" в качестве оператора остатка или модуля , например a % nили a mod n.

Для сред, в которых отсутствует подобная функция, можно использовать любое из трех приведенных выше определений.

Распространенные ошибки

Когда результат операции по модулю имеет знак делимого (усеченное определение), это может привести к неожиданным ошибкам.

Например, чтобы проверить, является ли целое число нечетным , можно попробовать проверить, равен ли остаток от деления на 2 1:

bool is_odd ( int n ) { return n % 2 == 1 ; }

Но в языке, где modulo имеет знак делимого, это неверно, потому что когда n (делимое) отрицательно и нечетно, n mod 2 возвращает −1, а функция возвращает false.

Правильным вариантом является проверка того, что остаток не равен 0 (поскольку остаток 0 одинаков независимо от знаков):

bool is_odd ( int n ) { return n % 2 != 0 ; }

Проблемы с производительностью

Операции по модулю могут быть реализованы таким образом, что деление с остатком вычисляется каждый раз. Для особых случаев на некоторых аппаратных средствах существуют более быстрые альтернативы. Например, модуль степеней 2 может быть альтернативно выражен как побитовая операция И (предполагая, что x — положительное целое число, или используя необрезающее определение):

x % 2n == x & (2n - 1)

Примеры:

x % 2 == x & 1
x % 4 == x & 3
x % 8 == x & 7

В устройствах и программном обеспечении, которые реализуют побитовые операции более эффективно, чем по модулю, эти альтернативные формы могут привести к более быстрым вычислениям. [7]

Оптимизации компилятора могут распознавать выражения вида expression % constant, где constantявляется степенью двойки, и автоматически реализовывать их как expression & (constant-1), позволяя программисту писать более понятный код без ущерба для производительности. Эта простая оптимизация невозможна для языков, в которых результат операции по модулю имеет знак делимого (включая C ), если только делимое не является целочисленным типом без знака . Это связано с тем, что если делимое отрицательно, то и модуль будет отрицательным, тогда как expression & (constant-1)всегда будет положительным. Для этих языков вместо этого необходимо использовать эквивалентность, выраженную с помощью побитовых операций ИЛИ, НЕ и И.x % 2n == x < 0 ? x | ~(2n - 1) : x & (2n - 1)

Существуют также оптимизации для общих операций с постоянным модулем, в которых сначала вычисляется деление с использованием оптимизации с постоянным делителем .

Свойства (идентичности)

Некоторые операции по модулю могут быть факторизованы или расширены аналогично другим математическим операциям. Это может быть полезно в криптографических доказательствах, таких как обмен ключами Диффи–Хеллмана . Свойства, включающие умножение, деление и возведение в степень, обычно требуют, чтобы a и n были целыми числами.

В языках программирования

Операторы по модулю в различных языках программирования
ЯзыкОператорЦелое числоС плавающей точкойОпределение
АБАПMODДаДаЕвклидов
ActionScript%ДаНетУсеченный
АдаmodДаНетНапольный [8]
remДаНетУсеченный [8]
АЛГОЛ 68÷×,modДаНетЕвклидов
АМПЛmodДаНетУсеченный
АПЛ|[б]ДаДаНапольный
AppleScriptmodДаНетУсеченный
АвтоЛИСП(rem d n)ДаНетУсеченный
АВК%ДаНетУсеченный
Баш%ДаНетУсеченный
БАЗОВЫЙModДаНетЗависит от реализации
до нашей эры%ДаНетУсеченный
С
С++		%,divДаНетУсеченный [c]
fmod(С)
std::fmod(С++)		НетДаУсеченный [11]
remainder(С)
std::remainder(С++)		НетДаОкруглый
С#%ДаДаУсеченный
Math.IEEERemainderНетДаОкруглый [12]
Кларион%ДаНетУсеченный
ЧистыйremДаНетУсеченный
КложурmodДаНетНапольный [13]
remДаНетУсеченный [14]
КОБОЛFUNCTION MODДаНетНапольный [15]
FUNCTION REMДаДаУсеченный [15]
CoffeeScript%ДаНетУсеченный
%%ДаНетНапольный [16]
Холодный фьюжн%,MODДаНетУсеченный
Общий промежуточный языкrem(подпись)ДаДаУсеченный [17]
rem.un(без подписи)ДаНет—
Общий ЛиспmodДаДаНапольный
remДаДаУсеченный
Кристалл%,moduloДаДаНапольный
remainderДаДаУсеченный
CSSmod()ДаДаНапольный [18]
rem()ДаДаУсеченный [19]
Д%ДаДаУсеченный [20]
Дарт%ДаДаЕвклидово [21]
remainder()ДаДаУсеченный [22]
Эйфелева\\ДаНетУсеченный
Эликсирrem/2ДаНетУсеченный [23]
Integer.mod/2ДаНетНапольный [24]
ВязmodByДаНетНапольный [25]
remainderByДаНетУсеченный [26]
ЭрлангremДаНетУсеченный
math:fmod/2НетДаУсеченный (то же, что и C) [27]
ЭйфорияmodДаНетНапольный
remainderДаНетУсеченный
Фа#%ДаДаУсеченный
Math.IEEERemainderНетДаОкруглый [12]
ФакторmodДаНетУсеченный
ФайлмейкерModДаНетНапольный
ВпередmodДаНетРеализация определена
fm/modДаНетНапольный
sm/remДаНетУсеченный
ФортранmodДаДаУсеченный
moduloДаДаНапольный
ФринкmodДаНетНапольный
Полный БАЗОВЫЙMODДаДаНапольный [28]
REMAINDERДаДаУсеченный [29]
ГЛСЛ%ДаНетНе определено [30]
modНетДаНапольный [31]
Студия GameMaker (GML)mod,%ДаНетУсеченный
GDScript (Годо)%ДаНетУсеченный
fmodНетДаУсеченный
posmodДаНетЕвклидов
fposmodНетДаЕвклидов
Идти%ДаНетУсеченный [32]
math.ModНетДаУсеченный [33]
big.Int.ModДаНетЕвклидово [34]
big.Int.RemДаНетУсеченный [35]
Круто%ДаНетУсеченный
ХаскеллmodДаНетНапольный [36]
remДаНетУсеченный [36]
Data.Fixed.mod'( ГХК )НетДаНапольный
Хаксе%ДаНетУсеченный
HLSL%ДаДаНе определено [37]
Дж.|[б]ДаНетНапольный
Ява%ДаДаУсеченный
Math.floorModДаНетНапольный
JavaScript
TypeScript		%ДаДаУсеченный
ДжулияmodДаДаНапольный [38]
%,remДаДаУсеченный [39]
Котлин%,remДаДаУсеченный [40]
modДаДаНапольный [41]
кш%ДаНетУсеченный (то же, что и POSIX sh)
fmodНетДаУсеченный
LabVIEWmodДаДаУсеченный
LibreOffice=MOD()ДаНетНапольный
ЛоготипMODULOДаНетНапольный
REMAINDERДаНетУсеченный
Луа 5%ДаДаНапольный
Луа 4mod(x,y)ДаДаУсеченный
Свобода БАЗОВЫЙMODДаНетУсеченный
Маткадmod(x,y)ДаНетНапольный
Кленe mod m(по умолчанию),modp(e, m)ДаНетЕвклидов
mods(e, m)ДаНетОкруглый
frem(e, m)ДаДаОкруглый
МатематикаMod[a, b]ДаНетНапольный
МАТЛАБmodДаНетНапольный
remДаНетУсеченный
МаксимаmodДаНетНапольный
remainderДаНетУсеченный
Встроенный язык Maya%ДаНетУсеченный
Майкрософт Эксель=MOD()ДаДаНапольный
МинитабMODДаНетНапольный
Модула-2MODДаНетНапольный
REMДаНетУсеченный
свинка#ДаНетНапольный
Сетевой ассемблер ( NASM , NASMX )%, div(без подписи)ДаНет—
%%(подпись)ДаНетОпределено реализацией [42]
НимmodДаНетУсеченный
ОберонMODДаНетНапольный [d]
Objective-C%ДаНетУсеченный (то же, что и C99)
Объект Паскаль , ДельфиmodДаНетУсеченный
OCamlmodДаНетУсеченный [43]
mod_floatНетДаУсеченный [44]
Оккам\ДаНетУсеченный
Паскаль (ISO-7185 и -10206)modДаНетЕвклидовоподобный [e]
Перл%ДаНетНапольный [ж]
POSIX::fmodНетДаУсеченный
ФиксmodДаНетНапольный
remainderДаНетУсеченный
PHP%ДаНетУсеченный [46]
fmodНетДаУсеченный [47]
PIC БАЗОВЫЙ ПРО\\ДаНетУсеченный
ПЛ/ИmodДаНетНапольный (ANSI PL/I)
PowerShell%ДаНетУсеченный
Программный код ( PRC )MATH.OP - 'MOD; (\)'ДаНетНеопределенный
ПрогрессmoduloДаНетУсеченный
Пролог (ИСО 1995)modДаНетНапольный
remДаНетУсеченный
ЧистыйБазовый%,Mod(x,y)ДаНетУсеченный
ЧистыйСкрипт`mod`ДаНетЕвклидово [48]
Чистые данные%ДаНетУсеченный (то же, что и C)
modДаНетНапольный
Питон%ДаДаНапольный
math.fmodНетДаУсеченный
math.remainderНетДаОкруглый
Вопрос №%ДаНетУсеченный [49]
Р%%ДаДаНапольный [50]
РакеткаmoduloДаНетНапольный
remainderДаНетУсеченный
Раку%НетДаНапольный
RealBasicMODДаНетУсеченный
ПричинаmodДаНетУсеченный
Рекс//ДаДаУсеченный
РПГ%REMДаНетУсеченный
Рубин%,modulo()ДаДаНапольный
remainder()ДаДаУсеченный
Ржавчина%ДаДаУсеченный
rem_euclid()ДаДаЕвклидово [51]
САСMODДаНетУсеченный
Скала%ДаДаУсеченный
СхемаmoduloДаНетНапольный
remainderДаНетУсеченный
Схема Р 6 РСmodДаНетЕвклидово [52]
mod0ДаНетОкруглый [52]
flmodНетДаЕвклидов
flmod0НетДаОкруглый
ЦарапатьmodДаДаНапольный
Семя7modДаДаНапольный
remДаДаУсеченный
SenseTalkmoduloДаНетНапольный
remДаНетУсеченный
sh(POSIX) (включая bash , mksh и т. д.)%ДаНетУсеченный (то же, что и C) [53]
Smalltalk\\ДаНетНапольный
rem:ДаНетУсеченный
Щелчок!modДаНетНапольный
Вращаться//ДаНетНапольный
Прочность%ДаНетУсеченный [54]
SQL ( SQL:1999 )mod(x,y)ДаНетУсеченный
SQL ( SQL:2011 )%ДаНетУсеченный
Стандартный МЛmodДаНетНапольный
Int.remДаНетУсеченный
Real.remНетДаУсеченный
Статаmod(x,y)ДаНетЕвклидов
Быстрый%ДаНетУсеченный [55]
remainder(dividingBy:)НетДаОкруглый [56]
truncatingRemainder(dividingBy:)НетДаУсеченный [57]
Тсл%ДаНетНапольный
fmod()НетДаУсеченный (как C)
тчш%ДаНетУсеченный
Крутящий момент%ДаНетУсеченный
ТьюрингmodДаНетНапольный
Верилог (2001)%ДаНетУсеченный
VHDLmodДаНетНапольный
remДаНетУсеченный
ВимЛ%ДаНетУсеченный
Визуальный базовыйModДаНетУсеченный
Веб-сборкаi32.rem_u, i64.rem_u(без подписи)ДаНет— [58]
i32.rem_s, i64.rem_s(подпись)ДаНетУсеченный [58]
x86 сборкаIDIVДаНетУсеченный
XBase++%ДаДаУсеченный
Mod()ДаДаНапольный
Зиг%,

@mod,@rem

ДаДаУсеченный [59]
Доказательство теоремы Z3div,modДаНетЕвклидов

Кроме того, многие компьютерные системы предоставляют divmodфункционал, который производит частное и остаток одновременно. Примерами служат инструкция архитектуры x86IDIV , функция языка программирования C div()и функция Pythondivmod() .

Обобщения

Модуль со смещением

Иногда полезно, чтобы результат деления по модулю n лежал не между 0 и n − 1 , а между некоторым числом d и d + n − 1. В этом случае d называется смещением , а d = 1 встречается особенно часто.

Похоже, что для этой операции не существует стандартной нотации, поэтому давайте предварительно будем использовать a mod d n . Таким образом, у нас есть следующее определение: [60] x = a mod d n на всякий случай d ≤ x ≤ d + n − 1 и x mod n = a mod n . Очевидно, что обычная операция по модулю соответствует нулевому смещению: a mod n = a mod 0 n .

Операция по модулю со смещением связана с функцией пола следующим образом:

а мод г ⁡ н = а − н ⌊ а − г н ⌋ . {\displaystyle a\operatorname {mod} _{d}n=an\left\lfloor {\frac {ad}{n}}\right\rfloor .}

Чтобы увидеть это, пусть . Сначала покажем, что x mod n = a mod n . В общем случае верно, что ( a + bn ) mod n = a mod n для всех целых чисел b ; таким образом, это верно и в частном случае, когда ; но это означает, что , что мы и хотели доказать. Осталось показать, что d ≤ x ≤ d + n − 1 . Пусть k и r — целые числа, такие что a − d = kn + r с 0 ≤ r ≤ n − 1 (см. Евклидово деление ). Тогда , таким образом . Теперь возьмем 0 ≤ r ≤ n − 1 и прибавим d к обеим сторонам, получив d ≤ d + r ≤ d + n − 1 . Но мы видели, что x = d + r , так что мы закончили. х = а − н ⌊ а − г н ⌋ {\textstyle x=an\left\lfloor {\frac {ad}{n}}\right\rfloor } б = − ⌊ а − г н ⌋ {\textstyle b=-\!\left\lfloor {\frac {ad}{n}}\right\rfloor } х мод н = ( а − н ⌊ а − г н ⌋ ) мод н = а мод н {\textstyle x{\bmod {n}}=\left(an\left\lfloor {\frac {ad}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\ бмод {n}}} ⌊ а − г н ⌋ = к {\textstyle \left\lfloor {\frac {ad}{n}}\right\rfloor =k} х = а − н ⌊ а − г н ⌋ = а − н к = г + г {\textstyle x=an\left\lfloor {\frac {ad}{n}}\right\rfloor =a-nk=d+r}

Модуль со смещением a mod d n реализован в Mathematica как Mod[a, n, d] . [60]

Реализация других определений по модулю с использованием усечения

Несмотря на математическую элегантность деления Кнута и евклидова деления, в языках программирования обычно гораздо чаще встречается усеченное деление по модулю. Лейен предоставляет следующие алгоритмы для вычисления двух делений, заданных усеченным целочисленным делением: [5]

/* Евклидов и Floored divmod, в стиле ldiv() языка C */ typedef struct { /* Эта структура является частью C stdlib.h, но воспроизведена здесь для ясности */ long int quot ; long int rem ; } ldiv_t ;          /* Евклидово деление */ inline ldiv_t ldivE ( long numer , long denom ) { /* Языки C99 и C++11 определяют оба эти метода как усечение. */ long q = numer / denom ; long r = numer % denom ; if ( r < 0 ) { if ( denom > 0 ) { q = q - 1 ; r = r + denom ; } else { q = q + 1 ; r = r - denom ; } } return ( ldiv_t ){. quot = q , . rem = r }; }                                                             /* Деление с меньшим числом */ inline ldiv_t ldivF ( long numer , long denom ) { long q = numer / denom ; long r = numer % denom ; if (( r > 0 && denom < 0 ) || ( r < 0 && denom > 0 )) { q = q - 1 ; r = r + denom ; } return ( ldiv_t ){. quot = q , . rem = r }; }

Для обоих случаев остаток можно вычислить независимо от частного, но не наоборот. Операции здесь объединены для экономии места на экране, поскольку логические ветви одинаковы.

Смотрите также

Примечания

  1. ^ Математически эти два варианта являются всего лишь двумя из бесконечного числа вариантов, доступных для неравенства, которому удовлетворяет остаток .
  2. ^ ab Порядок аргументов меняет местами, т.е. α|ωвычисляет остаток при делении на . ω мод α {\displaystyle \omega {\bmod {\alpha }}} ωα
  3. ^ C99 и C++11 определяют поведение, которое %должно быть усечено. [9] Стандарты до этого момента оставляли поведение, определяемое реализацией. [10]
  4. ^ Делитель должен быть положительным, в противном случае не определен.
  5. ^ Как обсуждал Буте, определения ISO Pascal для divи modне подчиняются тождеству деления D = d · ( D / d ) + D  % d и, таким образом, в корне нарушены.
  6. ^ Perl обычно использует арифметический оператор по модулю, который не зависит от машины. Примеры и исключения см. в документации Perl по мультипликативным операторам. [45]

Ссылки

  1. ^ Weisstein, Eric W. "Конгруэнтность". Wolfram MathWorld . Получено 27.08.2020 .
  2. ^ Колдуэлл, Крис. "остаток". Prime Glossary . Получено 27 августа 2020 г.
  3. ^ Кнут, Дональд Э. (1972). Искусство программирования . Эддисон-Уэсли.
  4. ^ Boute, Raymond T. (апрель 1992 г.). «Евклидово определение функций div и mod». ACM Transactions on Programming Languages ​​and Systems . 14 (2). ACM Press (Нью-Йорк, штат Нью-Йорк, США): 127–144. doi :10.1145/128861.128862. hdl : 1854/LU-314490 . S2CID  8321674.
  5. ^ ab Leijen, Daan (3 декабря 2001 г.). «Деление и модуль для компьютерных ученых» (PDF) . Microsoft . Получено 25.12.2014 .
  6. ^ Peterson, Doctor (5 июля 2001 г.). "Mod Function and Negative Numbers". Math Forum - Ask Dr. Math . Архивировано из оригинала 2019-10-22 . Получено 22 октября 2019 г.
  7. ^ Хорват, Адам (5 июля 2012 г.). «Более быстрое деление и операция по модулю — сила двойки».
  8. ^ ab ISO/IEC 8652:2012 - Информационные технологии — Языки программирования — Ada . ISO , IEC . 2012. раздел 4.5.5 Операторы умножения.
  9. ^ "Спецификация C99 (ISO/IEC 9899:TC2)" (PDF) . 2005-05-06. раздел 6.5.5 Мультипликативные операторы . Получено 16 августа 2018 г. .
  10. ^ ISO/IEC 14882:2003: Языки программирования – C++ . Международная организация по стандартизации (ISO), Международная электротехническая комиссия (IEC). 2003. раздел 5.6.4. бинарный оператор % возвращает остаток от деления первого выражения на второе. .... Если оба операнда неотрицательны, то остаток неотрицателен; в противном случае знак остатка определяется реализацией.
  11. ^ ISO/IEC 9899:1990: Языки программирования – C. ISO , IEC . 1990. раздел 7.5.6.4. Функция fmod возвращает значение x - i * y для некоторого целого числа i, такого, что если y не равен нулю, результат имеет тот же знак, что и x , и величину, меньшую величины y .
  12. ^ ab dotnet-bot. "Math.IEEERemainder(Double, Double) Method (System)". Microsoft Learn . Получено 2022-10-04 .
  13. ^ "clojure.core - Документация API Clojure v1.10.3". clojure.github.io . Получено 2022-03-16 .
  14. ^ "clojure.core - Документация API Clojure v1.10.3". clojure.github.io . Получено 2022-03-16 .
  15. ^ ab ISO/IEC JTC 1/SC 22/WG 4 (январь 2023 г.). ISO/IEC 1989:2023 – Язык программирования COBOL . ISO .{{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )
  16. ^ Операторы CoffeeScript
  17. ^ ISO/IEC JTC 1/SC 22 (февраль 2012 г.). ISO/IEC 23271:2012 — Информационные технологии — Инфраструктура общего языка (CLI). ISO . §§ III.3.55–56.{{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )
  18. ^ "mod() - CSS: каскадные таблицы стилей | MDN". developer.mozilla.org . 2024-06-22 . Получено 2024-10-23 .
  19. ^ "rem() - CSS: каскадные таблицы стилей | MDN". developer.mozilla.org . 2024-10-15 . Получено 2024-10-23 .
  20. ^ "Выражения - Язык программирования D". dlang.org . Получено 2021-06-01 .
  21. ^ "operator % method - num class - dart:core library - Dart API". api.dart.dev . Получено 2021-06-01 .
  22. ^ "метод остатка - класс num - библиотека dart:core - Dart API". api.dart.dev . Получено 01.06.2021 .
  23. ^ "Ядро — Elixir v1.11.3". hexdocs.pm . Получено 28.01.2021 .
  24. ^ "Integer — Elixir v1.11.3". hexdocs.pm . Получено 2021-01-28 .
  25. ^ "Basics - core 1.0.5". package.elm-lang.org . Получено 2022-03-16 .
  26. ^ "Basics - core 1.0.5". package.elm-lang.org . Получено 2022-03-16 .
  27. ^ "Erlang -- math". erlang.org . Получено 2021-06-01 .
  28. ^ ANSI (28 января 1987 г.). Языки программирования — Полный BASIC. Нью-Йорк: Американский национальный институт стандартов. § 5.4.4. X по модулю Y, т. е. XY*INT(X/Y).
  29. ^ ANSI (28 января 1987 г.). Языки программирования — Полный BASIC. Нью-Йорк: Американский национальный институт стандартов. § 5.4.4. Функция остатка, т. е. XY*IP(X/Y).
  30. ^ "GLSL Language Specification, Version 4.50.7" (PDF) . раздел 5.9 Выражения. Если оба операнда неотрицательны, то остаток неотрицателен. Результаты не определены, если один или оба операнда отрицательны.
  31. ^ «Спецификация языка GLSL, версия 4.50.7» (PDF) . раздел 8.3 Общие функции.
  32. ^ "Спецификация языка программирования Go - Язык программирования Go". go.dev . Получено 28.02.2022 .
  33. ^ "math package - math - pkg.go.dev". pkg.go.dev . Получено 28.02.2022 .
  34. ^ "большой пакет - math/big - pkg.go.dev". pkg.go.dev . Получено 28.02.2022 .
  35. ^ "большой пакет - math/big - pkg.go.dev". pkg.go.dev . Получено 2024-04-12 .
  36. ^ ab "6 предопределенных типов и классов". www.haskell.org . Получено 2022-05-22 .
  37. ^ "Операторы". Microsoft . 30 июня 2021 г. . Получено 2021-07-19 . Оператор % определен только в случаях, когда обе стороны положительны или обе стороны отрицательны. В отличие от C, он также работает с типами данных с плавающей точкой, а также с целыми числами.
  38. ^ "Математика · Язык Julia". docs.julialang.org . Получено 20.11.2021 .
  39. ^ "Математика · Язык Julia". docs.julialang.org . Получено 20.11.2021 .
  40. ^ "rem - Язык программирования Kotlin". Kotlin . Получено 2021-05-05 .
  41. ^ "mod - Язык программирования Kotlin". Kotlin . Получено 2021-05-05 .
  42. ^ "Глава 3: Язык NASM". NASM - Netwide Assembler версии 2.15.05 .
  43. ^ "Библиотека OCaml: Stdlib". ocaml.org . Получено 2022-02-19 .
  44. ^ "Библиотека OCaml: Stdlib". ocaml.org . Получено 2022-02-19 .
  45. ^ Документация Perl
  46. ^ "PHP: Арифметические операторы - Руководство". www.php.net . Получено 20.11.2021 .
  47. ^ "PHP: fmod - Руководство". www.php.net . Получено 2021-11-20 .
  48. ^ "Евклидово кольцо".
  49. ^ QuantumWriter. "Выражения". docs.microsoft.com . Получено 11 июля 2018 г. .
  50. ^ "R: Арифметические операторы". search.r-project.org . Получено 2022-12-24 .
  51. ^ "F32 - Ржавчина".
  52. ^ ab r6rs.org
  53. ^ "Shell Command Language". pubs.opengroup.org . Получено 2021-02-05 .
  54. ^ "Документация Solidity". docs.soliditylang.org . Получено 2024-10-17 .
  55. ^ "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
  56. ^ "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
  57. ^ "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
  58. ^ ab Rossberg, Andreas, ed. (19 апреля 2022 г.). «Спецификация ядра WebAssembly: версия 2.0». Консорциум World Wide Web . § 4.3.2 Целочисленные операции.
  59. ^ "Документация Zig". Язык программирования Zig . Получено 2022-12-18 .
  60. ^ ab "Mod". Wolfram Language & System Documentation Center . Wolfram Research . 2020. Получено 8 апреля 2020 г.
  • Различные виды целочисленного деления
  • Modulorama, анимация циклического представления таблиц умножения (объяснение на французском)
Взято с "https://en.wikipedia.org/w/index.php?title=Modulo&oldid=1252852268"