Очистка (фармакология)
В фармакологии клиренс ( ) — это фармакокинетический параметр, представляющий эффективность выведения лекарственного средства. Это скорость выведения вещества, деленная на его концентрацию. [ 1] Параметр также указывает теоретический объем плазмы , из которого вещество будет полностью удалено за единицу времени. Обычно клиренс измеряется в л/ч или мл/мин. [2] Экскреция , с другой стороны, является измерением количества вещества, удаляемого из организма за единицу времени (например, мг/мин, мкг/мин и т. д.). Хотя клиренс и выведение вещества связаны, это не одно и то же. Концепция клиренса была описана Томасом Аддисом , выпускником Медицинской школы Эдинбургского университета .
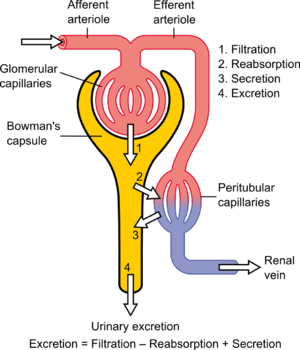
Вещества в организме могут выводиться различными органами, включая почки, печень, легкие и т. д. Таким образом, общий клиренс организма равен сумме клиренса вещества каждым органом (например, почечный клиренс + печеночный клиренс + легочный клиренс = общий клиренс организма). Однако для многих лекарств клиренс является исключительно функцией почечной экскреции. В этих случаях клиренс почти синонимичен почечному клиренсу или почечному плазменному клиренсу . Каждое вещество имеет определенный клиренс, который зависит от того, как вещество обрабатывается нефроном. Клиренс является функцией 1) клубочковой фильтрации , 2) секреции из перитубулярных капилляров в нефрон и 3) реабсорбции из нефрона обратно в перитубулярные капилляры . Клиренс является переменной величиной в кинетике нулевого порядка , поскольку постоянное количество препарата выводится за единицу времени, но он постоянен в кинетике первого порядка , поскольку количество препарата, выведенного за единицу времени, изменяется в зависимости от концентрации препарата в крови. [3] [4]
Клиренс может относиться к объему плазмы, из которой вещество удаляется (т.е. очищается ) за единицу времени или, в некоторых случаях, межкомпонентный клиренс может обсуждаться, когда речь идет о перераспределении между такими компартментами организма, как плазма, мышцы и жир. [2]
Определение
Клиренс вещества – это объем плазмы, содержащий такое же количество вещества, которое было удалено из плазмы за единицу времени. [5] : 228
Применительно к функции почек клиренс считается количеством жидкости, отфильтрованной из крови, которая обрабатывается почками , или количеством крови, очищенной за единицу времени, поскольку он имеет единицы объемного расхода [ объем за единицу времени ]. Однако он не относится к реальному значению; «почка не полностью удаляет вещество из общего потока почечной плазмы». [6] С точки зрения массопереноса [7] и физиологически объемный кровоток (к диализному аппарату и/или почке) является лишь одним из нескольких факторов, которые определяют концентрацию крови и выведение вещества из организма. Другие факторы включают коэффициент массопереноса , поток диализата и поток рециркуляции диализата для гемодиализа, а также скорость клубочковой фильтрации и скорость канальцевой реабсорбции для почек. Физиологическая интерпретация клиренса (в устойчивом состоянии) заключается в том, что клиренс представляет собой отношение образования массы и концентрации крови (или плазмы ) .
Его определение следует из дифференциального уравнения , описывающего экспоненциальный спад и используемого для моделирования функции почек и работы аппарата гемодиализа :
| 1 |
Где:
- скорость образования массы вещества - предполагается постоянной, т.е. не зависящей от времени (равной нулю для экзогенных (чужеродных) веществ/лекарств) [ммоль/мин] или [моль/с]
- t — время диализа или время с момента инъекции вещества/препарата [мин] или [с]
- V — объем распределения или общего объема воды в организме [л] или [м 3 ]
- K — клиренс [мл/мин] или [м 3 /с]
- C — концентрация [ммоль/л] или [моль/м 3 ] (в США часто [мг/мл])
Из приведенных выше определений следует, что — первая производная концентрации по времени, т.е. изменение концентрации со временем.
Он выводится из баланса масс.
Выведение вещества иногда выражается как обратная величина постоянной времени , описывающей скорость его выведения из организма, деленная на объем его распределения (или общее количество воды в организме).
В стационарном состоянии он определяется как скорость образования массы вещества (которая равна скорости удаления массы), деленная на его концентрацию в крови .
Клиренс, период полувыведения и объем распределения
Существует важная связь между клиренсом, периодом полувыведения и объемом распределения. Константа скорости выведения препарата эквивалентна общему клиренсу, деленному на объем распределения.
(обратите внимание на использование Cl, а не Κ, чтобы не путать с ). Но также эквивалентно делению на скорость выведения период полувыведения , . Таким образом, . Это означает, например, что увеличение общего клиренса приводит к уменьшению скорости выведения период полувыведения, при условии, что объем распределения постоянен. [8]
Эффект связывания с белками плазмы
Для веществ, которые демонстрируют существенное связывание с белками плазмы , клиренс обычно зависит от общей концентрации (свободная + связанная с белками), а не от свободной концентрации. [9]
Большинство плазменных веществ в первую очередь регулируют свои свободные концентрации, которые, таким образом, остаются прежними, поэтому обширное связывание с белками увеличивает общую концентрацию в плазме (свободные + связанные с белками). Это снижает клиренс по сравнению с тем, что было бы в случае, если бы вещество не связывалось с белками. [9] Однако скорость удаления массы та же самая, [9] поскольку она зависит только от концентрации свободного вещества и не зависит от связывания с белками плазмы, даже с учетом того факта, что плазменные белки увеличивают свою концентрацию в дистальном почечном клубочке , поскольку плазма фильтруется в капсулу Боумена, поскольку относительное увеличение концентраций вещества-белка и незанятого белка равнозначно и, следовательно, не дает чистого связывания или диссоциации веществ от плазменных белков, тем самым обеспечивая постоянную плазменную концентрацию свободного вещества по всей гломеруле, что также имело бы место без какого-либо связывания с белками плазмы.
Однако в других местах, помимо почек, где клиренс осуществляется мембранными транспортными белками, а не фильтрацией, обширное связывание с белками плазмы может увеличивать клиренс, поддерживая концентрацию свободного вещества на достаточно постоянном уровне по всему капиллярному руслу, препятствуя снижению клиренса, вызванному снижением концентрации свободного вещества через капилляры.
Вывод уравнения
Уравнение 1 выведено из баланса масс :
| 2 |
где:
- это период времени
- изменение массы токсина в организме во время
- это скорость поступления токсинов
- скорость удаления токсинов
- скорость образования токсинов
На словах приведенное выше уравнение гласит:
- Изменение массы токсина в организме ( ) в течение некоторого времени равно поступлению токсина плюс образованию токсина минус выведение токсина.
С
| 3 |
и
| 4 |
Уравнение A1 можно переписать как:
| 5 |
Если объединить in и gen вместе, т.е. и разделить на результат, то получится разностное уравнение :
| 6 |
Если применить предел, то получится дифференциальное уравнение:
| 7 |
Используя правило произведения, это можно переписать так:
| 8 |
Если предположить, что изменение объема незначительно, т.е. , то результатом будет Уравнение 1 :
Решение дифференциального уравнения
Общее решение приведенного выше дифференциального уравнения (1) имеет вид: [10] [11]
| 9 |
Где:
- C o – концентрация в начале диализа или начальная концентрация вещества/препарата (после его распределения) [ммоль/л] или [моль/м 3 ]
- e — основание натурального логарифма
Стационарное решение
Решение приведенного выше дифференциального уравнения ( 9 ) в бесконечности времени (устойчивое состояние) имеет вид:
| 10а |
Приведенное выше уравнение ( 10а ) можно переписать как:
| 10б |
Вышеуказанное уравнение ( 10b ) проясняет связь между удалением массы и клиренсом . Оно утверждает, что (при постоянном образовании массы) концентрация и клиренс изменяются обратно пропорционально друг другу. Если применить это уравнение к креатинину (т. е. клиренсу креатинина ), то из уравнения следует, что если сывороточный креатинин удваивается, клиренс уменьшается вдвое, а если сывороточный креатинин учетверяется, клиренс уменьшается вчетверо.
Измерение почечного клиренса
Почечный клиренс можно измерить путем сбора мочи в определенное время и анализа ее состава с помощью следующего уравнения (которое непосредственно следует из вывода ( 10b )):
| 11 |
Где:
- K — клиренс [мл/мин]
- C U — концентрация мочи [ммоль/л] (в США часто [мг/мл])
- Q — поток мочи (объем/время) [мл/мин] (часто [мл/24 ч])
- C B — концентрация в плазме [ммоль/л] (в США часто [мг/мл])
Когда субстанция «С» — креатинин, эндогенное химическое вещество, которое выводится только путем фильтрации, клиренс является приближенным значением скорости клубочковой фильтрации . Клиренс инулина реже используется для точного определения скорости клубочковой фильтрации.
Примечание - приведенное выше уравнение ( 11 ) справедливо только для стационарного состояния. Если очищаемое вещество не находится в постоянной концентрации в плазме (т.е. не в стационарном состоянии), K должно быть получено из (полного) решения дифференциального уравнения ( 9 ).
Смотрите также
Ссылки
- ^ Ma, Guangda (2020). "Нелинейное устранение" (PDF) . clinpharmacol.fmhs.auckland.ac.nz . Получено 18 сентября 2023 г. .
- ^ ab Rowland M, Tozer TM (2011). Клиническая фармакокинетика и фармакодинамика, концепции и применение (4-е изд.). Baltimore MD: Lippincott Williams & Wilkins.
- ^ "Цели фармакокинетики". Pharmacology2000.com. 2006-12-27 . Получено 2013-05-06 .
- ^ Каплан Step1 Фармакология 2010, стр. 14
- ^ Райт, Сэмсон (1972). Прикладная физиология Сэмсона Райта. Сирил Артур Кил, Нил Эрик (12-е изд.). Лондон: English Language Book Society и Oxford University Press. ISBN 0-19-263321-X. OCLC 396722036.
- ^ Seldin DW (2004). «Развитие концепции очистки». Журнал нефрологии . 17 (1): 166–71 . PMID 15151274.
- ^ Бабб АЛ, Попович РП, Кристофер TG, Скрибнер БХ (1971). «Генезис гипотезы квадратного метра-часа». Труды Американского общества искусственных внутренних органов . 17 : 81–91 . PMID 5158139.
- ^ Риттер Дж., Флауэр Р., Хендерсон Г., Ранг Х. Фармакология Ранга и Дейла. 8-е изд. Лондон. Черчилль Ливингстон; 2015
- ^ abc Winter ME (2003). "Связывание плазматических белков". Базовая клиническая фармакокинетика (4-е изд.). Lippincott Williams & Wilkins. стр. 32. ISBN 978-0-7817-4147-7.
- ^ Gotch FA (1998). «Текущее место моделирования кинетики мочевины в отношении различных методов диализа». Нефрология, диализ, трансплантация . 13 (Suppl 6): 10– 4. doi : 10.1093/ndt/13.suppl_6.10 . PMID 9719197.Полный текст
- ^ Gotch FA, Sargent JA, Keen ML (август 2000 г.). «Whither gost Kt/V?». Kidney International . 76 (Suppl 76): S3-18. doi : 10.1046/j.1523-1755.2000.07602.x . PMID 10936795.





























