Хорда (воздухоплавание)

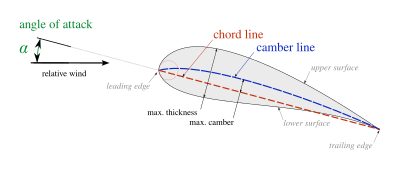
В аэронавтике хорда — это воображаемый отрезок прямой линии , соединяющий переднюю и заднюю кромки поперечного сечения аэродинамического профиля параллельно направлению воздушного потока. Длина хорды — это расстояние между задней и передней кромками. ^{[1] [2]} Точка на передней кромке, используемая для определения главной хорды, может быть точкой поверхности минимального радиуса. ^[2] Для аэродинамического профиля турбины хорда может быть определена линией между точками, где передняя и задняя части двумерного сечения лопасти касались бы плоской поверхности, если бы она была положена выпуклой стороной вверх. ^[3]

Крыло , горизонтальный стабилизатор , вертикальный стабилизатор и лопасти винта /ротора самолета все основаны на аэродинамических сечениях, и термин хорда или длина хорды также используется для описания их ширины. Хорда крыла, стабилизатора и винта определяется путем измерения расстояния между передней и задней кромками в направлении воздушного потока. (Если крыло имеет прямоугольную форму в плане , а не коническую или стреловидную, то хорда — это просто ширина крыла, измеренная в направлении воздушного потока.) Термин хорда также применяется к ширине закрылков , элеронов и руля направления на самолете.

Многие крылья не прямоугольные, поэтому они имеют разные хорды в разных положениях. Обычно длина хорды наибольшая там, где крыло соединяется с фюзеляжем самолета (так называемая корневая хорда ) и уменьшается вдоль крыла к кончику крыла ( концевая хорда ). Большинство реактивных самолетов используют конструкцию конического стреловидного крыла . Чтобы обеспечить характерную фигуру, которую можно сравнивать между различными формами крыла, используется средняя аэродинамическая хорда (сокращенно MAC ), хотя ее сложно вычислить. Средняя аэродинамическая хорда используется для расчета моментов тангажа. ^[4]

Хорда может быть также определена для компрессорных и турбинных аэродинамических поверхностей в газотурбинных двигателях, таких как турбореактивные , турбовинтовые или турбовентиляторные двигатели для воздушных судов.

Стандартная средняя хорда (СХ) определяется как площадь крыла, деленная на размах крыла: ^[5]

${\displaystyle {\mbox{SMC}}={\frac {S}{b}},}$

где S — площадь крыла, b — размах крыла. Таким образом, SMC — это хорда прямоугольного крыла с той же площадью и размахом, что и у данного крыла. Это чисто геометрическая фигура, и в аэродинамике она используется редко .

Средняя аэродинамическая хорда (САХ) определяется как: ^[6]

${\displaystyle {\mbox{MAC}}={\frac {2}{S}}}$${\displaystyle \int _{0}^{\frac {b}{2}}c(y)^{2}dy,}$

где y — координата вдоль размаха крыла, а c — хорда в координате y . Остальные термины такие же, как для SMC.

MAC — это двумерное представление всего крыла. Распределение давления по всему крылу можно свести к одной подъемной силе и моменту вокруг аэродинамического центра MAC. Поэтому часто важна не только длина, но и положение MAC. В частности, положение центра тяжести (ЦТ) самолета обычно измеряется относительно MAC, как процент расстояния от передней кромки MAC до ЦТ относительно самого MAC.

Обратите внимание, что рисунок справа подразумевает, что MAC возникает в точке, где изменяется размах передней или задней кромки. Это просто совпадение. В общем случае это не так. Любая форма, отличная от простой трапеции, требует оценки вышеуказанного интеграла.

Отношение длины (или размаха ) крыла прямоугольной формы в плане к его хорде известно как удлинение , важный показатель сопротивления , создаваемого крылом. ^[7] (Для крыльев с формой в плане, которая не является прямоугольной, удлинение рассчитывается как квадрат размаха, деленный на площадь крыла в плане.) Крылья с большим удлинением будут иметь меньшее индуктивное сопротивление, чем крылья с меньшим удлинением. Индуктивное сопротивление наиболее существенно на низких скоростях полета. Вот почему у планеров длинные тонкие крылья.

Зная площадь (S _w ), коэффициент конусности ( ) и размах (b) крыла, хорду в любой точке размаха можно рассчитать по формуле: ^[8]${\displaystyle \лямбда}$

${\displaystyle c(y)={\frac {2\,S_{w}}{(1+\lambda )b}}\left[1-{\frac {1-\lambda }{b}}|2y|\right].}$

где

${\displaystyle \lambda ={\frac {C_{\rm {Наконечник}}}{C_{\rm {Корень}}}}}$

• Аэродинамика для студентов
  • машина обратного пути:[1]
• Нахождение средней аэродинамической хорды (САХ)
• Калькулятор средней аэродинамической хорды (MAC) на основе изображения