Алгоритм генерации лабиринта

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Неиспользуемые материалы могут быть оспорены и удалены. Найти источники:  «Алгоритм генерации лабиринта» – новости  · газеты  · книги  · ученый  · JSTOR ( март 2018 г. ) ( Узнайте, как и когда удалять это сообщение )

Алгоритмы генерации лабиринтов — это автоматизированные методы создания лабиринтов .

Лабиринт можно сгенерировать, начав с предопределенного расположения ячеек (чаще всего это прямоугольная сетка, но возможны и другие варианты) с участками стен между ними. Это предопределенное расположение можно рассматривать как связный граф с ребрами, представляющими возможные участки стен, и узлами, представляющими ячейки. Целью алгоритма генерации лабиринта тогда можно считать создание подграфа, в котором сложно найти маршрут между двумя конкретными узлами.

Если подграф не связан , то есть области графа, которые пропадают, поскольку они не вносят вклад в пространство поиска. Если граф содержит петли, то между выбранными узлами может быть несколько путей. Из-за этого генерация лабиринта часто рассматривается как генерация случайного остовного дерева . Циклы, которые могут сбить с толку наивных решателей лабиринтов, могут быть введены путем добавления случайных ребер к результату в ходе работы алгоритма.

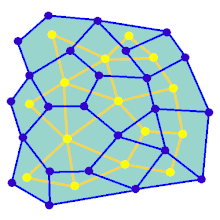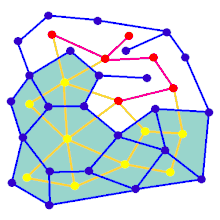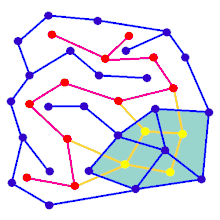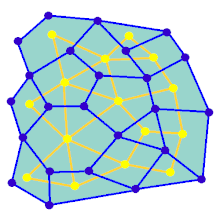
Анимация показывает шаги генерации лабиринта для графа, который не находится на прямоугольной сетке. Сначала компьютер создает случайный планарный граф G, показанный синим цветом, и его дуальный граф F, показанный желтым цветом. Затем компьютер проходит по F, используя выбранный алгоритм, например, поиск в глубину, окрашивая путь в красный цвет. Во время прохождения, когда красное ребро пересекает синее ребро, синее ребро удаляется. Наконец, когда все вершины F посещены, F стирается, а два ребра из G, одно для входа и одно для выхода, удаляются.

Этот алгоритм, также известный как алгоритм «рекурсивного обратного отслеживания», представляет собой рандомизированную версию алгоритма поиска в глубину .

Часто реализуемый с помощью стека , этот подход является одним из самых простых способов создания лабиринта с помощью компьютера. Рассмотрим пространство для лабиринта как большую сетку ячеек (как большая шахматная доска), каждая ячейка начинается с четырех стен. Начиная со случайной ячейки, компьютер затем выбирает случайную соседнюю ячейку, которая еще не была посещена. Компьютер удаляет стену между двумя ячейками и отмечает новую ячейку как посещенную, и добавляет ее в стек для облегчения возврата. Компьютер продолжает этот процесс, причем ячейка, у которой нет непосещенных соседей, считается тупиком. Когда он оказывается в тупике, он возвращается по пути, пока не достигнет ячейки с непосещенным соседом, продолжая генерацию пути, посещая эту новую непосещенную ячейку (создавая новое соединение). Этот процесс продолжается до тех пор, пока не будут посещены все ячейки, заставляя компьютер возвращаться к начальной ячейке. Мы можем быть уверены, что каждая ячейка посещена.

Как указано выше, этот алгоритм включает в себя глубокую рекурсию, которая может вызвать проблемы переполнения стека на некоторых компьютерных архитектурах. Алгоритм можно перестроить в цикл, сохранив информацию о возврате в самом лабиринте. Это также обеспечивает быстрый способ отображения решения, начиная с любой заданной точки и возвращаясь к началу.

Лабиринты, созданные с помощью поиска в глубину, имеют низкий коэффициент ветвления и содержат много длинных коридоров, поскольку алгоритм исследует как можно большую часть каждой ветви, прежде чем вернуться назад.

Алгоритм поиска в глубину генерации лабиринта часто реализуется с использованием возврата . Это можно описать следующей рекурсивной процедурой:

1. Если в качестве параметра указана текущая ячейка
2. Отметить текущую ячейку как посещенную
3. Пока у текущей ячейки есть непосещенные соседние ячейки
   1. Выберите одного из непосещенных соседей
   2. Удалить стену между текущей ячейкой и выбранной ячейкой
   3. Рекурсивно вызвать процедуру для выбранной ячейки

который вызывается один раз для любой начальной ячейки в области.

Недостатком первого подхода является большая глубина рекурсии — в худшем случае процедура может потребоваться повторить для каждой ячейки обрабатываемой области, что может превысить максимальную глубину стека рекурсии во многих средах. В качестве решения тот же метод обратного отслеживания может быть реализован с явным стеком , которому обычно разрешено расти намного больше без вреда.

1. Выберите начальную ячейку, отметьте ее как посещенную и поместите в стек.
2. Пока стек не пуст
   1. Извлечь ячейку из стека и сделать ее текущей ячейкой.
   2. Если у текущей ячейки есть соседи, которые не были посещены
      1. Поместить текущую ячейку в стек
      2. Выберите одного из непосещенных соседей
      3. Удалить стену между текущей ячейкой и выбранной ячейкой
      4. Отметить выбранную ячейку как посещенную и поместить ее в стек

Этот алгоритм представляет собой рандомизированную версию алгоритма Крускала .

1. Создайте список всех стен и создайте набор для каждой ячейки, каждый из которых будет содержать только эту одну ячейку.
2. Для каждой стены в случайном порядке:
   1. Если ячейки, разделенные этой стенкой, принадлежат разным множествам:
      1. Удалить текущую стену.
      2. Объедините множества ранее разделенных ячеек.

Существует несколько структур данных, которые можно использовать для моделирования наборов ячеек. Эффективная реализация с использованием структуры данных непересекающихся наборов может выполнять каждое объединение и операцию поиска для двух наборов за почти постоянное амортизированное время (в частности, время; для любого правдоподобного значения ), поэтому время выполнения этого алгоритма по существу пропорционально количеству стен, доступных для лабиринта.${\displaystyle O(\альфа (V))}$${\displaystyle \альфа (x)<5}$${\displaystyle x}$

Не имеет значения, является ли список стен изначально случайным или стена выбирается случайным образом из неслучайного списка, любой из способов одинаково легко закодировать.

Поскольку эффект этого алгоритма заключается в создании минимального остовного дерева из графа с одинаково взвешенными ребрами, он имеет тенденцию создавать регулярные шаблоны, которые довольно легко решить.

Этот алгоритм представляет собой рандомизированную версию алгоритма Прима .

1. Начните с сетки, состоящей из стен.
2. Выберите ячейку, отметьте ее как часть лабиринта. Добавьте стены ячейки в список стен.
3. Хотя в списке есть стены:
   1. Выберите случайную стену из списка. Если посещается только одна из ячеек, которые разделяет стена, то:
      1. Сделайте стену проходом и отметьте непосещенную ячейку как часть лабиринта.
      2. Добавьте соседние стены ячейки в список стен.
   2. Удалить стену из списка.

Обратите внимание, что простое выполнение классических Prim на графе со случайными весами ребер создаст лабиринты, стилистически идентичные лабиринтам Краскала, поскольку они оба являются алгоритмами минимального остовного дерева. Вместо этого этот алгоритм вводит стилистические вариации, поскольку ребра, расположенные ближе к начальной точке, имеют меньший эффективный вес.

Хотя классический алгоритм Прима хранит список ребер, для генерации лабиринта мы могли бы вместо этого хранить список смежных ячеек. Если случайно выбранная ячейка имеет несколько ребер, которые соединяют ее с существующим лабиринтом, выберите одно из этих ребер наугад. Это будет иметь тенденцию к немного большему ветвлению, чем версия на основе ребер выше.

Алгоритм можно упростить еще больше, если случайным образом выбирать ячейки, соседствующие с уже посещенными ячейками, вместо того чтобы отслеживать веса всех ячеек или ребер.

Обычно довольно легко найти путь к стартовой ячейке, но трудно найти путь куда-либо еще.

Все вышеперечисленные алгоритмы имеют смещения разного рода: поиск в глубину смещен в сторону длинных коридоров, в то время как алгоритмы Краскала/Прима смещены в сторону множества коротких тупиков. С другой стороны , алгоритм Уилсона ^{[1] генерирует} несмещенную выборку из равномерного распределения по всем лабиринтам, используя случайные блуждания со стертыми петлями .

Мы начинаем алгоритм с инициализации лабиринта с одной произвольно выбранной ячейкой. Затем мы начинаем с новой произвольно выбранной ячейки и выполняем случайное блуждание, пока не достигнем ячейки, уже находящейся в лабиринте, однако, если в какой-либо момент случайное блуждание достигает своего собственного пути, образуя петлю, мы стираем петлю с пути, прежде чем продолжить. Когда путь достигает лабиринта, мы добавляем его в лабиринт. Затем мы выполняем еще одно случайное блуждание со стертым циклом из другой произвольно выбранной начальной ячейки, повторяя это до тех пор, пока все ячейки не будут заполнены.

Эта процедура остается беспристрастной, независимо от того, какой метод мы используем для произвольного выбора начальных ячеек. Поэтому мы всегда можем выбрать первую незаполненную ячейку в (скажем) порядке слева направо, сверху вниз для простоты.

Алгоритм Олдоса-Бродера также создает однородные остовные деревья. Однако это один из наименее эффективных алгоритмов лабиринта. ^[2]

1. Выберите случайную ячейку в качестве текущей и отметьте ее как посещенную.
2. Пока есть непосещаемые ячейки:
   1. Выберите случайного соседа.
   2. Если выбранный сосед не был посещен:
      1. Удалить стену между текущей ячейкой и выбранным соседом.
      2. Отметьте выбранного соседа как посещенного.
   3. Сделать выбранную соседнюю ячейку текущей.

Иллюстрация рекурсивного деления

оригинальная камера	разделение двумя стенами	дыры в стенах	продолжить деление...	завершенный

Лабиринты можно создавать с помощью рекурсивного деления , алгоритма, который работает следующим образом: начните с пространства лабиринта без стен. Назовите это камерой. Разделите камеру случайно расположенной стеной (или несколькими стенами), где каждая стена содержит случайно расположенное отверстие для прохода внутри нее. Затем рекурсивно повторите процесс для подкамер, пока все камеры не станут минимального размера. Этот метод приводит к лабиринтам с длинными прямыми стенами, пересекающими их пространство, что упрощает определение того, какие области следует избегать.

Например, в прямоугольном лабиринте постройте в случайных точках две перпендикулярные друг другу стены. Эти две стены разделяют большую камеру на четыре меньшие камеры, разделенные четырьмя стенами. Выберите три из четырех стен наугад и откройте отверстие шириной в одну клетку в случайной точке каждой из трех. Продолжайте таким образом рекурсивно, пока каждая камера не будет иметь ширину в одну клетку в любом из двух направлений.

Это простой и быстрый способ создания лабиринта. ^[3]

На каждой итерации этот алгоритм создает лабиринт в два раза большего размера, копируя себя 3 раза. В конце каждой итерации открываются 3 пути между 4 меньшими лабиринтами.

Преимущество этого метода в том, что он очень быстрый. Недостаток в том, что невозможно получить лабиринт выбранного размера, но можно использовать различные трюки, чтобы обойти эту проблему.

Существуют другие алгоритмы, которым требуется только достаточно памяти для хранения одной линии 2D-лабиринта или одной плоскости 3D-лабиринта. Алгоритм Эллера предотвращает образование петель, сохраняя, какие ячейки в текущей строке соединены через ячейки в предыдущих строках, и никогда не удаляет стены между любыми двумя уже соединенными ячейками. ^[4] Алгоритм Sidewinder начинается с открытого прохода вдоль всего верхнего ряда, а последующие ряды состоят из более коротких горизонтальных проходов с одним соединением с проходом выше. Алгоритм Sidewinder тривиально решать снизу вверх, поскольку у него нет восходящих тупиков. ^[5] При заданной начальной ширине оба алгоритма создают идеальные лабиринты неограниченной высоты.

Большинство алгоритмов генерации лабиринтов требуют поддержания отношений между ячейками внутри него, чтобы гарантировать, что результат будет разрешимым. Однако допустимые односвязные лабиринты можно сгенерировать, сосредоточившись на каждой ячейке независимо. Двоичный древовидный лабиринт — это стандартный ортогональный лабиринт, в котором каждая ячейка всегда имеет проход, ведущий вверх или влево, но никогда оба. Чтобы создать двоичный древовидный лабиринт, для каждой ячейки подбросьте монетку, чтобы решить, добавлять ли проход, ведущий вверх или влево. Всегда выбирайте одно и то же направление для ячеек на границе, и результатом будет допустимый односвязный лабиринт, который выглядит как двоичное дерево , с верхним левым углом — его корнем. Как и в случае с Sidewinder, двоичный древовидный лабиринт не имеет тупиков в направлениях смещения.

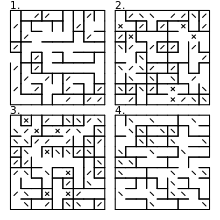
Схожая форма подбрасывания монеты для каждой ячейки — создание изображения с использованием случайной смеси символов прямого и обратного слеша. Это не создает действительный односвязный лабиринт, а скорее выборку замкнутых контуров и уникурсальных проходов. В руководстве для Commodore 64 представлена ​​программа BASIC, использующая этот алгоритм, с использованием вместо этого графических символов диагональной линии PETSCII для более плавного графического вида.

Некоторые типы клеточных автоматов могут быть использованы для создания лабиринтов. ^[6] Два известных таких клеточных автомата, Maze и Mazectric, имеют строки правил B3/S12345 и B3/S1234. ^[6] В первом случае это означает, что клетки выживают из одного поколения в другое, если у них есть по крайней мере один и не более пяти соседей . Во втором случае это означает, что клетки выживают, если у них есть от одного до четырех соседей. Если у клетки ровно три соседа, она рождается. Это похоже на игру Конвея «Жизнь» в том, что шаблоны, в которых нет живой клетки, соседствующей с 1, 4 или 5 другими живыми клетками в любом поколении, будут вести себя идентично ей. ^[6] Однако для больших шаблонов это ведет себя совсем не так, как у Жизни. ^[6]

Для случайного начального шаблона эти клеточные автоматы, генерирующие лабиринты, будут развиваться в сложные лабиринты с четко определенными стенами, очерчивающими коридоры. Mazecetric, имеющий правило B3/S1234, имеет тенденцию генерировать более длинные и прямые коридоры по сравнению с Maze, с правилом B3/S12345. ^[6] Поскольку эти правила клеточных автоматов являются детерминированными , каждый сгенерированный лабиринт однозначно определяется его случайным начальным шаблоном. Это существенный недостаток, поскольку лабиринты, как правило, относительно предсказуемы.

Как и некоторые из описанных выше методов, основанных на теории графов, эти клеточные автоматы обычно генерируют лабиринты из единственного начального шаблона; следовательно, обычно будет относительно легко найти путь к начальной ячейке, но сложнее найти путь в любую другую ячейку.

• Алгоритм решения лабиринта
• Самоизбегающая прогулка
• Поиск методом перебора

• Think Labyrinth: алгоритмы лабиринтов (подробности об этих и других алгоритмах генерации лабиринтов)
• Джеймис Бак: презентация HTML 5 с демонстрациями алгоритмов генерации лабиринтов
• Визуализация генерации лабиринта
• Реализация алгоритма Прима на языке Java
• Реализации алгоритма создания лабиринта DFS на нескольких языках в Rosetta Code
• Армин Райхерт: 34 алгоритма лабиринта на Java 8 с демонстрационным приложением
• Задача по кодированию № 10.1: Генератор лабиринтов с p5.js — Часть 1: Алгоритм генерации лабиринтов в JavaScript с p5
• Генератор лабиринтов Чарльза Бонда, журнал COMPUTE!, декабрь 1981 г.