Математическое обсуждение дальномерности

В военно-морской артиллерии , когда стали доступны дальнобойные орудия, вражеский корабль перемещался на некоторое расстояние после выстрела снарядов. Возникла необходимость выяснить, где будет находиться вражеский корабль, цель, когда прилетят снаряды. Процесс отслеживания вероятного местонахождения корабля назывался измерением дальности, потому что расстояние до цели — дальность — было очень важным фактором для точного наведения орудий. Со временем поезд (также называемый пеленгом), направление на цель, также стал частью измерения дальности, но традиция сохранила этот термин.

Дальномерное наблюдение — прекрасный пример применения аналоговых вычислений к реальной задаче математического моделирования. Поскольку страны вложили так много денег в свои крупные корабли , они были готовы вложить огромные суммы денег в разработку оборудования для дальномерного наблюдения , чтобы гарантировать, что орудия этих кораблей смогут направлять свои снаряды в цель. В этой статье представлен обзор дальномерного наблюдения как задачи математического моделирования. Чтобы сделать это обсуждение более конкретным, в качестве фокуса этого обсуждения используется Ford Mk 1 Rangekeeper. Ford Mk 1 Rangekeeper был впервые развернут на USS Texas  в 1916 году во время Первой мировой войны . Это относительно хорошо документированный дальномер, который имел длительный срок службы. [1] Хотя это и ранняя форма механического дальномерного наблюдения, он иллюстрирует все основные принципы. [2] Дальномерные наблюдения других стран использовали похожие алгоритмы для вычисления углов орудия, но часто существенно отличались в своем оперативном использовании. [3]

В дополнение к дальнобойной стрельбе, запуск торпед также требует функции, похожей на поддержание дальности. [4] Военно-морской флот США во время Второй мировой войны имел TDC , которая была единственной системой управления торпедным огнем подводных лодок эпохи Второй мировой войны, включавшей механический поддержание дальности (другие флоты полагались на ручные методы). Также существовали устройства поддержания дальности для использования с торпедами, запускаемыми с надводных кораблей. Для обзора поддержания дальности за пределами ВМС США, есть подробная ссылка, в которой обсуждается математика поддержания дальности, связанная с управлением торпедным огнем в Императорском флоте Японии . [5]

Нижеследующее обсуждение построено по образцу презентаций, содержащихся в руководствах по артиллерийскому делу ВМС США времен Второй мировой войны. [6]

Анализ

Система координат

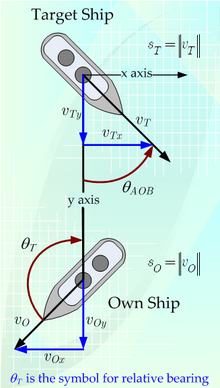
Рисунок 1: Система координат Rangekeeper. Система координат имеет цель в качестве начала отсчета. Диапазон значений оси Y до цели.

Дальномерщики ВМС США во время Второй мировой войны использовали подвижную систему координат, основанную на линии визирования (LOS) между кораблем, стреляющим из своего орудия (известным как «собственный корабль»), и целью (известной как «цель»). Как показано на рисунке 1, дальномер определяет «ось y» как LOS, а «ось x» как перпендикуляр к LOS с началом двух осей, центрированным на цели.

Важным аспектом выбора системы координат является понимание знаков различных скоростей. Скорость изменения пеленга положительна в направлении по часовой стрелке. Скорость изменения дальности положительна для увеличения дальности цели.

Отслеживание цели

Общий подход

Во время Второй мировой войны отслеживание цели означало постоянное знание дальности и пеленга цели. Эти параметры цели периодически фиксировались моряками, обслуживающими артиллерийские установки [7] и радарные системы, которые затем передавали данные дальномеру. Дальномер выполнял линейную экстраполяцию дальности и пеленга цели как функции времени на основе выборок информации о цели.

В дополнение к наблюдениям за целями с борта корабля, дальномерщики могли также получать данные с корректирующих самолетов или даже пилотируемых аэростатов, привязанных к собственному кораблю. Эти платформы для обнаружения целей можно было запускать и поднимать с больших военных кораблей, таких как линкоры. В целом, наблюдения за целями, проводимые корабельными приборами, были предпочтительны для целей на расстоянии менее 20 000 ярдов, а наблюдения с самолетов были предпочтительны для целей на большем расстоянии. [8] После Второй мировой войны стали доступны вертолеты, и необходимость проводить опасные операции по запуску и подъему корректирующих самолетов или аэростатов отпала (см. краткое обсуждение линкора класса «Айова» ).

Во время Первой мировой войны информация об отслеживании целей часто представлялась на листе бумаги. [9] Во время Второй мировой войны информация об отслеживании могла отображаться на электронных дисплеях (см. авианосец класса «Эссекс» для обсуждения распространенных дисплеев).

Диапазон цели

В начале Второй мировой войны дальность до цели измерялась оптическими дальномерами . Хотя некоторые ночные операции проводились с использованием прожекторов и звездных снарядов, в целом оптические дальномеры были ограничены дневной работой. [10] Во второй половине Второй мировой войны для определения дальности до цели использовался радар. Радар оказался точнее [11] , чем оптические дальномеры (по крайней мере, в условиях эксплуатации) [12] и был предпочтительным способом определения дальности до цели как ночью, так и днем. [13]

Скорость цели

В начале Второй мировой войны измерения дальности и пеленга цели производились в течение определенного периода времени и вручную наносились на карту. [14] Скорость и курс цели можно было вычислить, используя расстояние, пройденное целью за определенный промежуток времени. Во второй половине Второй мировой войны скорость цели можно было измерить с помощью данных радара. Радар обеспечивал точную скорость пеленга, дальность и радиальную скорость, которые затем преобразовывались в курс и скорость цели.

В некоторых случаях, например, с подводными лодками, скорость цели можно оценить с помощью данных гидролокатора. Например, оператор гидролокатора может измерить скорость вращения винта акустически и, зная класс судна , вычислить скорость судна (см. TDC для получения дополнительной информации).

Целевой курс

Рисунок 2: Определение угла на носу. На этой иллюстрации показано, как Императорский флот Японии использовал измерение угла, образуемого кораблем, для оценки угла корабля на носу.

Курс цели был наиболее сложной частью данных цели для получения. Во многих случаях вместо измерения курса цели многие системы измеряли связанную величину, называемую углом на носу . Угол на носу — это угол, образованный курсом судна и линией визирования (см. Рисунок 1).

Угол на носу обычно оценивался на основе опыта наблюдений наблюдателя. В некоторых случаях наблюдатели улучшали свои способности оценки, практикуясь против моделей кораблей, установленных на « ленивой Сьюзан ». [15] Императорский флот Японии имел уникальный инструмент, называемый Сокутэкибан (測的盤), [16] , который использовался для помощи наблюдателям в измерении угла на носу. Наблюдатель сначала использовал это устройство для измерения угловой ширины цели. Зная угловую ширину цели, дальность до цели и известную длину этого класса корабля , угол на носу цели можно вычислить с помощью уравнений, показанных на рисунке 2.

Для определения угла на носу требовались человеческие наблюдатели. Чтобы сбить с толку людей-наблюдателей, корабли часто использовали ослепляющий камуфляж , который заключался в нанесении линий на корабль с целью затруднить определение угла цели на носу. Хотя ослепляющий камуфляж был полезен против некоторых типов оптических дальномеров, этот подход был бесполезен против радаров и вышел из моды во время Второй мировой войны.

Прогнозирование положения

Прогнозирование положения корабля-цели в момент попадания снаряда имеет решающее значение, поскольку это положение, на которое должны быть направлены орудия собственного корабля. Во время Второй мировой войны большинство дальномерщиков выполняли прогнозирование положения, используя линейную экстраполяцию курса и скорости цели. Хотя корабли маневренны, большие корабли маневрируют медленно, и линейная экстраполяция является разумным подходом во многих случаях. [17]

Во время Первой мировой войны дальномерщиков часто называли «часами» (например, см. часы дальности и пеленга в Таблице управления огнем Дрейера). Эти устройства назывались часами, потому что они регулярно увеличивали оценку дальности цели и угла, используя фиксированные значения. Такой подход имел ограниченное применение, поскольку изменения пеленга цели являются функцией дальности, а использование фиксированного изменения приводит к тому, что прогноз пеленга цели быстро становится неточным. [18]

Диапазон

Рисунок 3: Определение скорости изменения дальности дальномерщиком. На этой иллюстрации показано, как дальномер определяет скорость изменения дальности.

Дальность до цели в момент попадания снаряда можно оценить с помощью уравнения 1, которое показано на рисунке 3.

(Уравнение 1) Р Т П = Р Т + г Р Т г т ⋅ т Т О Ф ′ = Р Т + г Р Т г т ⋅ ( т Т О Ф + т Д е л а у ) {\displaystyle {\begin{array}{lcr}R_{TP}&=&R_{T}+{\frac {dR_{T}}{dt}}\cdot t_{TOF'}\\&=&R_{T}+{\frac {dR_{T}}{dt}}\cdot \left(t_{TOF}+t_{Delay}\right)\end{array}}}

где

  • Р Т П {\displaystyle R_{TP}\,} дальность до цели в момент попадания снаряда.
  • Р Т {\displaystyle R_{T}\,} дальность до цели в момент выстрела.
  • т Т О Ф ′ {\displaystyle t_{TOF'}\,} это время полета снаряда плюс задержки срабатывания системы [19] , т.е. . ( т Т О Ф ) {\displaystyle \left(t_{TOF}\right)\,}
    ( т Д е л а у ) {\displaystyle \left(t_{Delay}\right)\,} т Т О Ф ′ = т Т О Ф + т Д е л а у {\displaystyle t_{TOF'}=t_{TOF}+t_{Delay}\,}

Точное предсказание дальности цели в момент попадания снаряда затруднено, поскольку для этого требуется знать время полета снаряда, которое является функцией прогнозируемого положения цели. Хотя этот расчет можно выполнить методом проб и ошибок, это не было практичным подходом с аналоговым компьютерным оборудованием, доступным во время Второй мировой войны. В случае Ford Rangekeeper Mk 1 время полета было приблизительно рассчитано путем предположения, что время полета линейно пропорционально дальности, как показано в уравнении 2. [20]

(Уравнение 2) Р Т П = Р Т + г Р Т г т ⋅ ( к Т О Ф ⋅ Р Т + т Д е л а у ) {\displaystyle R_{TP}=R_{T}+{\frac {dR_{T}}{dt}}\cdot \left(k_{TOF}\cdot R_{T}+t_{Delay}\right)\,\!}

где

  • к Т О Ф {\displaystyle k_{TOF}\,} — константа пропорциональности между временем пролета (TOF) и дальностью до цели.

Предположение о том, что TOF линейно пропорционален диапазону, является грубым и может быть улучшено за счет использования более сложных средств оценки функций.

Прогнозирование диапазона требует знания скорости изменения диапазона. Как показано на рисунке 3, скорость изменения диапазона может быть выражена, как показано в уравнении 3.

(Уравнение 3) г Р Т г т = − с О у − с Т у {\displaystyle {\frac {dR_{T}}{dt}}=-s_{Oy}-s_{Ty}\,\!}

где

  • с О у {\displaystyle s_{Oy}\,} — скорость собственного судна вдоль линии прицеливания, где . в О у = ‖ в О ‖ ⋅ потому что ⁡ ( θ Т ) {\displaystyle v_{Oy}=\lVert v_{O}\rVert \cdot \cos(\theta _{T})}
  • с Т у {\displaystyle s_{Тай}\,} — целевая скорость корабля вдоль линии прицеливания, где . в Т у = ‖ в Т ‖ ⋅ потому что ⁡ ( θ А О Б ) {\displaystyle v_{Ty}=\lVert v_{T}\rVert \cdot \cos(\theta _{AOB})}

Уравнение 4 показывает полное уравнение для прогнозируемого диапазона.

(Уравнение 4) Р Т П = Р Т + ( − с О у − с Т у ) ⋅ ( к Т О Ф ⋅ Р Т + т Д е л а у ) {\displaystyle R_{TP}=R_{T}+\left(-s_{Oy}-s_{Ty}\right)\cdot \left(k_{TOF}\cdot R_{T}+t_{Delay}\right)\,\!}

Азимут

Рисунок 4: Определение угловой скорости дальномерщиком. Расчет угловой скорости требует знания курса цели и собственного судна, скорости и дальности.

Прогнозирование азимута [21] выполняется аналогично прогнозированию дальности. [1] Уравнение 5 является фундаментальным соотношением, вывод которого проиллюстрирован на рисунке 4.

(Уравнение 5) θ Т П = θ Т + г θ Т г т ⋅ т Т О Ф ′ = θ Т + г θ Т г т ⋅ ( т Т О Ф + т Д е л а у ) {\displaystyle {\begin{array}{lcr}\theta _{TP}&=&\theta _{T}+{\frac {d\theta _{T}}{dt}}\cdot t_{TOF'}\\&=&\theta _{T}+{\frac {d\theta _{T}}{dt}}\cdot \left(t_{TOF}+t_{Delay}\right)\\\end{array}}}

где

  • θ Т {\displaystyle \theta _{T}\,} азимут на цель в момент выстрела из орудия.
  • θ Т П {\displaystyle \theta _{TP}\,} азимут на цель в момент попадания снаряда.

Скорость изменения подшипника можно рассчитать с помощью уравнения 6, которое показано на рисунке 4.

(Уравнение 6) г θ Т г т = с Т х + с О х Р Т {\displaystyle {\frac {d\theta _{T}}{dt}}={\frac {s_{Tx}+s_{Ox}}{R_{T}}}\,\!}

где

  • с О х {\displaystyle s_{Ox}\,} — собственная скорость судна по оси x, т.е. . с О х = ‖ в О ‖ ⋅ грех ⁡ ( θ Т ) {\displaystyle s_{Ox}=\lVert v_{O}\rVert \cdot \sin(\theta _{T})\,}
  • с Т х {\displaystyle s_{Tx}\,} — целевая скорость вдоль оси x, т.е. . с Т х = ‖ в Т ‖ ⋅ грех ⁡ ( θ А О Б ) {\displaystyle s_{Tx}=\lVert v_{T}\rVert \cdot \sin(\theta _{AOB})\,}

Подставив , уравнение 7 показывает окончательную формулу для прогнозируемого пеленга. т Т О Ф = ˙ к Т О Ф ⋅ Р Т {\displaystyle t_{TOF}{\dot {=}}k_{TOF}\cdot R_{T}}

(Уравнение 7) θ Т П = θ Т + ( с Т х + с О х Р Т ) ⋅ ( к Т О Ф ⋅ Р Т + т Д е л а у ) {\displaystyle \theta _{TP}=\theta _{T}+\left({\frac {s_{Tx}+s_{Ox}}{R_{T}}}\right)\cdot \left(k_{TOF}\cdot R_{T}+t_{Delay}\right)}

Баллистическая коррекция

Рисунок 5: Иллюстрация функции, основанной на кулачках Во время Второй мировой войны кулачки подвергались точной обработке для представления таблиц стрельбы для дальнобойной артиллерии.

Артиллерийская стрельба по целям за пределами прямой видимости исторически требовала расчетов на основе таблиц стрельбы. [22] Точка попадания снаряда является функцией многих переменных: [23]

  • Температура воздуха
  • Плотность воздуха
  • Ветер
  • Диапазон
  • вращение Земли
  • Характеристики снаряда, взрывателя, оружия
  • Начальная скорость пули
  • Температура топлива
  • Дрейф
  • Параллакс между орудиями и дальномерами и радиолокационными системами
  • Разница высот между целью и артиллерийским орудием

Таблицы стрельбы предоставляют данные для артиллерийского орудия, стреляющего в стандартизированных условиях, и поправки, необходимые для определения точки попадания в реальных условиях. [24] Было несколько способов реализовать таблицу стрельбы с использованием кулачков. Рассмотрим, например, рисунок 5. В этом случае угол наклона орудия как функция дальности цели и относительной высоты цели представлен толщиной кулачка на заданном осевом расстоянии и угле. Офицер наведения орудия вводил дальность цели и относительную высоту с помощью циферблатов. Затем высота штифта представляет собой требуемый угол наклона орудия. Эта высота штифта могла использоваться для привода кулачков или шестерен, которые вносили бы другие поправки, например, для температуры пороха и типа снаряда.

Кулачки, используемые в дальномерах, должны были быть очень точно обработаны, чтобы точно направлять пушки. Поскольку эти кулачки были обработаны по спецификациям, составленным из таблиц данных, они стали ранним применением станков с ЧПУ . [25]

В дополнение к целевым и баллистическим поправкам, дальномер также должен вносить поправки на волнообразное движение корабля. Военные корабли имели гироскоп с вертикальной осью вращения. Этот гироскоп определял два угла, которые определяли наклон палубы корабля относительно вертикали. Эти два угла передавались дальномеру, который применял поправку на основе этих углов. [26]

В то время как разработчики дальномерных прицелов тратили огромное количество времени на работу по минимизации источников ошибок в расчетах дальномерных прицелов, были ошибки и неопределенности информации, которые способствовали тому, что снаряды не попадали в цели при первом выстреле. [25] Дальномерные прицелы имели циферблаты, которые позволяли вручную вносить поправки в решение дальномерных прицелов. Когда артиллерийские корректировщики вызывали поправку, операторы дальномерных прицелов вручную вносили поправку с помощью этих циферблатов. [1]

Примечания

  1. ^ abc Mindell, David (2002). Между человеком и машиной . Балтимор: Университет Джонса Хопкинса. Приложение A. ISBN 0-8018-8057-2.
  2. ^ Улучшения в технологии дальномерного оружия для стрельбы на большие расстояния в основном касались автоматизированного управления пушкой и внедрения более совершенных датчиков, таких как радар. Основные уравнения управления огнем остались прежними.
  3. ↑ Брэдли Фишер (2003-09-09). "Обзор конструкции баллистических компьютеров для боевых кораблей ВМС США и Японии". NavWeaps . Получено 26-08-2006 .
  4. ^ Функции поддержания дальности торпеды и дальнобойного орудия различаются по масштабу. Например, время полета торпеды намного больше, чем у снаряда главного орудия линкора. Преимущества снаряда в скорости и скорострельности делают возможными выстрелы на дальность. Время полета торпеды настолько велико, что выстрелы на дальность невозможны. В некоторых работах эти вопросы рассматриваются.
  5. ^ Джексон, USNR, лейтенант (младший гвардеец) JG (февраль 1946 г.). Управление огнем японских торпед (PDF) . Техническая миссия ВМС США в Японию. Fascicle O-1, Target O-32. Архивировано из оригинала (PDF) 20 июля 2007 г.
  6. ^ "Глава 19: Проблема управления наземным огнем". Военно-морское вооружение и артиллерийское дело. Аннаполис, Массачусетс: Военно-морская академия США. 1958 [1950]. NavPers 10798-A . Получено 26.08.2006 .
  7. ^ "Глава 20: Директора артиллерии". Военно-морское вооружение и артиллерийское дело. Аннаполис, Массачусетс: Военно-морская академия США. 1958 [1950]. NavPers 10798-A . Получено 15 октября 2006 г.
  8. ^ Юренс, Уильям (2004-12-24). "Эволюция артиллерийского огня линкоров в ВМС США, 1920-1945". Navweaps.com. Архивировано из оригинала 2006-11-20 . Получено 18.10.2006 . Обычно ожидалось, что воздушное пятно будет иметь небольшой эффект на дистанциях менее 20 000 ярдов, где визуальное обнаружение оставалось превосходным. Преимущество воздушного пятна заметно возросло после этого. В 1935 году Военно-морской военный колледж подсчитал, что на расстоянии 29 000 ярдов воздушное пятно, как ожидается, даст в шесть раз больше попаданий, чем наблюдение от наблюдателей на высоте.
  9. ^ Построение графиков производилось либо вручную, либо с помощью механического плоттера в случае стола Дрейера.
  10. ^ Например, в статье « Битва у острова Саво» есть фотография, на которой изображен корабль, освещенный прожектором.
  11. ^ Норман, Фридман (1981). Военно-морской радар. Conway Maritime Press. ISBN 0-85177-238-2. Получено 20.10.2006 . Радар Mk 8: Точность дальности: 15 ярдов (5 м)
  12. ^ Лиенау, Питер; Тони ДиДжулиан (16.07.2001). "Немецкие оптические дальномеры". Navweps.com . Получено 20.10.2006 . Возьмем другой пример: американские линкоры классов North Carolina , South Dakota и Iowa имели главные директорные дальномеры 25-кратного увеличения с базовой длиной 26 футов 6 дюймов (8,0772 м)... Например, чтобы найти ошибку на 20 000 м, просто умножьте 0,97 м на 20 000 / 2 000 = 9,7 м.
  13. ^ Имеющиеся данные показывают, что уровни точности оптических дальномеров и радаров были сопоставимы при идеальных оптических условиях. Производительность оптического дальномера быстро ухудшалась под воздействием погодных условий, в то время как радар оставался нетронутым. Надежность радара была критическим фактором его популярности среди военно-морских сил.
  14. ^ "Глава 19C1". Военно-морская артиллерия и артиллерия: Том 2 Управление огнем. Бюро военно-морского персонала. 1958 [1950]. NavPers 10798-A.
  15. ^ О'Кейн, Ричард Х. (1989) [1987]. "Часть 4: Глава 1". Wahoo: Патрули самой известной американской подводной лодки Второй мировой войны (ред. Bantam). Нью-Йорк: Bantam. стр.  108–109 . ISBN  0-553-28161-5. Возможность и разделение ответственности были новыми для наших подводных сил. Я ответил просто: «Я ценю ваше доверие, капитан», и сказал ему, что отправляюсь в Сперри , чтобы сделать ленивую Сьюзан для наших моделей кораблей. Мне нужно, чтобы они отточили способность быстро и точно определять углы на носу... Через один ствол перевернутого бинокля 7x35 я определил углы из люка кладовой на реалистичной цели.
  16. ^ Брэдли Фишер (2003-09-09). "Обзор конструкции баллистического компьютера для боевых кораблей ВМС США и IJN". NavWeaps . Получено 2006-08-26 . Если известна длина цели и текущая дальность, оператор измеряет кажущуюся длину корабля в форме измерения пеленга (используя корму в качестве точки отсчета). Формула: угол инклинометра = L × Cos Ø / R, где: L — длина корабля, Ø — угол цели, а R — текущая дальность.
  17. ^ В некоторой степени точность этого приближения зависит от времени полета снаряда. На максимальной дальности 16-дюймовые орудия линкора класса Iowa имели время полета ~95 секунд. Корабли, вступающие в бой на таком расстоянии, были бы очень необычными. Самый продолжительный успешный бой между двумя военными кораблями произошел на расстоянии ~26 500 ярдов. Снаряд в этом случае имел бы время полета ~40 секунд (на основе 16-дюймовых орудий класса Iowa ).
  18. ^ "Dreyer Fire Control Table". Проект "Дредноут " . Получено 30 октября 2006 г. Азимутальный датчик в основном использовался в думареске и позволял устанавливать постоянную скорость азимута... Постоянный выходной сигнал скорости дальномерного датчика поступал в дифференциальное устройство, называемое корректором срабатывания, чья передача мультиплексировала его на три дополнительных пункта назначения.
  19. ^ Эта задержка — это интервал времени между заданным временем стрельбы и фактическим временем стрельбы. Этот временной интервал включает любые задержки из-за времени передачи данных на башню и механической активности, необходимой для стрельбы из оружия.
  20. ^ Минделл, Дэвид (2002). Между человеком и машиной . Балтимор: Университет Джонса Хопкинса. стр. 325. ISBN 0-8018-8057-2. Прибор Ford Rangekeeper рассматривает время полета как линейно пропорциональное расстоянию, что является лишь приближением.
  21. ^ Армия США использует азимут, а ВМС США — поезд. Это два слова для одного и того же понятия — горизонтального угла цели.
  22. ^ Таблица дальности стрельбы 16-дюймовых орудий 50 калибра. Бюро вооружений. 11.03.1944. Памфлет вооружений № 1091. Получено 29.10.2006 .
  23. ^ "Полевой устав армии США 6-40 Глава 7". Армия США. 2003-09-09 . Получено 2006-10-13 .
  24. ^ "Глава 17". Том 2 Управление огнем (редакция 1958 г.). Аннаполис, Массачусетс: Военно-морская академия США. 1958 [1950]. NavPers 10798-A . Получено 26.08.2006 .
  25. ^ ab A. Ben Clymer (1993). "Механические аналоговые компьютеры Ганнибала Форда и Уильяма Ньюэлла" (PDF) . IEEE Annals of the History of Computing . 15 (2) . Получено 26.08.2006 .
  26. ^ "Глава 19". Проблема управления огнем на поверхности (редакция 1958 г.). Аннаполис, Массачусетс: Военно-морская академия США. 1958 [1950]. NavPers 10798-A . Получено 26.08.2006 .
  • Отчет ВМС США о технологии торпедных аппаратов IJN: В отчете показано, что Императорский флот Японии использовал тот же подход, что и ВМС США, для функции поддержания дальности.
  • British Fire Control: Британское руководство по стрельбе, в котором обсуждается подход к управлению орудием дальнего действия.
  • Таблицы стрельбы: презентация PowerPoint по таблицам стрельбы
Retrieved from "https://en.wikipedia.org/w/index.php?title=Mathematical_discussion_of_rangekeeping&oldid=1270337249"