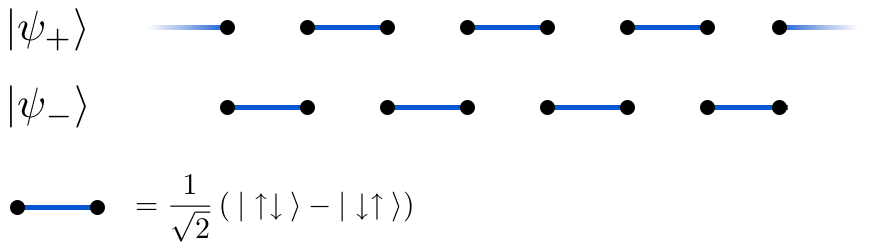Модель Маджумдара–Гхоша

Модель Маджумдара –Гоша — это одномерная квантовая спиновая модель Гейзенберга , в которой антиферромагнитное обменное взаимодействие ближайших соседей в два раза сильнее, чем взаимодействие следующих ближайших соседей. Это частный случай более общей модели — с . Модель названа в честь индийских физиков Чанчала Кумара Маджумдара и Дипана Гоша . ^[1]${\displaystyle J_{1}}$${\displaystyle J_{2}}$${\displaystyle J_{1}=2J_{2}}$

Модель Маджумдара–Гоша примечательна тем, что ее основные состояния (квантовые состояния с наименьшей энергией) можно точно найти и записать в простой форме, что делает ее полезной отправной точкой для понимания более сложных спиновых моделей и фаз.

Модель Маджумдара–Гоша определяется следующим гамильтонианом :

${\displaystyle {\hat {H}}=J\sum _{j=1}^{N}{\vec {S}}_{j}\cdot {\vec {S}}_{j+1} +{\frac {J}{2}}\sum _{j=1}^{N}{\vec {S}}_{j}\cdot {\vec {S}}_{j+2}}$

где вектор S представляет собой квантовый оператор спина с квантовым числом  S  = 1/2.

В литературе могут быть приняты и другие соглашения для коэффициентов, но наиболее важным фактом является то, что отношение связей первого соседа к связям второго соседа составляет 2 к 1. В результате этого отношения можно выразить гамильтониан (смещенный на общую константу) эквивалентно в форме

${\displaystyle {\hat {H}}={\frac {J}{4}}\sum _{j=1}^{N}({\vec {S}}_{j-1}+{\ век {S}}_{j}+{\vec {S}}_{j+1})^{2}}$

Суммарная величина есть не что иное, как квадратичный оператор Казимира для представления спиновой алгебры на трех последовательных сайтах , который в свою очередь может быть разложен в прямую сумму представлений спина 1/2 и 3/2. Он имеет собственные значения для подпространства спина 1/2 и для подпространства спина 3/2.${\displaystyle j-1,j,j+1}$${\displaystyle {\tfrac {1}{2}}({\tfrac {1}{2}}+1)={\tfrac {3}{4}}}$${\displaystyle {\tfrac {3}{2}}({\tfrac {3}{2}}+1)=15/4}$

Было показано, что модель Маджумдара–Гоша имеет два состояния минимальной энергии, или основных состояния, а именно состояния, в которых соседние пары спинов образуют синглетные конфигурации. Волновая функция для каждого основного состояния является произведением этих синглетных пар. Это объясняет, почему должно быть по крайней мере два основных состояния с одинаковой энергией, поскольку одно может быть получено из другого простым сдвигом или трансляцией системы на один шаг решетки. Более того, было показано, что эти (и их линейные комбинации) являются уникальными основными состояниями.

Модель Маджумдара–Гоша является одной из немногих реалистичных квантовых спиновых моделей, которые могут быть решены точно. Более того, ее основные состояния являются простыми примерами того, что известно как твердые тела с валентными связями (VBS). Таким образом, модель Маджумдара–Гоша связана с другой известной спиновой моделью, моделью AKLT , чье основное состояние является уникальным одномерным твердым телом с валентными связями со спином один (S=1).

Модель Маджумдара–Гоша также является полезным примером теоремы Либа–Шульца–Маттиса , которая грубо утверждает, что бесконечная одномерная полунечетно-целочисленная спиновая система должна либо не иметь энергетического зазора (или щели) между ее основным и возбужденным состояниями, либо иметь более одного основного состояния. Модель Маджумдара–Гоша имеет щель и попадает под второй случай.

Изотропность модели на самом деле не важна для того факта, что она имеет точно димеризованное основное состояние. Например, также имеет то же самое вышеупомянутое точно димеризованное основное состояние для всех реальных .${\displaystyle {\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{ Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z} _{j}{Z}_{j+2})}$${\displaystyle \дельта >-1/2}$

• Модель Гейзенберга (квантовая)
• Модель Гейзенберга (классическая)
• Модель J1 J2
• Бете-анзац
• модель Изинга
• модель тДж

• CK Majumdar и D Ghosh, О взаимодействии следующего ближайшего соседа в линейной цепи . J. Math. Phys. 10 , 1388 (1969); doi : 10.1063/1.1664978
• CK Majumdar, Антиферромагнитная модель с известным основным состоянием . J. Phys. C: Solid State Phys. 3 911–915 (1970)
• Асса Ауэрбах, Взаимодействующие электроны и квантовый магнетизм , Springer-Verlag New York (1992) стр. 83