М-теория
| Теория струн |
|---|
 |
| Фундаментальные объекты |
| Пертурбативная теория |
|
| Непертурбативные результаты |
| Феноменология |
| Математика |
M-теория — это теория в физике , которая объединяет все последовательные версии теории суперструн . Эдвард Виттен впервые предположил существование такой теории на конференции по теории струн в Университете Южной Калифорнии в 1995 году. Заявление Виттена инициировало шквал исследовательской деятельности, известный как вторая революция суперструн . До заявления Виттена теоретики струн определили пять версий теории суперструн. Хотя эти теории изначально казались очень разными, работа многих физиков показала, что теории связаны сложными и нетривиальными способами. Физики обнаружили, что, по-видимому, различные теории могут быть объединены математическими преобразованиями, называемыми S-дуальностью и T-дуальностью . Гипотеза Виттена была основана частично на существовании этих дуальностей и частично на связи теорий струн с теорией поля, называемой одиннадцатимерной супергравитацией .
Хотя полная формулировка М-теории неизвестна, такая формулировка должна описывать двух- и пятимерные объекты, называемые бранами , и должна быть аппроксимирована одиннадцатимерной супергравитацией при низких энергиях . Современные попытки сформулировать М-теорию обычно основаны на матричной теории или соответствии AdS/CFT . Согласно Виттену, М должно означать «магия», «тайна» или «мембрана» в зависимости от вкуса, а истинное значение названия должно быть определено, когда будет известна более фундаментальная формулировка теории. [1]
Исследования математической структуры М-теории породили важные теоретические результаты в физике и математике. Более спекулятивно, М-теория может предоставить основу для разработки единой теории всех фундаментальных сил природы. Попытки связать М-теорию с экспериментом обычно фокусируются на компактификации ее дополнительных измерений для построения моделей-кандидатов четырехмерного мира, хотя до сих пор ни одна из них не была проверена, чтобы дать начало физике, наблюдаемой в экспериментах по физике высоких энергий .
Фон
Квантовая гравитация и струны

Одной из самых глубоких проблем современной физики является проблема квантовой гравитации . Современное понимание гравитации основано на общей теории относительности Альберта Эйнштейна , которая сформулирована в рамках классической физики . Однако негравитационные силы описываются в рамках квантовой механики , радикально иного формализма для описания физических явлений, основанного на вероятности . [a] Квантовая теория гравитации необходима для того, чтобы примирить общую теорию относительности с принципами квантовой механики, [b] но трудности возникают, когда кто-то пытается применить обычные предписания квантовой теории к силе гравитации. [c]
Теория струн — это теоретическая структура , которая пытается примирить гравитацию и квантовую механику. В теории струн точечные частицы физики частиц заменяются одномерными объектами, называемыми струнами . Теория струн описывает, как струны распространяются в пространстве и взаимодействуют друг с другом. В данной версии теории струн существует только один вид струны, которая может выглядеть как небольшая петля или сегмент обычной струны, и она может вибрировать по-разному. На масштабах расстояний, больших, чем масштаб струны, струна будет выглядеть так же, как обычная частица, с ее массой , зарядом и другими свойствами, определяемыми вибрационным состоянием струны. Таким образом, все различные элементарные частицы можно рассматривать как вибрирующие струны. Одно из вибрационных состояний струны порождает гравитон , квантово-механическую частицу, которая переносит гравитационную силу. [d]
Существует несколько версий теории струн: тип I , тип IIA , тип IIB и два варианта гетеротической теории струн ( SO (32) и E 8 × E 8 ). Различные теории допускают различные типы струн, а частицы, возникающие при низких энергиях, демонстрируют различные симметрии . Например, теория типа I включает как открытые струны (которые являются сегментами с конечными точками), так и закрытые струны (которые образуют замкнутые петли), в то время как типы IIA и IIB включают только замкнутые струны. [2] Каждая из этих пяти теорий струн возникает как особый предельный случай М-теории. Эта теория, как и ее предшественники в теории струн, является примером квантовой теории гравитации. Она описывает силу, похожую на знакомую гравитационную силу, подчиняющуюся правилам квантовой механики. [3]
Количество измерений

В повседневной жизни существуют три привычных измерения пространства: высота, ширина и глубина. Общая теория относительности Эйнштейна рассматривает время как измерение наравне с тремя пространственными измерениями; в общей теории относительности пространство и время не моделируются как отдельные сущности, а вместо этого объединяются в четырехмерное пространство-время , три пространственных измерения и одно временное измерение. В этой структуре явление гравитации рассматривается как следствие геометрии пространства-времени. [4]
Несмотря на то, что Вселенная хорошо описывается четырехмерным пространством-временем, есть несколько причин, по которым физики рассматривают теории в других измерениях. В некоторых случаях, моделируя пространство-время в другом количестве измерений, теория становится более математически понятной, и можно выполнять вычисления и получать общие идеи легче. [e] Существуют также ситуации, когда теории в двух или трех измерениях пространства-времени полезны для описания явлений в физике конденсированного состояния . [5] Наконец, существуют сценарии, в которых на самом деле может быть более четырех измерений пространства-времени, которые, тем не менее, сумели избежать обнаружения. [6]
Одной из примечательных особенностей теории струн и М-теории является то, что эти теории требуют дополнительных измерений пространства-времени для своей математической согласованности. В теории струн пространство-время десятимерно (девять пространственных измерений и одно временное измерение),в то время как в М-теории он одиннадцатимерный (десять пространственных измерений и одно временное измерение). Для того чтобы описать реальные физические явления с помощью этих теорий, нужно представить себе сценарии, в которых эти дополнительные измерения не будут наблюдаться в экспериментах. [7]
Компактификация — один из способов изменения числа измерений в физической теории. [f] При компактификации предполагается, что некоторые из дополнительных измерений «замыкаются» на себе, образуя окружности. [8] В пределе, когда эти свернутые измерения становятся очень маленькими, получается теория, в которой пространство-время фактически имеет меньшее число измерений. Стандартной аналогией для этого является рассмотрение многомерного объекта, такого как садовый шланг. Если шланг смотреть с достаточного расстояния, кажется, что он имеет только одно измерение — длину. Однако, приближаясь к шлангу, обнаруживаешь, что он содержит второе измерение — окружность. Таким образом, муравей, ползущий по поверхности шланга, будет двигаться в двух измерениях. [g]
Дуальности
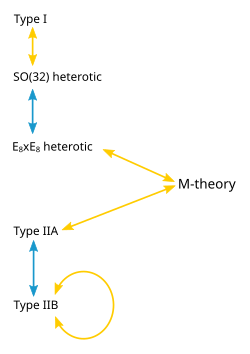
Теории, возникающие как различные пределы М-теории, оказываются связанными весьма нетривиальным образом. Одно из соотношений, которое может существовать между этими различными физическими теориями, называется S-дуальностью . Это соотношение гласит, что совокупность сильно взаимодействующих частиц в одной теории в некоторых случаях может рассматриваться как совокупность слабо взаимодействующих частиц в совершенно другой теории. Грубо говоря, совокупность частиц считается сильно взаимодействующей, если они часто объединяются и распадаются, и слабо взаимодействующей, если они делают это нечасто. Теория струн типа I оказывается эквивалентной по S-дуальности гетеротической теории струн SO (32) . Аналогично, теория струн типа IIB связана сама с собой нетривиальным образом по S-дуальности. [10]
Другое соотношение между различными теориями струн — это T-дуальность . Здесь рассматриваются струны, распространяющиеся вокруг кругового дополнительного измерения. T-дуальность утверждает, что струна, распространяющаяся вокруг окружности радиуса R , эквивалентна струне, распространяющейся вокруг окружности радиуса 1/ R в том смысле, что все наблюдаемые величины в одном описании отождествляются с величинами в дуальном описании. Например, струна имеет импульс , когда она распространяется вокруг окружности, и она также может обмотаться вокруг окружности один или несколько раз. Количество раз, которое струна обматывается вокруг окружности, называется числом намотки . Если струна имеет импульс p и число намотки n в одном описании, она будет иметь импульс n и число намотки p в дуальном описании. Например, теория струн типа IIA эквивалентна теории струн типа IIB посредством T-дуальности, и две версии гетеротической теории струн также связаны посредством T-дуальности. [10]
В общем, термин дуальность относится к ситуации, когда две, казалось бы, разные физические системы оказываются эквивалентными нетривиальным образом. Если две теории связаны дуальностью, это означает, что одна теория может быть преобразована каким-то образом так, что в итоге она будет выглядеть точно так же, как другая теория. Тогда говорят, что две теории дуальны друг другу при преобразовании. Иными словами, две теории являются математически разными описаниями одних и тех же явлений. [11]
Суперсимметрия
Другая важная теоретическая идея, которая играет роль в М-теории, — это суперсимметрия . Это математическое соотношение, которое существует в некоторых физических теориях между классом частиц, называемых бозонами , и классом частиц, называемых фермионами . Грубо говоря, фермионы являются составными частями материи, в то время как бозоны опосредуют взаимодействия между частицами. В теориях с суперсимметрией каждый бозон имеет аналог, который является фермионом, и наоборот. Когда суперсимметрия накладывается как локальная симметрия, автоматически получается квантово-механическая теория, которая включает гравитацию. Такая теория называется теорией супергравитации . [12]
Теория струн, включающая идею суперсимметрии, называется теорией суперструн . Существует несколько различных версий теории суперструн, которые все включены в рамки М-теории. При низких энергиях теории суперструн аппроксимируются одной из трех супергравитаций в десяти измерениях, известных как супергравитация типа I , типа IIA и типа IIB . Аналогично, М-теория аппроксимируется при низких энергиях супергравитацией в одиннадцати измерениях. [3]
Браны
В теории струн и связанных с ней теориях, таких как теории супергравитации, брана — это физический объект, который обобщает понятие точечной частицы на более высокие измерения. Например, точечную частицу можно рассматривать как брану размерности ноль, в то время как струну можно рассматривать как брану размерности один. Также можно рассматривать браны более высоких измерений. В размерности p они называются p -бранами. Браны — это динамические объекты, которые могут распространяться в пространстве-времени в соответствии с правилами квантовой механики. Они могут иметь массу и другие атрибуты, такие как заряд. P -брана выметает ( p + 1) -мерный объем в пространстве-времени, называемый ее мировым объемом . Физики часто изучают поля, аналогичные электромагнитному полю , которые живут в мировом объеме браны. Слово брана происходит от слова «мембрана», которое относится к двумерной бране. [13]
В теории струн фундаментальными объектами, дающими начало элементарным частицам, являются одномерные струны. Хотя физические явления, описываемые М-теорией, все еще плохо изучены, физики знают, что теория описывает двух- и пятимерные браны. Большая часть современных исследований в области М-теории направлена на то, чтобы лучше понять свойства этих бран. [h]
История и развитие
Теория Калуцы–Клейна
В начале 20-го века физики и математики, включая Альберта Эйнштейна и Германа Минковского, были пионерами использования четырехмерной геометрии для описания физического мира. [14] Эти усилия достигли кульминации в формулировке общей теории относительности Эйнштейна, которая связывает гравитацию с геометрией четырехмерного пространства-времени. [15]
Успех общей теории относительности привел к попыткам применить геометрию более высоких измерений для объяснения других сил. В 1919 году работа Теодора Калуцы показала, что, перейдя к пятимерному пространству-времени, можно объединить гравитацию и электромагнетизм в одну силу. [15] Эта идея была улучшена физиком Оскаром Клейном , который предположил, что дополнительное измерение, предложенное Калуцой, может иметь форму круга с радиусом около 10−30 см. [ 16]
Теория Калуцы-Клейна и последующие попытки Эйнштейна разработать единую теорию поля никогда не были полностью успешными. Отчасти это было связано с тем, что теория Калуцы-Клейна предсказала частицу (радион ) , существование которой никогда не было доказано, а отчасти потому, что она не могла правильно предсказать отношение массы электрона к его заряду. Кроме того, эти теории разрабатывались как раз тогда, когда другие физики начинали открывать квантовую механику, которая в конечном итоге оказалась успешной в описании известных сил, таких как электромагнетизм, а также новых ядерных сил , которые были открыты в середине века. Таким образом, потребовалось почти пятьдесят лет, чтобы идея новых измерений снова была воспринята всерьез. [17]
Ранние работы по супергравитации

Новые концепции и математические инструменты дали свежий взгляд на общую теорию относительности, положив начало периоду в 1960–1970-х годах, который теперь известен как золотой век общей теории относительности . [18] В середине 1970-х годов физики начали изучать многомерные теории, объединяющие общую теорию относительности с суперсимметрией, так называемые теории супергравитации. [19]
Общая теория относительности не накладывает никаких ограничений на возможные измерения пространства-времени. Хотя теория обычно формулируется в четырех измерениях, можно записать те же уравнения для гравитационного поля в любом количестве измерений. Супергравитация более ограничительна, поскольку она накладывает верхний предел на количество измерений. [12] В 1978 году работа Вернера Нама показала, что максимальное измерение пространства-времени, в котором можно сформулировать последовательную суперсимметричную теорию, равно одиннадцати. [20] В том же году Эжен Креммер , Бернар Жюлиа и Джоэль Шерк из Высшей нормальной школы показали, что супергравитация не только допускает до одиннадцати измерений, но и является наиболее элегантной в этом максимальном количестве измерений. [21] [22]
Первоначально многие физики надеялись, что компактификацией одиннадцатимерной супергравитации можно будет построить реалистичные модели нашего четырехмерного мира. Надежда была в том, что такие модели предоставят единое описание четырех фундаментальных сил природы: электромагнетизма, сильных и слабых ядерных сил и гравитации. Интерес к одиннадцатимерной супергравитации вскоре угас, поскольку были обнаружены различные недостатки в этой схеме. Одна из проблем заключалась в том, что законы физики, по-видимому, различают по часовой стрелке и против часовой стрелки, явление, известное как хиральность . Эдвард Виттен и другие наблюдали, что это свойство хиральности не может быть легко получено путем компактификации из одиннадцати измерений. [22]
В первой суперструнной революции в 1984 году многие физики обратились к теории струн как к единой теории физики частиц и квантовой гравитации. В отличие от теории супергравитации, теория струн смогла учесть хиральность стандартной модели и предоставила теорию гравитации, согласующуюся с квантовыми эффектами. [22] Еще одной особенностью теории струн, которая привлекла многих физиков в 1980-х и 1990-х годах, была ее высокая степень уникальности. В обычных теориях частиц можно рассматривать любую совокупность элементарных частиц, классическое поведение которых описывается произвольным лагранжианом . В теории струн возможности гораздо более ограничены: к 1990-м годам физики утверждали, что существует только пять последовательных суперсимметричных версий теории. [22]
Взаимосвязи между теориями струн
Хотя существовало лишь несколько последовательных теорий суперструн, оставалось загадкой, почему не было только одной последовательной формулировки. [22] Однако, когда физики начали более внимательно изучать теорию струн, они поняли, что эти теории связаны сложным и нетривиальным образом. [23]
В конце 1970-х годов Клаус Монтонен и Дэвид Олив предположили особое свойство некоторых физических теорий. [24] Уточненная версия их гипотезы касается теории, называемой N = 4 суперсимметричной теорией Янга–Миллса , которая описывает теоретические частицы, формально подобные кваркам и глюонам , из которых состоят атомные ядра . Сила, с которой взаимодействуют частицы этой теории, измеряется числом, называемым константой связи . Результат Монтонена и Олива, теперь известный как дуальность Монтонена–Оливы , утверждает, что N = 4 суперсимметричная теория Янга–Миллса с константой связи g эквивалентна той же теории с константой связи 1/ g . Другими словами, система сильно взаимодействующих частиц (большая константа связи) имеет эквивалентное описание как система слабо взаимодействующих частиц (малая константа связи) и наоборот [25] с помощью спинового момента.
В 1990-х годах несколько теоретиков обобщили дуальность Монтонена–Олива до отношения S-дуальности, которое связывает различные теории струн. Ашок Сен изучал S-дуальность в контексте гетеротических струн в четырех измерениях. [26] [27] Крис Халл и Пол Таунсенд показали, что теория струн типа IIB с большой константой связи эквивалентна посредством S-дуальности той же теории с малой константой связи. [28] Теоретики также обнаружили, что различные теории струн могут быть связаны посредством T-дуальности. Эта дуальность подразумевает, что струны, распространяющиеся в совершенно разных геометриях пространства-времени, могут быть физически эквивалентны. [29]
Мембраны и пятибраны
Теория струн расширяет обычную физику частиц, заменяя нульмерные точечные частицы одномерными объектами, называемыми струнами. В конце 1980-х годов для теоретиков было естественно попытаться сформулировать другие расширения, в которых частицы заменяются двумерными супермембранами или многомерными объектами, называемыми бранами. Такие объекты рассматривались еще в 1962 году Полем Дираком [30] , и они были пересмотрены небольшой, но энтузиастичной группой физиков в 1980-х годах. [22]
Суперсимметрия строго ограничивает возможное число измерений браны. В 1987 году Эрик Бергшофф, Эргин Сезгин и Пол Таунсенд показали, что одиннадцатимерная супергравитация включает двумерные браны. [31] Интуитивно эти объекты выглядят как листы или мембраны, распространяющиеся через одиннадцатимерное пространство-время. Вскоре после этого открытия Майкл Дафф , Пол Хоу, Такео Инами и Келлог Стелле рассмотрели конкретную компактификацию одиннадцатимерной супергравитации, в которой одно из измерений свернуто в круг. [32] В этой обстановке можно представить себе мембрану, оборачивающуюся вокруг кругового измерения. Если радиус круга достаточно мал, то эта мембрана выглядит как струна в десятимерном пространстве-времени. Фактически, Дафф и его коллеги показали, что эта конструкция воспроизводит в точности струны, появляющиеся в теории суперструн типа IIA. [25]
В 1990 году Эндрю Строминджер опубликовал аналогичный результат, который предполагал, что сильно взаимодействующие струны в десяти измерениях могут иметь эквивалентное описание в терминах слабо взаимодействующих пятимерных бран. [33] Первоначально физики не могли доказать эту связь по двум важным причинам. С одной стороны, дуальность Монтонена–Олива все еще не была доказана, и поэтому гипотеза Строминджера была еще более слабой. С другой стороны, существовало много технических проблем, связанных с квантовыми свойствами пятимерных бран. [34] Первая из этих проблем была решена в 1993 году, когда Ашок Сен установил, что определенные физические теории требуют существования объектов как с электрическим , так и с магнитным зарядом, которые были предсказаны в работе Монтонена и Олива. [35]
Несмотря на этот прогресс, связь между струнами и пятимерными бранами оставалась предположительной, поскольку теоретики не могли квантовать браны. Начиная с 1991 года группа исследователей, в которую входили Майкл Дафф, Рамзи Хури, Цзяньсинь Лу и Рубен Минасян, рассматривала специальную компактификацию теории струн, в которой четыре из десяти измерений сворачиваются. Если рассмотреть пятимерную брану, обернутую вокруг этих дополнительных измерений, то брана будет выглядеть как одномерная струна. Таким образом, предполагаемая связь между струнами и бранами была сведена к связи между струнами и струнами, и последняя могла быть проверена с использованием уже установленных теоретических методов. [29]
Вторая суперструнная революция

Выступая на конференции по теории струн в Университете Южной Калифорнии в 1995 году, Эдвард Виттен из Института перспективных исследований сделал неожиданное предположение, что все пять теорий суперструн на самом деле являются просто различными предельными случаями одной теории в одиннадцати измерениях пространства-времени. Заявление Виттена объединило все предыдущие результаты по S- и T-дуальности и появлению двух- и пятимерных бран в теории струн. [36] В течение месяцев после заявления Виттена в Интернете появились сотни новых статей, подтверждающих, что новая теория вовлекает мембраны в важный аспект. [37] Сегодня этот поток работ известен как вторая суперструнная революция . [38]
Одним из важных событий после заявления Виттена была работа Виттена в 1996 году с теоретиком струн Петром Горжавой . [39] [40] Виттен и Горжава изучали М-теорию на специальной геометрии пространства-времени с двумя десятимерными граничными компонентами. Их работа пролила свет на математическую структуру М-теории и предложила возможные пути соединения М-теории с физикой реального мира. [41]
Происхождение термина
Первоначально некоторые физики предположили, что новая теория является фундаментальной теорией мембран, но Виттен скептически отнесся к роли мембран в этой теории. В статье 1996 года Хоржава и Виттен написали
Поскольку было высказано предположение, что одиннадцатимерная теория является теорией супермембраны, но есть некоторые причины сомневаться в такой интерпретации, мы будем необязательно называть ее М-теорией, оставляя на будущее связь М с мембранами. [39]
В отсутствие понимания истинного значения и структуры М-теории Виттен предположил, что М должно означать «магия», «тайна» или «мембрана» по вкусу, а истинное значение названия должно быть определено, когда станет известна более фундаментальная формулировка теории. [1] Годы спустя он заявил: «Я думал, что мои коллеги поймут, что на самом деле это означает мембрана. К сожалению, это сбивало людей с толку». [42]
Теория матриц
Матричная модель BFSS
В математике матрица — это прямоугольный массив чисел или других данных. В физике матричная модель — это особый вид физической теории, математическая формулировка которой включает в себя понятие матрицы важным образом. Матричная модель описывает поведение набора матриц в рамках квантовой механики. [43] [44]
Одним из важных [ почему? ] примеров матричной модели является матричная модель BFSS, предложенная Томом Бэнксом , Вилли Фишлером , Стивеном Шенкером и Леонардом Сасскиндом в 1997 году. Эта теория описывает поведение набора из девяти больших матриц. В своей оригинальной статье эти авторы показали, среди прочего, что предел низкой энергии этой матричной модели описывается одиннадцатимерной супергравитацией. Эти вычисления привели их к предположению, что матричная модель BFSS в точности эквивалентна М-теории. Поэтому матричная модель BFSS может быть использована в качестве прототипа для правильной формулировки М-теории и инструмента для исследования свойств М-теории в относительно простой обстановке. [43] [ необходимо разъяснение ]
Некоммутативная геометрия
В геометрии часто бывает полезно ввести координаты . Например, чтобы изучить геометрию евклидовой плоскости , определяют координаты x и y как расстояния между любой точкой на плоскости и парой осей . В обычной геометрии координаты точки являются числами, поэтому их можно умножать, а произведение двух координат не зависит от порядка умножения. То есть, xy = yx . Это свойство умножения известно как коммутативный закон , и эта связь между геометрией и коммутативной алгеброй координат является отправной точкой для большей части современной геометрии. [45]
Некоммутативная геометрия — это раздел математики, который пытается обобщить эту ситуацию. Вместо того, чтобы работать с обычными числами, мы рассматриваем некоторые похожие объекты, такие как матрицы, умножение которых не удовлетворяет коммутативному закону (то есть объекты, для которых xy не обязательно равно yx ). Мы представляем, что эти некоммутативные объекты являются координатами в некотором более общем понятии «пространства» и доказываем теоремы об этих обобщенных пространствах, используя аналогию с обычной геометрией. [46]
В статье 1998 года Ален Коннес , Майкл Р. Дуглас и Альберт Шварц показали, что некоторые аспекты матричных моделей и М-теории описываются некоммутативной квантовой теорией поля , особым видом физической теории, в которой координаты в пространстве-времени не удовлетворяют свойству коммутативности. [44] Это установило связь между матричными моделями и М-теорией, с одной стороны, и некоммутативной геометрией, с другой стороны. Это быстро привело к открытию других важных связей между некоммутативной геометрией и различными физическими теориями. [47] [48]
Соответствие AdS/CFT
Обзор

Применение квантовой механики к физическим объектам, таким как электромагнитное поле, которые распространяются в пространстве и времени, известно как квантовая теория поля . [i] В физике элементарных частиц квантовые теории поля формируют основу для нашего понимания элементарных частиц, которые моделируются как возбуждения в фундаментальных полях. Квантовые теории поля также используются в физике конденсированных сред для моделирования частицеподобных объектов, называемых квазичастицами . [j]
Один из подходов к формулировке М-теории и изучению ее свойств обеспечивается соответствием анти-де Ситтера/конформной теории поля (AdS/CFT) . Предложенное Хуаном Малдасеной в конце 1997 года, соответствие AdS/CFT является теоретическим результатом, который подразумевает, что М-теория в некоторых случаях эквивалентна квантовой теории поля. [49] Помимо предоставления информации о математической структуре струн и М-теории, соответствие AdS/CFT пролило свет на многие аспекты квантовой теории поля в режимах, где традиционные вычислительные методы неэффективны. [50]
В соответствии с AdS/CFT геометрия пространства-времени описывается в терминах определенного вакуумного решения уравнения Эйнштейна, называемого анти-де-ситтеровским пространством . [51] В очень элементарных терминах анти-де-ситтеровское пространство — это математическая модель пространства-времени, в которой понятие расстояния между точками (метрика ) отличается от понятия расстояния в обычной евклидовой геометрии . Оно тесно связано с гиперболическим пространством , которое можно рассматривать как диск , как показано слева. [52] На этом изображении показана мозаика диска треугольниками и квадратами. Можно определить расстояние между точками этого диска таким образом, что все треугольники и квадраты будут иметь одинаковый размер, а круговая внешняя граница будет бесконечно далека от любой точки внутри. [53]

Теперь представьте себе стопку гиперболических дисков, где каждый диск представляет состояние Вселенной в данный момент времени. Полученный геометрический объект — трехмерное антидеситтеровское пространство. [52] Оно выглядит как сплошной цилиндр , в котором любое поперечное сечение является копией гиперболического диска. Время на этой картинке течет вдоль вертикального направления. Поверхность этого цилиндра играет важную роль в соответствии AdS/CFT. Как и в случае с гиперболической плоскостью, антидеситтеровское пространство искривлено таким образом, что любая точка внутри фактически бесконечно далека от этой граничной поверхности. [53]
Эта конструкция описывает гипотетическую вселенную с двумя пространственными измерениями и одним временным измерением, но ее можно обобщить на любое количество измерений. Действительно, гиперболическое пространство может иметь более двух измерений, и можно «складывать» копии гиперболического пространства, чтобы получить более многомерные модели анти-де-ситтеровского пространства. [52]
Важной особенностью пространства анти-де Ситтера является его граница (которая выглядит как цилиндр в случае трехмерного пространства анти-де Ситтера). Одним из свойств этой границы является то, что в пределах небольшой области на поверхности вокруг любой заданной точки она выглядит точно так же, как пространство Минковского , модель пространства-времени, используемая в негравитационной физике. [54] Поэтому можно рассмотреть вспомогательную теорию, в которой «пространство-время» задается границей пространства анти-де Ситтера. Это наблюдение является отправной точкой для соответствия AdS/CFT, которое утверждает, что граница пространства анти-де Ситтера может рассматриваться как «пространство-время» для квантовой теории поля. Утверждается, что эта квантовая теория поля эквивалентна теории гравитации на объемном пространстве анти-де Ситтера в том смысле, что существует «словарь» для перевода сущностей и вычислений в одной теории в их аналоги в другой теории. Например, отдельная частица в теории гравитации может соответствовать некоторому набору частиц в граничной теории. Кроме того, предсказания в двух теориях количественно идентичны, так что если две частицы имеют 40-процентный шанс столкновения в гравитационной теории, то соответствующие совокупности в граничной теории также будут иметь 40-процентный шанс столкновения. [55]
6D (2,0) суперконформная теория поля

Одна из частных реализаций соответствия AdS/CFT утверждает, что M-теория на пространстве произведений AdS 7 × S 4 эквивалентна так называемой (2,0)-теории на шестимерной границе. [49] Здесь «(2,0)» относится к конкретному типу суперсимметрии, которая появляется в теории. В этом примере пространство-время гравитационной теории фактически является семимерным (отсюда обозначение AdS 7 ), и есть четыре дополнительных « компактных » измерения (закодированных фактором S 4 ). В реальном мире пространство-время является четырехмерным, по крайней мере макроскопически, поэтому эта версия соответствия не обеспечивает реалистичную модель гравитации. Аналогично, дуальная теория не является жизнеспособной моделью любой системы реального мира, поскольку она описывает мир с шестью пространственно-временными измерениями. [k]
Тем не менее, (2,0)-теория оказалась важной для изучения общих свойств квантовых теорий поля. Действительно, эта теория включает в себя много математически интересных эффективных квантовых теорий поля и указывает на новые дуальности, связывающие эти теории. Например, Луис Алдай, Давиде Гайотто и Юджи Тачикава показали, что путем компактификации этой теории на поверхности получается четырехмерная квантовая теория поля, и существует дуальность, известная как соответствие AGT , которая связывает физику этой теории с определенными физическими концепциями, связанными с самой поверхностью. [56] Совсем недавно теоретики расширили эти идеи для изучения теорий, полученных путем компактификации до трех измерений. [57]
В дополнение к своим приложениям в квантовой теории поля, (2,0)-теория породила важные результаты в чистой математике . Например, существование (2,0)-теории было использовано Виттеном, чтобы дать «физическое» объяснение для предполагаемого отношения в математике, называемого геометрическим соответствием Ленглендса . [58] В последующей работе Виттен показал, что (2,0)-теория может быть использована для понимания концепции в математике, называемой гомологией Хованова . [59] Разработанная Михаилом Ховановым около 2000 года, гомология Хованова предоставляет инструмент в теории узлов , разделе математики, который изучает и классифицирует различные формы узлов. [60] Другим применением (2,0)-теории в математике является работа Давиде Гайотто , Грега Мура и Эндрю Нейцке , которые использовали физические идеи для получения новых результатов в гиперкэлеровой геометрии . [61]
ABJM суперконформная теория поля
Другая реализация соответствия AdS/CFT утверждает, что M-теория на AdS 4 × S 7 эквивалентна квантовой теории поля, называемой теорией ABJM в трех измерениях. В этой версии соответствия семь измерений M-теории свернуты, оставляя четыре некомпактных измерения. Поскольку пространство-время нашей Вселенной четырехмерно, эта версия соответствия обеспечивает несколько более реалистичное описание гравитации. [62]
Теория ABJM, представленная в этой версии соответствия, также интересна по ряду причин. Введенная Ахарони, Бергманом, Джафферисом и Малдасеной, она тесно связана с другой квантовой теорией поля, называемой теорией Черна–Саймонса . Последняя теория была популяризирована Виттеном в конце 1980-х годов из-за ее приложений к теории узлов. [63] Кроме того, теория ABJM служит полуреалистичной упрощенной моделью для решения проблем, возникающих в физике конденсированного состояния. [62]
Феноменология
Обзор

Помимо того, что М-теория представляет значительный теоретический интерес, она обеспечивает основу для построения моделей физики реального мира, которые объединяют общую теорию относительности со стандартной моделью физики элементарных частиц . Феноменология — это раздел теоретической физики, в котором физики строят реалистичные модели природы из более абстрактных теоретических идей. Феноменология струн — это часть теории струн, которая пытается построить реалистичные модели физики элементарных частиц на основе теории струн и М-теории. [64]
Обычно такие модели основаны на идее компактификации. [l] Начиная с десяти- или одиннадцатимерного пространства-времени струнной или М-теории, физики постулируют форму для дополнительных измерений. Выбрав эту форму соответствующим образом, они могут построить модели, примерно похожие на стандартную модель физики элементарных частиц, вместе с дополнительными неоткрытыми частицами, [65] обычно суперсимметричными партнерами аналогов известных частиц. Один из популярных способов вывода реалистичной физики из теории струн — начать с гетеротической теории в десяти измерениях и предположить, что шесть дополнительных измерений пространства-времени имеют форму шестимерного многообразия Калаби-Яу . Это особый вид геометрического объекта, названного в честь математиков Эухенио Калаби и Шинг-Тунг Яу . [66] Многообразия Калаби-Яу предлагают много способов извлечения реалистичной физики из теории струн. Другие подобные методы могут быть использованы для построения моделей с физикой, в некоторой степени напоминающей физику нашего четырехмерного мира, основанного на М-теории. [67]
Частично из-за теоретических и математических трудностей, а частично из-за чрезвычайно высоких энергий (за пределами того, что технологически возможно в обозримом будущем), необходимых для экспериментальной проверки этих теорий, до сих пор нет экспериментальных доказательств, которые бы однозначно указывали на то, что любая из этих моделей является правильным фундаментальным описанием природы. Это привело к тому, что некоторые в сообществе стали критиковать эти подходы к объединению и усомнились в ценности продолжения исследований по этим проблемам. [68]
Компактификация наГ 2коллекторы
В одном из подходов к феноменологии М-теории теоретики предполагают, что семь дополнительных измерений М-теории имеют форму многообразия G2 . Это особый вид семимерной формы, созданный математиком Домиником Джойсом из Оксфордского университета . [69] Эти многообразия G2 до сих пор плохо изучены математически, и этот факт затруднил для физиков полную разработку этого подхода к феноменологии. [70]
Например, физики и математики часто предполагают, что пространство имеет математическое свойство, называемое гладкостью , но это свойство не может быть предположено в случае многообразия G 2 , если кто-то хочет восстановить физику нашего четырехмерного мира. Другая проблема заключается в том, что многообразия G 2 не являются комплексными многообразиями , поэтому теоретики не могут использовать инструменты из раздела математики, известного как комплексный анализ . Наконец, существует много открытых вопросов о существовании, уникальности и других математических свойствах многообразий G 2 , и математикам не хватает систематического способа поиска этих многообразий. [70]
Гетеротическая М-теория
Из-за трудностей с многообразиями G 2 большинство попыток построить реалистичные теории физики на основе М-теории использовали более косвенный подход к компактификации одиннадцатимерного пространства-времени. Один подход, впервые предложенный Виттеном, Хоравой, Буртом Оврутом и другими, известен как гетеротическая М-теория. В этом подходе предполагается, что одно из одиннадцати измерений М-теории имеет форму круга. Если этот круг очень мал, то пространство-время становится фактически десятимерным. Затем предполагается, что шесть из десяти измерений образуют многообразие Калаби-Яу. Если это многообразие Калаби-Яу также считается малым, то остается теория в четырех измерениях. [70]
Гетеротическая М-теория использовалась для построения моделей бранной космологии , в которых наблюдаемая вселенная, как полагают, существует на бране в более многомерном окружающем пространстве. Она также породила альтернативные теории ранней вселенной, которые не опираются на теорию космической инфляции . [70]
Ссылки
Примечания
- ^ Стандартное введение в квантовую механику см. в Griffiths 2004.
- ^ Необходимость квантово-механического описания гравитации следует из того факта, что невозможно последовательно связать классическую систему с квантовой. См. Wald 1984, стр. 382.
- ^ С технической точки зрения проблема в том, что теория, полученная таким образом, не перенормируема и, следовательно, не может быть использована для осмысленных физических предсказаний. См. Zee 2010, стр. 72 для обсуждения этого вопроса.
- ^ Доступное введение в теорию струн см. в Greene 2000.
- ^ Например, в контексте соответствия AdS/CFT теоретики часто формулируют и изучают теории гравитации в нефизических числах измерений пространства-времени.
- ^ Уменьшение размерности — это еще один способ изменения количества измерений.
- ^ Эта аналогия используется, например, в Greene 2000, стр. 186.
- ^ Например, см. подразделы о 6D (2,0) суперконформной теории поля и ABJM суперконформной теории поля .
- ^ Стандартный текст — Пескин и Шредер 1995.
- ^ Введение в применение квантовой теории поля в физике конденсированного состояния см. в Zee 2010.
- ^ Обзор (2,0)-теории см. в Moore 2012.
- ^ Сценарии мира браны предоставляют альтернативный способ восстановления физики реального мира из теории струн. См. Randall and Sundrum 1999.
Цитаты
- ^ ab Duff 1996, раздел 1
- ^ Цвибах 2009, стр. 324
- ^ ab Беккер, Беккер и Шварц 2007, стр. 12
- ^ Вальд 1984, стр. 4
- ^ Zee 2010, Части V и VI
- ^ Цвибах 2009, стр. 9
- ^ Цвибах 2009, стр. 8
- ^ Яу и Надис 2010, Гл. 6
- ^ Беккер, Беккер и Шварц 2007, стр. 339–347.
- ^ ab Беккер, Беккер и Шварц 2007
- ^ Цвибах 2009, стр. 376
- ^ ab Duff 1998, стр. 64
- ^ Мур 2005
- ^ Яу и Надис 2010, стр. 9
- ^ Аб Яу и Надис 2010, с. 10
- ^ Яу и Надис 2010, стр. 12
- ^ Яу и Надис 2010, стр. 13
- ^ Вальд 1984, стр. 3
- ^ ван Ньювенхейзен 1981
- ^ Нам 1978
- ^ Креммер, Джулия и Шерк 1978
- ^ abcdef Дафф 1998, стр. 65
- ^ Дафф 1998
- ^ Монтонен и Олив 1977
- ^ ab Duff 1998, стр. 66
- ^ Сен 1994a
- ^ Сен 1994b
- ^ Халл и Таунсенд 1995
- ^ ab Duff 1998, стр. 67
- ^ Дирак 1962
- ^ Бергшофф, Сезгин и Таунсенд 1987
- ^ Дафф и др. 1987
- ^ Стромингер 1990
- ^ Дафф 1998, стр. 66–67
- ^ Сен 1993
- ^ Виттен 1995
- ^ Дафф 1998, стр. 67–68.
- ^ Беккер, Беккер и Шварц 2007, стр. 296
- ^ ab Hořava и Witten 1996a
- ^ Хоржава и Виттен 1996b
- ^ Дафф 1998, стр. 68
- ^ Гефтер, Аманда (2014). Нарушение границ на лужайке Эйнштейна: Отец, дочь, смысл ничего и начало всего . Random House. ISBN 978-0-345-531438.в 345
- ^ ab Banks и др. 1997
- ^ аб Конн, Дуглас и Шварц, 1998 г.
- ^ Коннес 1994, стр. 1
- ^ Конн 1994
- ^ Некрасов и Шварц 1998
- ^ Зайберг и Виттен 1999
- ^ ab Maldacena 1998
- ^ Клебанов и Малдасена 2009
- ^ Клебанов и Малдасена 2009, с. 28
- ^ abc Maldacena 2005, стр. 60
- ^ ab Maldacena 2005, стр. 61
- ^ Цвибах 2009, стр. 552
- ^ Малдасена 2005, стр. 61–62
- ^ Алдай, Гайотто и Тачикава, 2010 г.
- ^ Димофте, Гайотто и Гуков, 2010 г.
- ^ Виттен 2009
- ^ Виттен 2012
- ^ Хованов 2000
- ^ Гайотто, Мур и Нейтцке 2013
- ^ ab Ахарони и др. 2008
- ^ Виттен 1989
- ^ Дайн 2000
- ^ Канделас и др. 1985
- ^ Яу и Надис 2010, стр. ix
- ^ Яу и Надис 2010, стр. 147–150.
- ^ Войт 2006
- ^ Яу и Надис 2010, стр. 149
- ^ abcd Яу и Надис 2010, с. 150
Библиография
- Ахарони, Офер; Бергман, Орен; Джафферис, Дэниел Луис ; Малдасена, Хуан (2008). " N =6 суперконформные теории материи Черна-Саймонса, M2-браны и их гравитационные дуалы". Журнал физики высоких энергий . 2008 (10): 091. arXiv : 0806.1218 . Bibcode : 2008JHEP...10..091A. doi : 10.1088/1126-6708/2008/10/091. S2CID 16987793.
- Alday, Luis; Gaiotto, Davide; Tachikawa, Yuji (2010). «Корреляционные функции Лиувилля из четырехмерных калибровочных теорий». Письма в математическую физику . 91 (2): 167–197. arXiv : 0906.3219 . Bibcode :2010LMaPh..91..167A. doi :10.1007/s11005-010-0369-5. S2CID 15459761.
- Бэнкс, Том; Фишлер, Вилли; Шенкер, Стивен; Сасскинд, Леонард (1997). «Теория М как матричная модель: гипотеза». Physical Review D. 55 ( 8): 5112–5128. arXiv : hep-th/9610043 . Bibcode : 1997PhRvD..55.5112B. doi : 10.1103/physrevd.55.5112. S2CID 13073785.
- Беккер, Катрин; Беккер, Мелани ; Шварц, Джон (2007). Теория струн и М-теория: современное введение . Cambridge University Press. ISBN 978-0-521-86069-7.
- Бергшофф, Эрик; Сезгин, Эргин; Таунсенд, Пол (1987). «Супермембраны и одиннадцатимерная супергравитация» (PDF) . Physics Letters B . 189 (1): 75–78. Bibcode :1987PhLB..189...75B. doi :10.1016/0370-2693(87)91272-X. S2CID 123289423.
- Канделас, Филипп; Горовиц, Гари; Стромингер, Эндрю; Виттен, Эдвард (1985). «Вакуумные конфигурации для суперструн». Nuclear Physics B. 258 : 46–74. Bibcode : 1985NuPhB.258...46C. doi : 10.1016/0550-3213(85)90602-9.
- Конн, Ален (1994). Некоммутативная геометрия . Academic Press. ISBN 978-0-12-185860-5.
- Конн, Ален; Дуглас, Майкл; Шварц, Альберт (1998). "Некоммутативная геометрия и теория матриц". Журнал физики высоких энергий . 19981 (2): 003. arXiv : hep-th/9711162 . Bibcode : 1998JHEP...02..003C. doi : 10.1088/1126-6708/1998/02/003. S2CID 7562354.
- Креммер, Юджин; Джулия, Бернард; Шерк, Джоэль (1978). «Теория супергравитации в одиннадцати измерениях». Physics Letters B. 76 ( 4): 409–412. Bibcode : 1978PhLB...76..409C. doi : 10.1016/0370-2693(78)90894-8.
- Dimofte, Tudor; Gaiotto, Davide; Gukov, Sergey (2010). "Gauge theories labeled by three-manifolds" (Калибровочные теории, помеченные трехмерными многообразиями). Communications in Mathematical Physics . 325 (2): 367–419. arXiv : 1108.4389 . Bibcode : 2014CMaPh.325..367D. doi : 10.1007/s00220-013-1863-2. S2CID 10882599. Архивировано из оригинала 2020-09-18 . Получено 2017-07-04 .
- Дайн, Майкл (2000). «Лекции TASI по феноменологии теории М». Струны, браны и гравитация : 545–612. arXiv : hep-th/0003175 . doi :10.1142/9789812799630_0006. ISBN 978-981-02-4774-4. S2CID 17851652.
- Дирак, Поль (1962). «Расширяемая модель электрона». Труды Лондонского королевского общества . A. Математические и физические науки. 268 (1332): 57–67. Bibcode : 1962RSPSA.268...57D. doi : 10.1098/rspa.1962.0124. S2CID 122728729.
- Дафф, Майкл (1996). «М-теория (теория, ранее известная как струны)». International Journal of Modern Physics A . 11 (32): 6523–41. arXiv : hep-th/9608117 . Bibcode :1996IJMPA..11.5623D. doi :10.1142/S0217751X96002583. S2CID 17432791.
- Дафф, Майкл (1998). «Теория, ранее известная как струны». Scientific American . 278 (2): 64–9. Bibcode : 1998SciAm.278b..64D. doi : 10.1038/scientificamerican0298-64.
- Дафф, Майкл; Хоу, Пол; Инами, Такео; Стелле, Келлог (1987). «Суперструны в D=10 из супермембран в D=11». Nuclear Physics B . 191 (1): 70–74. Bibcode :1987PhLB..191...70D. doi :10.1016/0370-2693(87)91323-2.
- Gaiotto, Davide; Moore, Gregory; Neitzke, Andrew (2013). «Пересечение стены, системы Хитчина и приближение WKB». Advances in Mathematics . 234 : 239–403. arXiv : 0907.3987 . doi : 10.1016/j.aim.2012.09.027 .
- Грин, Брайан (2000). Элегантная Вселенная: Суперструны, Скрытые Измерения и Поиски Окончательной Теории . Random House. ISBN 978-0-9650888-0-0.
- Гриффитс, Дэвид (2004). Введение в квантовую механику . Pearson Prentice Hall. ISBN 978-0-13-111892-8.
- Хоржава, Петр; Виттен, Эдвард (1996a). «Гетеротическая и струнная динамика типа I из одиннадцати измерений». Nuclear Physics B . 460 (3): 506–524. arXiv : hep-th/9510209 . Bibcode :1996NuPhB.460..506H. doi :10.1016/0550-3213(95)00621-4. S2CID 17028835.
- Хоржава, Петр; Виттен, Эдвард (1996b). «Одиннадцатимерная супергравитация на многообразии с границей». Nuclear Physics B . 475 (1): 94–114. arXiv : hep-th/9603142 . Bibcode :1996NuPhB.475...94H. doi :10.1016/0550-3213(96)00308-2. S2CID 16122181.
- Халл, Крис; Таунсенд, Пол (1995). «Единство дуальностей суперструн». Nuclear Physics B . 4381 (1): 109–137. arXiv : hep-th/9410167 . Bibcode :1995NuPhB.438..109H. doi :10.1016/0550-3213(94)00559-W. S2CID 13889163.
- Хованов, Михаил (2000). «Категоризация многочлена Джонса». Duke Mathematical Journal . 1011 (3): 359–426. arXiv : math/9908171 . doi :10.1215/S0012-7094-00-10131-7. S2CID 119585149.
- Клебанов, Игорь; Малдасена, Хуан (2009). "Решение квантовых теорий поля с помощью искривленных пространств-времен" (PDF) . Physics Today . 62 (1): 28. Bibcode :2009PhT....62a..28K. doi : 10.1063/1.3074260 . Архивировано из оригинала 2010-06-10.
{{cite journal}}: CS1 maint: bot: original URL status unknown (link) - Малдасена, Хуан (1998). «Большой предел N суперконформных теорий поля и супергравитации». Успехи теоретической и математической физики . 2 (2): 231–252. arXiv : hep-th/9711200 . Bibcode :1998AdTMP...2..231M. doi :10.4310/ATMP.1998.V2.N2.A1.
- Maldacena, Juan (2005). «Иллюзия гравитации» (PDF) . Scientific American . 293 (5): 56–63. Bibcode :2005SciAm.293e..56M. doi :10.1038/scientificamerican1105-56. PMID 16318027. Архивировано из оригинала 2013-11-10.
{{cite journal}}: CS1 maint: bot: original URL status unknown (link) - Монтонен, Клаус; Олив, Дэвид (1977). «Магнитные монополи как калибровочные частицы?». Physics Letters B. 72 ( 1): 117–120. Bibcode : 1977PhLB...72..117M. doi : 10.1016/0370-2693(77)90076-4.
- Мур, Грегори (2005). «Что такое ... брана?» (PDF) . Notices of the AMS . 52 : 214. Получено 6 августа 2016 г.
- Мур, Грегори (2012). "Конспект лекций Феликса Кляйна" (PDF) . Получено 14 августа 2013 .
- Нам, Уолтер (1978). «Суперсимметрии и их представления». Nuclear Physics B. 135 ( 1): 149–166. Bibcode : 1978NuPhB.135..149N. doi : 10.1016/0550-3213(78)90218-3.
- Некрасов, Никита; Шварц, Альберт (1998). «Инстантоны на некоммутативном R 4 и (2,0) суперконформная шестимерная теория». Сообщения по математической физике . 198 (3): 689–703. arXiv : hep-th/9802068 . Bibcode :1998CMaPh.198..689N. doi :10.1007/s002200050490. S2CID 14125789.
- Пескин, Майкл; Шредер, Дэниел (1995). Введение в квантовую теорию поля . Westview Press. ISBN 978-0-201-50397-5.
- Рэндалл, Лиза; Сандрум, Раман (1999). «Альтернатива компактификации». Physical Review Letters . 83 (23): 4690–4693. arXiv : hep-th/9906064 . Bibcode :1999PhRvL..83.4690R. doi :10.1103/PhysRevLett.83.4690. S2CID 18530420.
- Зайберг, Натан; Виттен, Эдвард (1999). «Теория струн и некоммутативная геометрия». Журнал физики высоких энергий . 1999 (9): 032. arXiv : hep-th/9908142 . Bibcode : 1999JHEP...09..032S. doi : 10.1088/1126-6708/1999/09/032. S2CID 668885.
- Сен, Ашок (1993). «Электромагнитная дуальность в теории струн». Nuclear Physics B. 404 ( 1): 109–126. arXiv : hep-th/9207053 . Bibcode : 1993NuPhB.404..109S. doi : 10.1016/0550-3213(93)90475-5. S2CID 18887335.
- Сен, Ашок (1994a). «Дуальность сильной-слабой связи в четырехмерной теории струн». International Journal of Modern Physics A . 9 (21): 3707–3750. arXiv : hep-th/9402002 . Bibcode :1994IJMPA...9.3707S. doi :10.1142/S0217751X94001497. S2CID 16706816.
- Сен, Ашок (1994b). «Связанные состояния дайона-монополя, самодуальные гармонические формы на пространстве модулей мультимонополя и инвариантность SL (2, Z ) в теории струн». Physics Letters B . 329 (2): 217–221. arXiv : hep-th/9402032 . Bibcode :1994PhLB..329..217S. doi :10.1016/0370-2693(94)90763-3. S2CID 17534677.
- Стромингер, Эндрю (1990). «Гетеротические солитоны». Nuclear Physics B. 343 ( 1): 167–184. Bibcode : 1990NuPhB.343..167S. doi : 10.1016/0550-3213(90)90599-9.
- ван Ньювенхейзен, Питер (1981). «Супергравитация». Отчеты по физике . 68 (4): 189–398. Бибкод : 1981PhR....68..189В. дои : 10.1016/0370-1573(81)90157-5.
- Уолд, Роберт (1984). Общая теория относительности . Издательство Чикагского университета. ISBN 978-0-226-87033-5.
- Виттен, Эдвард (1989). «Квантовая теория поля и многочлен Джонса». Сообщения по математической физике . 121 (3): 351–399. Bibcode : 1989CMaPh.121..351W. doi : 10.1007/BF01217730. MR 0990772. S2CID 14951363.
- Виттен, Эдвард (1995). «Динамика теории струн в различных измерениях». Nuclear Physics B. 443 ( 1): 85–126. arXiv : hep-th/9503124 . Bibcode : 1995NuPhB.443...85W. doi : 10.1016/0550-3213(95)00158-O. S2CID 16790997.
- Виттен, Эдвард (2009). «Геометрические Ленгленды из шести измерений». arXiv : 0905.2720 [hep-th].
- Виттен, Эдвард (2012). «Пятибраны и узлы». Квантовая топология . 3 (1): 1–137. arXiv : 1101.3216 . doi :10.4171/QT/26. S2CID 119248828.
- Woit, Peter (2006). Даже не неправильно: провал теории струн и поиск единства в физическом законе . Basic Books. стр. 105. ISBN 0-465-09275-6.
- Яу, Шинг-Тунг; Надис, Стив (2010). Форма внутреннего пространства: теория струн и геометрия скрытых измерений Вселенной . Базовые книги. ISBN 978-0-465-02023-2.
- Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Princeton University Press. ISBN 978-0-691-14034-6.
- Цвибах, Бартон (2009). Первый курс теории струн . Cambridge University Press. ISBN 978-0-521-88032-9.
Популяризация
- BBC Horizon: «Параллельные вселенные» — полнометражный документальный фильм 2002 года от BBC Horizon , эпизод «Параллельные вселенные» посвящен истории и возникновению М-теории, а также ученым, принимавшим в ней участие.
- [1] PBS.org-NOVA: The Elegant Universe ] – удостоенный премии «Эмми» 2003 года трехчасовой мини-сериал от Nova с Брайаном Грином , адаптированный по его книге The Elegant Universe (первоначальные даты трансляции на PBS : 28 октября, 20:00–22:00 и 4 ноября, 20:00–21:00, 2003)
Смотрите также
Внешние ссылки
- Superstringtheory.com – «Официальный веб-сайт теории струн», созданный Патрисией Шварц. Ссылки по теории струн и М-теории для неспециалистов и экспертов.
- Not Even Wrong – блог Питера Войта о физике в целом и теории струн в частности.
- М-теория - Эдвард Виттен (1995) - лекция Виттена 1995 года, в которой он вводит М-теорию.