Перекрестная энтропия
| Теория информации |
|---|
 |
В теории информации перекрестная энтропия между двумя распределениями вероятностей и для одного и того же базового набора событий измеряет среднее число бит, необходимое для идентификации события, взятого из набора, когда схема кодирования, используемая для набора, оптимизирована для предполагаемого распределения вероятностей , а не для истинного распределения .
Определение
Перекрестная энтропия распределения относительно распределения по заданному набору определяется следующим образом:
где — оператор ожидаемого значения относительно распределения .
Определение можно сформулировать с помощью дивергенции Кульбака–Лейблера , дивергенции от (также известной как относительная энтропия по отношению к ).
где - энтропия .
Для дискретных распределений вероятностей и с той же поддержкой это означает
( Уравнение 1 )
Аналогичная ситуация для непрерывных распределений. Мы должны предположить, что и абсолютно непрерывны относительно некоторой референтной меры (обычно это мера Лебега на борелевской σ-алгебре ). Пусть и будут функциями плотности вероятности и относительно . Тогда
и поэтому
( Уравнение 2 )
Примечание: эта нотация также используется для другого понятия — совместной энтропии и .
Мотивация
В теории информации теорема Крафта-Макмиллана устанавливает, что любая непосредственно декодируемая схема кодирования для кодирования сообщения для идентификации одного значения из набора возможностей может рассматриваться как представление неявного распределения вероятностей по , где — длина кода для в битах. Таким образом, кросс-энтропия может быть интерпретирована как ожидаемая длина сообщения на единицу данных, когда предполагается неправильное распределение, в то время как данные фактически следуют распределению . Вот почему ожидание берется по истинному распределению вероятностей , а не Действительно, ожидаемая длина сообщения при истинном распределении равна
Оценка
Существует много ситуаций, когда необходимо измерить кросс-энтропию, но распределение неизвестно. Примером является моделирование языка , где модель создается на основе обучающего набора , а затем ее кросс-энтропия измеряется на тестовом наборе, чтобы оценить, насколько точна модель в прогнозировании тестовых данных. В этом примере — истинное распределение слов в любом корпусе, а — распределение слов, предсказанное моделью. Поскольку истинное распределение неизвестно, кросс-энтропия не может быть рассчитана напрямую. В этих случаях оценка кросс-энтропии рассчитывается с использованием следующей формулы:
где — размер тестового набора, а — вероятность события, оцененная по обучающему набору. Другими словами, — оценка вероятности модели того, что i-е слово текста — это . Сумма усредняется по словам теста. Это оценка Монте-Карло истинной кросс-энтропии, где тестовый набор рассматривается как выборки из . [ необходима цитата ]
Отношение к максимальному правдоподобию
Перекрестная энтропия возникает в задачах классификации при введении логарифма под видом логарифмической функции правдоподобия .
Раздел посвящен теме оценки вероятности различных возможных дискретных результатов. Для этого обозначим параметризованное семейство распределений как , с учетом усилий по оптимизации. Рассмотрим заданную конечную последовательность значений из обучающего набора, полученную из условно независимой выборки. Правдоподобие, назначенное любому рассматриваемому параметру модели, затем задается произведением по всем вероятностям . Возможны повторные появления, что приводит к равным факторам в произведении. Если количество появлений значения, равного (для некоторого индекса ), обозначено как , то частота этого значения равна . Обозначим последнее как , так как это можно понимать как эмпирическое приближение к распределению вероятностей, лежащему в основе сценария. Далее обозначим через недоумение , которое можно увидеть равным по правилам расчета для логарифма , и где произведение находится по значениям без двойного счета. Так или Поскольку логарифм является монотонно возрастающей функцией , он не влияет на экстремизацию. Поэтому заметим, что максимизация правдоподобия сводится к минимизации перекрестной энтропии.
Минимизация кросс-энтропии
Минимизация кросс-энтропии часто используется в оптимизации и оценке вероятности редких событий. При сравнении распределения с фиксированным эталонным распределением кросс-энтропия и дивергенция KL идентичны с точностью до аддитивной константы (поскольку фиксировано): Согласно неравенству Гиббса , оба принимают минимальные значения, когда , что соответствует дивергенции KL, и для кросс-энтропии. В инженерной литературе принцип минимизации дивергенции KL (Кульбакский « Принцип минимальной дискриминационной информации ») часто называют принципом минимальной кросс-энтропии (MCE) или Minxent .
Однако, как обсуждалось в статье Расхождение Кульбака–Лейблера , иногда распределение является фиксированным априорным референтным распределением, и распределение оптимизируется, чтобы быть как можно ближе к нему, при условии некоторого ограничения. В этом случае две минимизации не эквивалентны. Это привело к некоторой двусмысленности в литературе, и некоторые авторы пытались разрешить несоответствие, переформулируя кросс-энтропию как , а не . Фактически, кросс-энтропия — это еще одно название относительной энтропии ; см. Cover и Thomas [1] и Good. [2] С другой стороны, не согласуется с литературой и может вводить в заблуждение.
Функция кросс-энтропийных потерь и логистическая регрессия
Перекрестная энтропия может использоваться для определения функции потерь в машинном обучении и оптимизации . Мао, Мори и Чжун (2023) дают обширный анализ свойств семейства функций потерь перекрестной энтропии в машинном обучении, включая теоретические гарантии обучения и расширения для состязательного обучения . [3] Истинная вероятность является истинной меткой, а заданное распределение является прогнозируемым значением текущей модели. Это также известно как логарифмические потери (или логарифмические потери [4] или логистические потери ); [5] термины «логарифмические потери» и «потери перекрестной энтропии» используются взаимозаменяемо. [6]
Более конкретно, рассмотрим бинарную регрессионную модель, которая может быть использована для классификации наблюдений на два возможных класса (часто просто обозначенных и ). Выходные данные модели для данного наблюдения, заданного вектором входных признаков , можно интерпретировать как вероятность, которая служит основой для классификации наблюдения. В логистической регрессии вероятность моделируется с использованием логистической функции , где — некоторая функция входного вектора , обычно просто линейная функция. Вероятность выходных данных задается как , где вектор весов оптимизируется с помощью некоторого подходящего алгоритма, такого как градиентный спуск . Аналогично, дополнительная вероятность нахождения выходных данных просто задается как
Установив наши обозначения и , мы можем использовать перекрестную энтропию, чтобы получить меру различия между и :

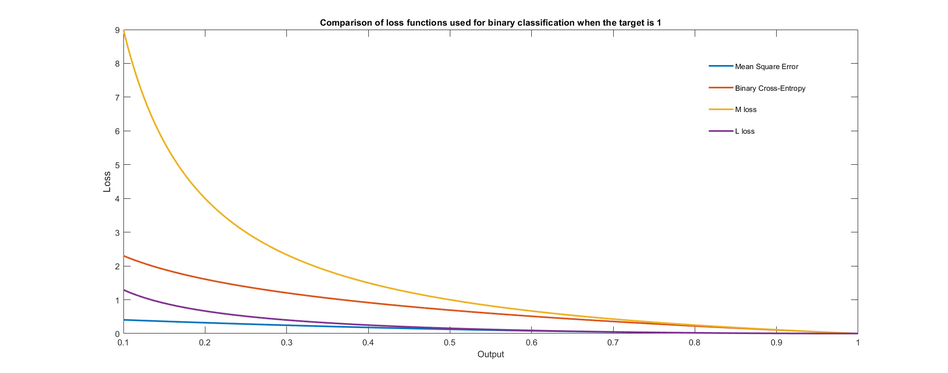
На графике показаны различные функции потерь, которые можно использовать для обучения бинарного классификатора. Показан только случай, когда целевой выход равен 1. Замечено, что потеря равна нулю, когда целевой выход равен выходу, и увеличивается по мере того, как выход становится все более неверным.
Логистическая регрессия обычно оптимизирует логарифм потерь для всех наблюдений, на которых она обучается, что то же самое, что и оптимизация средней перекрестной энтропии в выборке. Другие функции потерь, которые штрафуют ошибки по-разному, также могут использоваться для обучения, что приводит к моделям с различной конечной точностью теста. [7] Например, предположим, что у нас есть выборки, каждая из которых индексирована на . Среднее значение функции потерь тогда определяется как:
где , с логистической функцией, как и прежде.
Логистическая потеря иногда называется кросс-энтропийной потерей. Она также известна как логарифмическая потеря. [ дублирование? ] (В этом случае бинарная метка часто обозначается как {−1,+1}. [8] )
Замечание: Градиент потери кросс-энтропии для логистической регрессии такой же, как градиент потери квадратичной ошибки для линейной регрессии . То есть, определим
Тогда у нас есть результат
Доказательство следующее. Для любого имеем
Подобным образом мы в конечном итоге получаем желаемый результат.
Измененная кросс-энтропия
Может быть полезно обучить ансамбль моделей, которые имеют разнообразие, так что при их объединении увеличивается их предсказательная точность. [9] [10] Предполагая, что простой ансамбль классификаторов собирается путем усреднения выходов, тогда измененная перекрестная энтропия задается как , где — функция стоимости классификатора , — вероятность выхода классификатора , — истинная вероятность, которая должна быть оценена, и — параметр между 0 и 1, который определяет «разнообразие», которое мы хотели бы установить среди ансамбля. Когда мы хотим, чтобы каждый классификатор делал все возможное независимо от ансамбля, и когда мы хотели бы, чтобы классификатор был максимально разнообразным.
Смотрите также
- Метод кросс-энтропии
- Логистическая регрессия
- Условная энтропия
- Расстояние Кульбака–Лейблера
- Оценка максимального правдоподобия
- Взаимная информация
- Недоумение
Ссылки
- ^ Томас М. Кавер, Джой А. Томас, Элементы теории информации, 2-е издание, Wiley, стр. 80
- ^ IJ Good, Максимальная энтропия для формулировки гипотез, особенно для многомерных таблиц сопряженности, Ann. of Math. Statistics, 1963
- ^ Аньци Мао, Мехриар Мохри, Ютао Чжун. Функции потери кросс-энтропии: теоретический анализ и приложения. ICML 2023. https://arxiv.org/pdf/2304.07288.pdf
- ^ Математика кодирования, извлечения и распределения информации , Джордж Цибенко, Дайан П. О'Лири, Йорма Риссанен, 1999, стр. 82
- ^ Вероятность для машинного обучения: узнайте, как использовать неопределенность с помощью Python , Джейсон Браунли, 2019, стр. 220: «Логистические потери относятся к функции потерь, обычно используемой для оптимизации модели логистической регрессии. Их также могут называть логарифмическими потерями (что сбивает с толку) или просто логарифмическими потерями».
- ^ sklearn.metrics.log_loss
- ^ Ноэль, Мэтью; Банерджи, Ариндам; Д, Джеральдин Бесси Амали; Мутиа-Накараджан, Венкатараман (17 марта 2023 г.). «Альтернативные функции потерь для классификации и надежной регрессии могут повысить точность искусственных нейронных сетей». arXiv : 2303.09935 [cs.NE].
- ^ Мерфи, Кевин (2012). Машинное обучение: вероятностная перспектива . MIT. ISBN 978-0262018029.
- ^ Шохам, Рон; Пермутер, Хаим Х. (2019). «Измененная стоимость кросс-энтропии: подход к поощрению разнообразия в ансамбле классификации (краткое объявление)». В Долев, Шломи; Хендлер, Дэнни; Лодха, Сачин; Юнг, Моти (ред.). Кибербезопасность, криптография и машинное обучение – Третий международный симпозиум, CSCML 2019, Беэр-Шева, Израиль, 27–28 июня 2019 г., Труды . Конспект лекций по информатике. Том 11527. Springer. стр. 202–207. doi :10.1007/978-3-030-20951-3_18. ISBN 978-3-030-20950-6.
- ^ Шохам, Рон; Пермутер, Хаим (2020). «Измененная стоимость перекрестной энтропии: структура для явного поощрения разнообразия». arXiv : 2007.08140 [cs.LG].
Дальнейшее чтение
- де Бур, Крез, Д.П., Маннор, С. и Рубинштейн, Р.Ю. (2005). Учебное пособие по методу кросс-энтропии. Annals of Operations Research 134 (1), 19–67.


![{\displaystyle H(p,q)=-\operatorname {E} _{p}[\log q],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268ca3c9c9fe130daec06698c3b5f5f3fdabc45b)
![{\displaystyle E_{p}[\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d16c30a1e4e78c3714c3aed9cd48f7f1990441a9)








![{\displaystyle -\int _{\mathcal {X}}P(x)\,\log Q(x)\,\mathrm {d} x=\operatorname {E} _{p}[-\log Q] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f9b06c86a803a0cd88d1303b6b22c5dcc5e8182)







![{\displaystyle \operatorname {E} _{p}[\ell ]=-\operatorname {E} _{p}\left[{\frac {\ln {q(x)}}{\ln(2)}}\right]=-\operatorname {E} _{p}\left[\log _{2}{q(x)}\right]=-\sum _{x_{i}}p(x_{i})\,\log _{2}q(x_{i})=-\sum _{x}p(x)\,\log _{2}q(x)=H(p,q).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5427081785e1c503a5e3c49969c38d8d90c21a)



































![{\displaystyle J(\mathbf {w})\ =\ {\frac {1}{N}}\sum _{n=1}^{N}H(p_{n},q_{n})\ = \ -{\frac {1}{N}}\sum _{n=1}^{N}\ {\bigg [}y_{n}\log {\hat {y}}_{n}+(1-y_{n})\log(1- {\hat {y}}_{n}){\bigg ]}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58b5509fc3ee46e5aabb134b095d316dcb462796)




![{\displaystyle L({\boldsymbol {\beta }})=-\sum _{i=1}^{N}\left[y_{i}\log {\hat {y}}_{i}+(1-y_{i})\log(1-{\hat {y}}_{i})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4853978e83348b07e0b3c80d3152d7bbdeb30211)




![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial \beta _{0}}}L({\boldsymbol {\beta }})&=-\sum _{i=1}^{N}\left[{\frac {y_{i}\cdot e^{-\beta _{0}+k_{0}}}{1+e^{-\beta _{0}+k_{0}}}}-(1-y_{i}){\frac {1}{1+e^{-\beta _{0}+k_{0}}}}\right]\\&=-\sum _{i=1}^{N}\left[y_{i}-{\hat {y}}_{i}\right]=\sum _{i=1}^{N}({\hat {y}}_{i}-y_{i}),\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da12a84826141abda49405406ae48a367606398f)

![{\displaystyle {\frac {\partial }{\partial \beta _{1}}}\ln \left[1-{\frac {1}{1+e^{-\beta _{1}x_{i1}+k_{1}}}}\right]={\frac {-x_{i1}e^{\beta _{1}x_{i1}}}{e^{\beta _{1}x_{i1}}+e^{k_{1}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f551d787c499daded9a2cb523f6025d802bf491e)








