Теорема Лохса

В теории чисел теорема Лохса касается скорости сходимости разложения в цепную дробь типичного действительного числа. Доказательство теоремы было опубликовано в 1964 году Густавом Лохсом. ^[1]

Теорема утверждает, что для почти всех действительных чисел в интервале (0,1) число членов m цепной дроби числа, необходимых для определения первых n знаков десятичной дроби числа, ведет себя асимптотически следующим образом:

${\displaystyle \lim _{n\to \infty }{\frac {m}{n}}={\frac {6\ln(2)\ln(10)}{\pi ^{2}}}\approx 0,97027014}$(последовательность A086819 в OEIS ). ^[2]

Поскольку этот предел лишь немного меньше 1, это можно интерпретировать как то, что каждый дополнительный член в представлении непрерывной дроби "типичного" действительного числа увеличивает точность представления примерно на один десятичный знак. Десятичная система является последней позиционной системой , в которой каждая цифра несет меньше информации, чем одно частное непрерывной дроби; переход к основанию 11 (изменение на в уравнении) заставляет указанное выше значение превышать 1.${\displaystyle \ln(10)}$${\displaystyle \ln(11)}$

Обратная величина этого предела,

${\displaystyle {\frac {\pi ^{2}}{6\ln(2)\ln(10)}}\приблизительно 1,03064083}$(последовательность A062542 в OEIS ),

это удвоенный десятичный логарифм постоянной Леви .

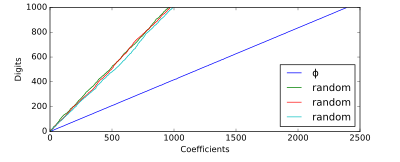
Ярким примером числа, не демонстрирующего такого поведения, является золотое сечение — иногда называемое « самым иррациональным » числом — члены непрерывной дроби которого все являются единицами, наименьшим возможным числом в канонической форме. В среднем для этого требуется приблизительно 2,39 члена непрерывной дроби на десятичную цифру. ^[3]

Доказательство предполагает основные свойства цепных дробей . Пусть — отображение Гаусса.${\displaystyle T:x\mapsto 1/x\mod 1}$

Пусть — функция плотности вероятности для распределения Гаусса, которая сохраняется при отображении Гаусса.${\displaystyle \rho (t)={\frac {1}{(1+t)\ln 2}}}$

Поскольку функция плотности вероятности ограничена сверху и снизу, множество пренебрежимо мало относительно меры Лебега тогда и только тогда, когда оно распределено по Гауссу.

Лемма. .${\textstyle {\frac {1}{n}}\ln T^{n}x\to 0}$

Доказательство. Поскольку , то и только тогда, когда Рассмотрим множество всех , которые имеют . То есть, где обозначает множество чисел, чье разложение в непрерывную дробь имеет , но не имеет других ограничений. Теперь, поскольку отображение Гаусса сохраняет меру Гаусса, имеет ту же меру Гаусса, что и , что то же самое, что и${\textstyle T^{n}x\leq 1}$${\textstyle {\frac {1}{n}}\ln T^{n}x\to 0}$$${\displaystyle \liminf {\frac {1}{n}}\ln T^{n}x=0}$$${\textstyle x}$${\textstyle \liminf {\frac {1}{n}}\ln T^{n}x<0}$$${\displaystyle \{x:\exists c>0,\forall N\geq 1,\exists n\geq N,T^{n}x<e^{-cn}\}}$$ $${\displaystyle =\cup _{c>0}\cap _{N\geq 1}\cup _{n\geq N}[0;\mathbb {N} ,\dots ,\mathbb {N} ,a_{n}>e^{cn},\mathbb {N} ,\dots ]}$$${\displaystyle [0;\mathbb {N} ,\dots ,\mathbb {N} ,a_{n}>e^{cn},\mathbb {N} ,\dots ]}$${\displaystyle a_{n}>e^{cn}}$$${\displaystyle [0;\mathbb {N} ,\dots ,\mathbb {N} ,a_{n}>e^{cn},\mathbb {N} ,\dots ]}$$${\textstyle [0;a_{n}>e^{cn},\mathbb {N} ,\dots ]}$

$${\displaystyle \int _{0}^{e^{-cn}}\rho (t)dt=\log _{2}(1+e^{-cn})\sim {\frac {e^{-cn}}{\ln 2}}}$$Объединение по сумме дает , которая в пределе равна нулю.${\textstyle \cup _{n\geq N}}$${\textstyle \sim {\frac {e^{-cN}}{(1-e^{-c})\ln 2}}}$${\textstyle N\to \infty }$

Таким образом, множество таких имеет нулевую меру Гаусса.${\textstyle x}$

Теперь разложим член, используя основные свойства непрерывной дроби: Второй член — . Третий член — . Оба исчезают после деления на . Таким образом , мы использовали результат константы Леви .$${\displaystyle \ln \left|x-{\frac {p_{n}}{q_{n}}}\right|=\ln {\frac {T^{n}x}{q_{n}(q_{n}+q_{n-1}T^{n}x)}}=-2\ln q_{n}+\ln T^{n}x-\ln \left(1+{\frac {q_{n-1}}{q_{n}}}T^{n}x\right)}$$${\textstyle o(n)}$${\textstyle \in [\ln 1,\ln 2]}$${\displaystyle n}$
$${\displaystyle \lim _{n}{\frac {1}{n}}\ln \left|x-{\frac {p_{n}}{q_{n}}}\right|=-2\lim _{n}{\frac {1}{n}}\ln q_{n}=-{\frac {\pi ^{2}}{6\ln 2}}}$$