Локальные координаты касательной плоскости

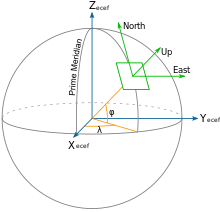
Географическая локальная система координат

Локальные координаты касательной плоскости ( LTP ) являются частью пространственной системы отсчета , основанной на касательной плоскости, определяемой местным вертикальным направлением и осью вращения Земли . Они также известны как локальная эллипсоидальная система , ^[1]^[2] локальная геодезическая система координат , ^[3] локальные вертикальные, локальные горизонтальные координаты ( LVLH ) или топоцентрические координаты . Она состоит из трех координат : одна представляет положение вдоль северной оси, одна вдоль локальной восточной оси и одна представляет вертикальное положение . Существуют два правосторонних варианта: координаты восток, север, вверх ( ENU ) и координаты север, восток, вниз ( NED ). Они служат для представления векторов состояния , которые обычно используются в авиации и морской кибернетике.

Топоры

Эти рамки зависят от местоположения. Для перемещений по всему миру, таких как воздушная или морская навигация, рамки определяются как касательные к линиям географических координат :

Восток-запад, касательная к параллелям ,
Касательная к меридианам с севера на юг , и
Вверх-вниз в направлении, нормальном к сплющенному сфероиду, используемому в качестве земного эллипсоида , который обычно не проходит через центр Земли.

Местные координаты восток, север, верх (ENU)

Во многих приложениях наведения и отслеживания местная декартова система координат Восток, Север, Вверх (ENU) гораздо более интуитивна и практична, чем ECEF или геодезические координаты. Локальные координаты ENU формируются из плоскости, касательной к поверхности Земли, зафиксированной в определенном месте, и поэтому ее иногда называют «локальной касательной» или «локальной геодезической» плоскостью. По соглашению восточная ось обозначается , северная и верхняя . $x$ $у$ $z$

Местные координаты север, восток, низ (NED)

В самолете большинство объектов интереса находятся под самолетом, поэтому разумно определить down как положительное число. Координаты North, East, Down (NED) позволяют использовать это в качестве альтернативы ENU. По соглашению северная ось обозначается , восточная и нижняя . Чтобы избежать путаницы между и и т. д. в этой статье мы ограничим локальную систему координат ENU. $x'$ $y'$ $z'$ $x$ $x'$

Начало этой системы координат обычно выбирается как фиксированная точка на поверхности геоида ниже центра тяжести самолета. В этом случае система координат иногда называется «локальной системой координат северо-восток-вниз». ^[4]

Координаты NED похожи на ECEF в том, что они являются декартовыми, однако они могут быть более удобными из-за относительно небольших задействованных чисел, а также из-за интуитивно понятных осей. Координаты NED и ECEF можно связать с помощью следующей формулы:

\mathbf {p} _{\mathrm {NED} }=R(\mathbf {p} _{\mathrm {ECEF} }-\mathbf {p} _{\mathrm {Ref} })

где — трехмерное положение в системе NED, — соответствующее положение ECEF, — опорное положение ECEF (где начинается локальная касательная плоскость), а — матрица вращения, строки которой представляют собой оси север, восток и вниз. может быть удобно определена из широты и долготы, соответствующих : $\mathbf {p} _{\mathrm {NED} }$ $\mathbf {p} _{\mathrm {ECEF} }$ $\mathbf {p} _{\mathrm {Ref} }$ $R$ $R$ $\phi$ $\lambda$ $\mathbf {p} _{\mathrm {Ref} }$

R={\begin{bmatrix}-\sin(\phi )\cos(\lambda )&-\sin(\phi )\sin(\lambda )&\cos(\phi )\\-\sin(\lambda )&\cos(\lambda )&0\\-\cos(\phi )\cos(\lambda )&-\cos(\phi )\sin(\lambda )&-\sin(\phi )\end{bmatrix}}

^[5]

Смотрите также

Ссылки

^ Торге, Вольфганг; Мюллер, Юрген (29 мая 2012 г.). Геодезия . ДЕ ГРЮТЕР. дои : 10.1515/9783110250008. ISBN 978-3-11-020718-7.
^ Зеебер, Гюнтер (19 июня 2003 г.). Спутниковая геодезия . Вальтер де Грютер. дои : 10.1515/9783110200089. ISBN 978-3-11-017549-3.
^ "Геодезия". GPS Satellite Surveying . Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc. 2015-04-11. стр. 129–206. doi :10.1002/9781119018612.ch4. ISBN 978-1-119-01861-2.
^ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Беспилотные винтокрылые системы . Springer. стр. 27. ISBN 978-0-85729-634-4.
^ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Беспилотные винтокрылые системы . Springer. стр. 32. ISBN 978-0-85729-634-4.

Эта статья об авиации — заглушка . Вы можете помочь Википедии, расширив ее.

[Torge-1] Торге, Вольфганг; Мюллер, Юрген (29 мая 2012 г.). Геодезия . ДЕ ГРЮТЕР. дои : 10.1515/9783110250008. ISBN 978-3-11-020718-7.

[Seeber-2] Зеебер, Гюнтер (19 июня 2003 г.). Спутниковая геодезия . Вальтер де Грютер. дои : 10.1515/9783110200089. ISBN 978-3-11-017549-3.

[3] "Геодезия". GPS Satellite Surveying . Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc. 2015-04-11. стр. 129–206. doi :10.1002/9781119018612.ch4. ISBN 978-1-119-01861-2.

[4] Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Беспилотные винтокрылые системы . Springer. стр. 27. ISBN 978-0-85729-634-4.

[5] Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Беспилотные винтокрылые системы . Springer. стр. 32. ISBN 978-0-85729-634-4.