Правило наследования

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без источников могут быть оспорены и удалены. Найти источники:  «Правило наследования» – новости  · газеты  · книги  · ученый  · JSTOR ( февраль 2017 г. ) ( Узнайте, как и когда удалять это сообщение )

В теории вероятностей правило последовательности — это формула, введенная в XVIII веке Пьером-Симоном Лапласом при рассмотрении проблемы восхода солнца . ^[1] Эта формула до сих пор используется, в частности, для оценки базовых вероятностей, когда имеется несколько наблюдений или событий, которые вообще не наблюдались в (конечном) наборе данных.

Если мы повторим эксперимент, который, как мы знаем, может привести к успеху или неудаче, n раз независимо друг от друга и получим s успехов и n − s неудач, то какова вероятность того, что следующее повторение будет успешным?

Более абстрактно: если X ₁ , ..., X _{n +1} являются условно независимыми случайными величинами , каждая из которых может принимать значение 0 или 1, то, если мы больше ничего о них не знаем,

${\displaystyle P(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s+1 \over n+2}.}$

Поскольку у нас есть предварительное знание, что мы рассматриваем эксперимент, для которого возможны как успех, так и неудача, наша оценка такова, как если бы мы наверняка наблюдали один успех и одну неудачу еще до того, как начали эксперименты. В некотором смысле мы сделали n  + 2 наблюдений (известных как псевдосчетчики ) с s  + 1 успехами. Хотя это может показаться самым простым и разумным предположением, которое также оказывается верным, оно все равно требует доказательства. Действительно, предположение о псевдосчетчике, равном одному на возможность, является одним из способов обобщения бинарного результата, но имеет неожиданные последствия — см. Обобщение на любое количество возможностей ниже.

Тем не менее, если бы мы не знали с самого начала, что возможны как успех, так и неудача, то нам пришлось бы назначить

${\displaystyle P'(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s \over n}.}$

Но см. Математические подробности ниже для анализа его валидности. В частности, он невалиден, когда , или .${\displaystyle s=0}$${\displaystyle s=n}$

Если количество наблюдений увеличивается и они становятся все более и более похожими, то интуитивно понятно: чем больше у нас данных, тем меньшее значение следует придавать нашей априорной информации.${\displaystyle P}$${\displaystyle P'}$

Лаплас использовал правило следования для расчета вероятности того, что Солнце взойдет завтра, учитывая, что оно всходило каждый день в течение последних 5000 лет. Получается очень большой множитель, приблизительно 5000 × 365,25, что дает шансы около 1 826 200 к 1 в пользу того, что Солнце взойдет завтра.

Однако, как показывают математические детали ниже, основное предположение для использования правила следования будет заключаться в том, что у нас нет никаких предварительных знаний о том, взойдет или не взойдет Солнце завтра, за исключением того, что оно может сделать и то, и другое. Это не относится к восходам солнца.

Лаплас хорошо это знал, и он написал в заключение примера с восходом солнца: «Но это число гораздо больше для того, кто, видя в совокупности явлений принцип, регулирующий дни и времена года, понимает, что ничто в настоящий момент не может остановить его ход». ^[2] Однако Лапласа высмеивали за этот расчет; его оппоненты ^{[ кто? ]} не обратили внимания на это предложение или не поняли его важности. ^[2]

В 1940-х годах Рудольф Карнап исследовал вероятностную теорию индуктивного рассуждения и разработал меры степени подтверждения, которые он рассматривал как альтернативу правилу последовательности Лапласа. ^{[3] [4]} См. также Новая загадка индукции#Карнап .

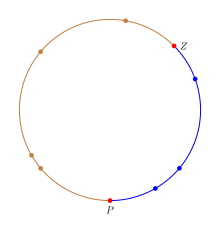
Правило последовательности можно интерпретировать интуитивно, рассматривая точки, случайно распределенные по окружности, а не подсчитывая число «успехов»/«неудач» в эксперименте. ^[5] Чтобы имитировать поведение пропорции p на окружности, мы раскрасим окружность в два цвета, и доля окружности, окрашенная в цвет «успеха», будет равна p . Чтобы выразить неопределенность относительно значения p , нам нужно выбрать долю окружности.

Дробь выбирается путем выбора двух равномерно случайных точек на окружности. Первая точка Z соответствует нулю в интервале [0, 1], а вторая точка P соответствует точке p в пределах [0, 1]. В терминах окружности дробь окружности от Z до P, движущаяся по часовой стрелке, будет равна p . n испытаний можно интерпретировать как n точек, равномерно распределенных на окружности; любая точка в дроби «успеха» является успехом и неудачей в противном случае. Это обеспечивает точное отображение экспериментов «успех/неуспех» с вероятностью успеха p в равномерно случайные точки на окружности. На рисунке дробь успеха окрашена в синий цвет, чтобы отличить ее от остальной части окружности, а точки P и Z выделены красным.

Учитывая этот круг, оценка p — это дробь, окрашенная в синий цвет. Разделим круг на n+2 дуги, соответствующие n+2 точкам, так что часть от точки на круге до следующей точки (движение по часовой стрелке) — это одна дуга, связанная с первой точкой. Таким образом, Z определяет первую синюю дугу, а P определяет первую не синюю/неудачную дугу. Поскольку следующая точка — это равномерно случайная точка, если она попадает в любую из синих дуг, то испытание завершается успешно, а если она попадает в любую из других дуг, то испытание завершается неудачей. Таким образом, вероятность успеха p равна, где b — количество синих дуг, а t — общее количество дуг. Обратите внимание, что синих дуг (дуги Z ) на одну больше, чем точек успеха, и на две дуги (дуги P и Z ) больше, чем n точек. Подстановка значений на количество успехов дает правило последовательности.${\displaystyle {\frac {b}{t}}}$

Примечание: Фактическая вероятность должна использовать длину синих дуг, деленную на длину всех дуг. Однако, когда k точек равномерно распределены по окружности, расстояние от точки до следующей точки равно 1/k. Таким образом, в среднем каждая дуга имеет одинаковую длину, а отношение длин становится отношением количеств.

Пропорции p присваивается равномерное распределение для описания неопределенности относительно ее истинного значения. (Эта пропорция не случайна, а неопределенна. Мы присваиваем p распределение вероятностей , чтобы выразить нашу неопределенность, а не приписывать  p случайность . Но математически это равносильно тому, что рассматривать p так, как если бы оно было случайным).

Пусть X _i будет 1, если мы наблюдаем "успех" в i - м испытании , в противном случае 0, с вероятностью p успеха в каждом испытании. Таким образом, каждое X равно 0 или 1; каждое X имеет распределение Бернулли . Предположим, что эти X условно независимы при заданном p .

Мы можем использовать теорему Байеса , чтобы найти условное распределение вероятностей p, учитывая данные X _i , i = 1, ..., n. Для " априорной " (т.е. предельной) меры вероятности p мы назначили равномерное распределение на открытом интервале (0,1)

${\displaystyle f(p)={\begin{cases}0&{\text{for }}p\leq 0\\1&{\text{for }}0<p<1\\0&{\text{for }}p\geq 1\end{cases}}}$

Для вероятности данного p в наших наблюдениях мы используем функцию правдоподобия

${\displaystyle L(p)=P(X_{1}=x_{1},\ldots ,X_{n}=x_{n}\mid p)=\prod _{i=1}^{n}p^{x_{i}}(1-p)^{1-x_{i}}=p^{s}(1-p)^{n-s}}$

где s  =  x ₁  + ... +  x _n — количество «успехов», а n — количество испытаний (мы используем заглавную букву X для обозначения случайной величины и строчную x для обозначения фактически наблюдаемых данных). Собрав все вместе, мы можем вычислить апостериорную вероятность:

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={L(p)f(p) \over \int _{0}^{1}L(r)f(r)\,dr}={p^{s}(1-p)^{n-s} \over \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr}}$

Чтобы получить нормировочную константу , найдем

${\displaystyle \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr={s!(n-s)! \over (n+1)!}}$

( подробнее об интегралах этой формы см. в бета-функции ).

Следовательно, апостериорная функция плотности вероятности равна

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={(n+1)! \over s!(n-s)!}p^{s}(1-p)^{n-s}.}$

Это бета-распределение с ожидаемым значением

${\displaystyle \operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\int _{0}^{1}pf(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})\,dp={s+1 \over n+2}.}$

Поскольку p говорит нам о вероятности успеха в любом эксперименте, а каждый эксперимент условно независим , условная вероятность успеха в следующем эксперименте равна просто p . Поскольку p рассматривается как случайная величина , закон полной вероятности говорит нам, что ожидаемая вероятность успеха в следующем эксперименте равна просто ожидаемому значению p . Поскольку p зависит от наблюдаемых данных X _i для i = 1, ..., n , мы имеем

${\displaystyle P(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s+1 \over n+2}.}$

Тот же расчет может быть выполнен с (неправильным) априором , который выражает полное незнание p , включая незнание относительно вопроса, может ли эксперимент быть успешным или может потерпеть неудачу. Этот неправильный априор равен 1/( p (1 −  p )) для 0 ≤  p  ≤ 1 и 0 в противном случае. ^[6] Если расчет выше повторить с этим априором, мы получим

${\displaystyle P'(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s \over n}.}$

Таким образом, при предварительном указании полного невежества вероятность успеха регулируется наблюдаемой частотой успеха. Однако апостериорное распределение, которое привело к этому результату, является распределением Beta( s , n  −  s ), которое не является правильным, когда s  =  n или s  = 0 (т. е. константа нормализации бесконечна, когда s  = 0 или s  =  n ). Это означает, что мы не можем использовать эту форму апостериорного распределения для вычисления вероятности того, что следующее наблюдение будет успешным, когда s  = 0 или s  =  n . Это проливает свет на информацию, содержащуюся в правиле последовательности: его можно рассматривать как выражение предварительного предположения о том, что если бы выборка продолжалась бесконечно, мы в конечном итоге наблюдали бы по крайней мере один успех и по крайней мере одну неудачу в выборке. Апостериорное указание полного невежества не предполагает этого знания.

Чтобы оценить случай «полного невежества», когда можно иметь дело с s  = 0 или s  =  n , мы сначала вернемся к гипергеометрическому распределению , обозначенному . Этот подход принят в Jaynes (2003). Биномиальное распределение может быть выведено как предельная форма, где таким образом, что их отношение остается фиксированным. Можно рассматривать как число успехов в общей популяции, размером .${\displaystyle \mathrm {Hyp} (s|N,n,S)}$${\displaystyle \mathrm {Bin} (r|n,p)}$${\displaystyle N,S\rightarrow \infty }$${\displaystyle p={S \over N}}$${\displaystyle S}$${\displaystyle N}$

Эквивалентом до является , с областью определения . Работа с условием до означает, что оценка эквивалентна оценке , а затем делению этой оценки на . Апостериорная величина для может быть задана как:${\displaystyle {1 \over p(1-p)}}$${\displaystyle {1 \over S(N-S)}}$${\displaystyle 1\leq S\leq N-1}$${\displaystyle N}$${\displaystyle p}$${\displaystyle S}$${\displaystyle N}$${\displaystyle S}$

${\displaystyle P(S|N,n,s)\propto {1 \over S(N-S)}{S \choose s}{N-S \choose n-s}\propto {S!(N-S)! \over S(N-S)(S-s)!(N-S-[n-s])!}}$

И можно увидеть, что если s  =  n или s  = 0, то один из факториалов в числителе сокращается ровно на единицу в знаменателе. Принимая случай s  = 0, имеем:

${\displaystyle P(S|N,n,s=0)\propto {(N-S-1)! \over S(N-S-n)!}={\prod _{j=1}^{n-1}(N-S-j) \over S}}$

Добавление нормализующей константы, которая всегда конечна (поскольку в диапазоне апостериорной функции нет сингулярностей, а число членов конечно), дает:

${\displaystyle P(S|N,n,s=0)={\prod _{j=1}^{n-1}(N-S-j) \over S\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Итак, апостериорное ожидание равно:${\displaystyle p={S \over N}}$

${\displaystyle E\left({S \over N}|n,s=0,N\right)={1 \over N}\sum _{S=1}^{N-n}SP(S|N,n=1,s=0)={1 \over N}{\sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j) \over \sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Приблизительное аналитическое выражение для больших N получается путем предварительного приближения к члену произведения:

${\displaystyle \prod _{j=1}^{n-1}(N-R-j)\approx (N-R)^{n-1}}$

а затем заменив сумму в числителе интегралом

${\displaystyle \sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j)\approx \int _{1}^{N-n}(N-S)^{n-1}\,dS={(N-1)^{n}-n^{n} \over n}\approx {N^{n} \over n}}$

Та же процедура применяется к знаменателю, но процесс немного сложнее, поскольку интеграл оценить сложнее.

${\displaystyle {\begin{aligned}\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}&\approx \int _{1}^{N-n}{(N-R)^{n-1} \over R}\,dR\\&=N\int _{1}^{N-n}{(N-R)^{n-2} \over R}\,dR-\int _{1}^{N-n}(N-R)^{n-2}\,dR\\&=N^{n-1}\left[\int _{1}^{N-n}{dR \over R}-{1 \over n-1}+O\left({1 \over N}\right)\right]\approx N^{n-1}\ln(N)\end{aligned}}}$

где ln — натуральный логарифм. Подстановка этих приближений в ожидание дает

${\displaystyle E\left({S \over N}|n,s=0,N\right)\approx {1 \over N}{{N^{n} \over n} \over N^{n-1}\ln(N)}={1 \over n[\ln(N)]}={\log _{10}(e) \over n[\log _{10}(N)]}={0.434294 \over n[\log _{10}(N)]}}$

где логарифм по основанию 10 был использован в окончательном ответе для простоты вычислений. Например, если популяция имеет размер 10 ^k , то вероятность успеха в следующей выборке определяется как:

${\displaystyle E\left({S \over N}\mid n,s=0,N=10^{k}\right)\approx {0.434294 \over nk}}$

Так, например, если популяция составляет порядка десятков миллиардов, так что k  = 10, и мы наблюдаем результаты n  = 10 без успеха, то ожидаемая доля в популяции составляет приблизительно 0,43%. Если популяция меньше, так что n  = 10, k  = 5 (десятки тысяч), ожидаемая доля возрастает приблизительно до 0,86% и т. д. Аналогично, если число наблюдений меньше, так что n  = 5, k  = 10, доля возрастает приблизительно до 0,86% снова.

Эта вероятность не имеет положительной нижней границы и может быть сделана произвольно малой для все большего и большего выбора N или k . Это означает, что вероятность зависит от размера популяции, из которой производится выборка. При переходе к пределу бесконечного N (для более простых аналитических свойств) мы «отбрасываем» часть очень важной информации. Обратите внимание, что это отношение незнания сохраняется только до тех пор, пока не наблюдается ни одного успеха. Оно соответствующим образом пересматривается обратно к правилу наблюдаемой частоты, как только наблюдается один успех. Соответствующие результаты находятся для случая s=n путем переключения меток и последующего вычитания вероятности из 1.${\displaystyle p={s \over n}}$

В этом разделе дается эвристический вывод, аналогичный тому, что приведен в «Теории вероятностей: логика науки» . ^[7]

Правило последовательности имеет много различных интуитивных интерпретаций, и в зависимости от того, какую интуицию вы используете, обобщение может быть разным. Таким образом, отсюда следует действовать очень осторожно и заново выводить результаты из первых принципов, а не вводить интуитивно разумное обобщение. Полный вывод можно найти в книге Джейнса, но он допускает более простой для понимания альтернативный вывод, как только решение известно. Еще один момент, который следует подчеркнуть, заключается в том, что предшествующее состояние знаний, описываемое правилом последовательности, дается как перечисление возможностей с дополнительной информацией о том, что можно наблюдать каждую категорию. Это можно эквивалентно сформулировать как наблюдение каждой категории один раз до сбора данных. Чтобы обозначить, что это используемое знание, I m _{ставится} как часть условий в назначениях вероятности.

Правило наследования исходит из установки биномиального правдоподобия и равномерного априорного распределения. Таким образом, прямое обобщение — это просто многомерные расширения этих двух распределений: 1) Установка равномерного априорного распределения по исходным m категориям и 2) использование полиномиального распределения в качестве функции правдоподобия (что является многомерным обобщением биномиального распределения). Можно показать, что равномерное распределение является частным случаем распределения Дирихле со всеми его параметрами, равными 1 (так же, как равномерное распределение является Beta(1,1) в бинарном случае). Распределение Дирихле является сопряженным априорным распределением для полиномиального распределения, что означает, что апостериорное распределение также является распределением Дирихле с другими параметрами. Пусть p _i обозначает вероятность того, что категория i будет наблюдаться, а n _i обозначает количество раз, которое категория i ( i  = 1, ...,  m ) фактически наблюдалась. Тогда совместное апостериорное распределение вероятностей p ₁ , ...,  p _m задается как:

${\displaystyle f(p_{1},\ldots ,p_{m}\mid n_{1},\ldots ,n_{m},I)={\begin{cases}{\displaystyle {\frac {\Gamma \left(\sum _{i=1}^{m}(n_{i}+1)\right)}{\prod _{i=1}^{m}\Gamma (n_{i}+1)}}p_{1}^{n_{1}}\cdots p_{m}^{n_{m}}},\quad &\sum _{i=1}^{m}p_{i}=1\\\\0&{\text{otherwise.}}\end{cases}}}$

Чтобы получить обобщенное правило последовательности, обратите внимание, что вероятность наблюдения категории i при следующем наблюдении, обусловленная p _{i ,} равна просто p _i , нам просто требуется ее ожидание. Пусть A _i обозначает событие, что следующее наблюдение находится в категории i ( i  = 1, ...,  m ), и пусть n  =  n ₁  + ... +  n _m будет общим числом сделанных наблюдений. Результат, используя свойства распределения Дирихле, будет:

${\displaystyle P(A_{i}|n_{1},\ldots ,n_{m},I_{m})={n_{i}+1 \over n+m}.}$

Это решение сводится к вероятности, которая была бы назначена с использованием принципа безразличия до любых сделанных наблюдений (т.е. n  = 0), в соответствии с исходным правилом наследования. Оно также содержит правило наследования как особый случай, когда m  = 2, как и должно быть в обобщении.

Поскольку предложения или события A _i являются взаимоисключающими, можно свернуть m категорий в 2. Просто сложите вероятности A _i , которые соответствуют «успеху», чтобы получить вероятность успеха. Предположим, что это объединяет c категорий как «успех» и mc категорий как «неудача». Пусть s обозначает сумму соответствующих значений n _i , которые были названы «успехом». Вероятность «успеха» в следующем испытании тогда равна:

${\displaystyle P({\text{success}}|n_{1},\ldots ,n_{m},I_{m})={s+c \over n+m},}$

что отличается от исходного правила наследования. Но обратите внимание, что исходное правило наследования основано на I ₂ , тогда как обобщение основано на I _m . Это означает, что информация, содержащаяся в I _m , отличается от содержащейся в I ₂ . Это указывает на то, что простое знание более чем двух результатов, которые, как мы знаем, возможны, является релевантной информацией при сворачивании этих категорий до двух. Это иллюстрирует тонкость описания априорной информации и то, почему важно указывать, какую априорную информацию мы используем.

Хорошая модель необходима (т. е. хороший компромисс между точностью и практичностью). Перефразируя Лапласа о проблеме восхода солнца : хотя у нас есть огромное количество примеров восходящего солнца, существуют гораздо лучшие модели солнца, чем предполагать, что оно имеет определенную вероятность восхода каждый день, например, просто имея период полураспада.

При наличии хорошей модели лучше всего провести как можно больше наблюдений, в зависимости от ожидаемой надежности предшествующих знаний, стоимости наблюдений, доступного времени и ресурсов, а также требуемой точности.

Одним из самых сложных аспектов правила последовательности являются не математические формулы, а ответ на вопрос: когда применяется правило последовательности? В разделе обобщения это было отмечено очень явно путем добавления априорной информации I _m в расчеты. Таким образом, когда все, что известно о явлении, это то, что существует m известных возможных результатов до наблюдения каких-либо данных, только тогда применяется правило последовательности. Если правило последовательности применяется в задачах, где оно неточно описывает априорное состояние знаний, то оно может дать контринтуитивные результаты. Это происходит не потому, что правило последовательности дефектно, а потому, что оно эффективно отвечает на другой вопрос, основываясь на другой априорной информации.

В принципе (см. правило Кромвеля ), ни одна возможность не должна иметь вероятность (или псевдосчет), равную нулю, поскольку ничто в физическом мире не должно считаться строго невозможным (хотя это может быть так) — даже если это противоречит всем наблюдениям и текущим теориям. Действительно, правило Байеса абсолютно не учитывает наблюдение, которое ранее считалось имеющим нулевую вероятность — оно все равно объявляется невозможным. Однако приемлемым путем является рассмотрение только фиксированного набора возможностей, нужно просто помнить, что результаты обусловлены (или ограничены) рассматриваемым набором, а не некоторым «универсальным» набором. Фактически, Ларри Бретхорст показывает, что включение возможности «чего-то еще» в пространство гипотез не влияет на относительные вероятности другой гипотезы — оно просто перенормирует их, чтобы в сумме дать значение меньше 1. ^[8] Пока «что-то еще» не указано, функция правдоподобия, обусловленная этим «чем-то еще», является неопределенной, поскольку как определить ? Таким образом, обновление априорной вероятности для «чего-то другого» не может произойти, пока оно не будет определено более точно.${\displaystyle Pr({\text{data}}|{\text{something else}},I)}$

Однако иногда возникает вопрос, должны ли априорные знания влиять на относительные вероятности или также на общий вес априорных знаний по сравнению с фактическими наблюдениями. На этот вопрос нет однозначного ответа, поскольку он зависит от того, какие априорные знания рассматриваются. Фактически, альтернативное априорное состояние знаний может иметь вид «Я указал m потенциальных категорий, но я уверен, что только одна из них возможна до наблюдения данных. Однако я не знаю, какая именно это категория». Математический способ описания этого априорного знания — это распределение Дирихле со всеми параметрами, равными m ⁻¹ , которое затем дает псевдосчетчик 1 в знаменателе вместо m и добавляет псевдосчетчик m ⁻¹ к каждой категории. Это дает немного другую вероятность в двоичном случае .${\displaystyle {\frac {s+0.5}{n+1}}}$

Априорные вероятности стоит тратить значительные усилия на оценку только тогда, когда они, вероятно, окажут значительное влияние. Они могут быть важны, когда есть немного наблюдений — особенно когда их так мало, что было мало, если вообще было, наблюдений некоторых возможностей — например, редкого животного в данном регионе. Также важны, когда есть много наблюдений, когда считается, что ожидание должно быть сильно перевешено в сторону априорных оценок, несмотря на многие наблюдения об обратном, например, для рулетки в уважаемом казино. В последнем случае, по крайней мере, некоторые из псевдосчетчиков могут быть очень большими. Они не всегда малы, и поэтому вскоре перевешиваются фактическими наблюдениями, как часто предполагается. Однако, хотя это и последнее средство, для повседневных целей априорные знания обычно жизненно важны. Поэтому большинство решений должны быть в некоторой степени субъективными (в зависимости от аналитика и используемого анализа).

• Аддитивное сглаживание
• Оценка Кричевского–Трофимова
• Принцип безразличия