Частица в одномерной решетке

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены. Найти источники:  «Частица в одномерной решетке» – новости  · газеты  · книги  · ученый  · JSTOR ( декабрь 2013 г. ) ( Узнайте, как и когда удалять это сообщение )

В квантовой механике частица в одномерной решетке — это проблема, которая возникает в модели периодической кристаллической решетки . Потенциал обусловлен ионами в периодической структуре кристалла, создающими электромагнитное поле , поэтому электроны подвергаются регулярному потенциалу внутри решетки. Это обобщение модели свободных электронов , которая предполагает нулевой потенциал внутри решетки.

Когда речь идет о твердых материалах, речь идет в основном о кристаллах – периодических решетках. Здесь мы обсудим одномерную решетку положительных ионов. Если предположить, что расстояние между двумя ионами равно a , то потенциал в решетке будет выглядеть примерно так:

Математическое представление потенциала представляет собой периодическую функцию с периодом a . Согласно теореме Блоха ^[1] , волновое решение уравнения Шредингера , когда потенциал является периодическим, можно записать в виде:

$${\displaystyle \psi (x)=e^{ikx}u(x),}$$

где u ( x ) — периодическая функция , которая удовлетворяет u ( x + a ) = u ( x ) . Это фактор Блоха с показателем Флоке , который приводит к зонной структуре энергетического спектра уравнения Шредингера с периодическим потенциалом, таким как потенциал Кронига–Пенни или косинусная функция, как это было показано в 1928 году Стрэттом ^[2] . Решения могут быть получены с помощью функций Матье .${\displaystyle к}$

При приближении к краям решетки возникают проблемы с граничным условием. Поэтому мы можем представить ионную решетку в виде кольца, следуя граничным условиям Борна–фон Кармана . Если L — длина решетки, так что L ≫ a , то число ионов в решетке настолько велико, что при рассмотрении одного иона его окружение почти линейно, а волновая функция электрона неизменна. Так что теперь вместо двух граничных условий мы получаем одно круговое граничное условие:$${\displaystyle \psi (0)=\psi (L).}$$

Если N — число ионов в решетке, то имеем соотношение: aN = L. Замена в граничном условии и применение теоремы Блоха приведет к квантованию для k :$${\displaystyle \psi (0)=e^{ik\cdot 0}u(0)=e^{ikL}u(L)=\psi (L)}$$$${\displaystyle u(0)=e^{ikL}u(L)=e^{ikL}u(Na)\to e^{ikL}=1}$$$${\displaystyle \Rightarrow kL=2\pi n\to k={2\pi \over L}n\qquad \left(n=0,\pm 1,\dots ,\pm {\frac {N}{2}}\right).}$$

Модель Кронига–Пенни (названная в честь Ральфа Кронига и Уильяма Пенни ^[3] ) представляет собой простую идеализированную квантово-механическую систему, состоящую из бесконечного периодического массива прямоугольных потенциальных барьеров .

Потенциальная функция аппроксимируется прямоугольным потенциалом:

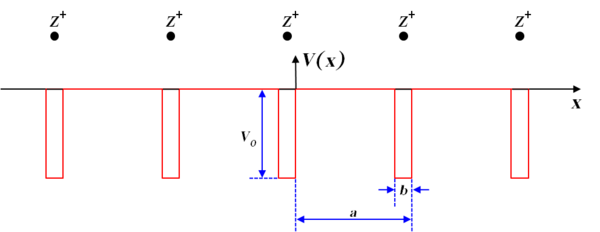
Используя теорему Блоха , нам нужно найти решение только для одного периода, убедиться, что оно непрерывно и гладко, а также убедиться, что функция u ( x ) также непрерывна и гладка.

Рассматривая один период потенциала:
У нас здесь есть две области. Мы решим для каждой независимо: Пусть E будет значением энергии выше ямы (E>0)

• Для :${\displaystyle 0<x<(a-b)}$$${\displaystyle {\begin{aligned}{\frac {-\hbar ^{2}}{2m}}\psi _{xx}&=E\psi \\\Rightarrow \psi &=Ae^{i\alpha x}+A'e^{-i\alpha x}&\left(\alpha ^{2}={2mE \over \hbar ^{2}}\right)\end{aligned}}}$$
• Для :${\displaystyle -b<x<0}$$${\displaystyle {\begin{aligned}{\frac {-\hbar ^{2}}{2m}}\psi _{xx}&=(E+V_{0})\psi \\\Rightarrow \psi &=Be^{i\beta x}+B'e^{-i\beta x}&\left(\beta ^{2}={2m(E+V_{0}) \over \hbar ^{2}}\right).\end{aligned}}}$$

Чтобы найти u ( x ) в каждой области, нам нужно манипулировать волновой функцией электрона:$${\displaystyle {\begin{aligned}\psi (0<x<a-b)&=Ae^{i\alpha x}+A'e^{-i\alpha x}=e^{ikx}\left(Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}\right)\\\Rightarrow u(0<x<a-b)&=Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}.\end{aligned}}}$$

И таким же образом:$${\displaystyle u(-b<x<0)=Be^{i(\beta -k)x}+B'e^{-i(\beta +k)x}.}$$

Для завершения решения нам необходимо убедиться, что функция вероятности является непрерывной и гладкой, то есть:$${\displaystyle \psi (0^{-})=\psi (0^{+})\qquad \psi '(0^{-})=\psi '(0^{+}).}$$

И что u ( x ) и u′ ( x ) являются периодическими:$${\displaystyle u(-b)=u(a-b)\qquad u'(-b)=u'(a-b).}$$

Эти условия дают следующую матрицу:$${\displaystyle {\begin{pmatrix}1&1&-1&-1\\\alpha &-\alpha &-\beta &\beta \\e^{i(\alpha -k)(a-b)}&e^{-i(\alpha +k)(a-b)}&-e^{-i(\beta -k)b}&-e^{i(\beta +k)b}\\(\alpha -k)e^{i(\alpha -k)(a-b)}&-(\alpha +k)e^{-i(\alpha +k)(a-b)}&-(\beta -k)e^{-i(\beta -k)b}&(\beta +k)e^{i(\beta +k)b}\end{pmatrix}}{\begin{pmatrix}A\\A'\\B\\B'\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\0\end{pmatrix}}.}$$

Чтобы получить нетривиальное решение, определитель матрицы должен быть равен 0. Это приводит нас к следующему выражению:$${\displaystyle \cos(ka)=\cos(\beta b)\cos[\alpha (a-b)]-{\alpha ^{2}+\beta ^{2} \over 2\alpha \beta }\sin(\beta b)\sin[\alpha (a-b)].}$$

Для дальнейшего упрощения выражения выполним следующие приближения:$${\displaystyle b\to 0;\quad V_{0}\to \infty ;\quad V_{0}b=\mathrm {constant} }$$$${\displaystyle \Rightarrow \beta ^{2}b=\mathrm {constant} ;\quad \alpha ^{2}b\to 0}$$$${\displaystyle \Rightarrow \beta b\to 0;\quad \sin(\beta b)\to \beta b;\quad \cos(\beta b)\to 1.}$$

Выражение теперь будет таким:$${\displaystyle \cos(ka)=\cos(\alpha a)+P{\frac {\sin(\alpha a)}{\alpha a}},\qquad P={\frac {mV_{0}ba}{\hbar ^{2}}}.}$$

Для значений энергии внутри ямы ( E  < 0) получаем: при и .$${\displaystyle \cos(ka)=\cos(\beta b)\cosh[\alpha (a-b)]-{\beta ^{2}-\alpha ^{2} \over 2\alpha \beta }\sin(\beta b)\sinh[\alpha (a-b)],}$$${\displaystyle \alpha ^{2}={2m|E| \over \hbar ^{2}}}$${\displaystyle \beta ^{2}={\frac {2m(V_{0}-|E|)}{\hbar ^{2}}}}$

Следуя тем же приближениям, что и выше ( ), приходим к той же формуле для P , что и в предыдущем случае .${\displaystyle b\to 0;\,V_{0}\to \infty ;\,V_{0}b=\mathrm {constant} }$$${\displaystyle \cos(ka)=\cosh(\alpha a)+P{\frac {\sinh(\alpha a)}{\alpha a}}}$$${\displaystyle \left(P={\frac {mV_{0}ba}{\hbar ^{2}}}\right)}$

В предыдущем параграфе единственными переменными, не определяемыми параметрами физической системы, являются энергия E и импульс кристалла k . Выбрав значение для E , можно вычислить правую часть, а затем вычислить k , взяв от обеих сторон. Таким образом, выражение приводит к дисперсионному соотношению .${\displaystyle \arccos }$

Правая часть последнего выражения выше иногда может быть больше 1 или меньше –1, и в этом случае нет значения k , которое может сделать уравнение верным. Поскольку , это означает, что существуют определенные значения E , для которых нет собственных функций уравнения Шредингера. Эти значения составляют запрещенную зону .${\displaystyle \alpha a\propto {\sqrt {E}}}$

Таким образом, модель Кронига–Пенни является одним из простейших периодических потенциалов, демонстрирующих наличие запрещенной зоны.

Приводится альтернативное решение ^[4] аналогичной проблемы. Здесь мы имеем дельта- периодический потенциал:$${\displaystyle V(x)=A\cdot \sum _{n=-\infty }^{\infty }\delta (x-na).}$$

A — некоторая константа, а a — константа решетки (расстояние между каждым узлом). Поскольку этот потенциал является периодическим, мы могли бы разложить его в ряд Фурье: где$${\displaystyle V(x)=\sum _{K}{\tilde {V}}(K)\cdot e^{iKx},}$$$${\displaystyle {\tilde {V}}(K)={\frac {1}{a}}\int _{-a/2}^{a/2}dx\,V(x)\,e^{-iKx}={\frac {1}{a}}\int _{-a/2}^{a/2}dx\sum _{n=-\infty }^{\infty }A\cdot \delta (x-na)\,e^{-iKx}={\frac {A}{a}}.}$$

Волновая функция, используя теорему Блоха, равна, где — периодическая в решетке функция, а это значит, что мы можем разложить ее и в ряд Фурье:${\displaystyle \psi _{k}(x)=e^{ikx}u_{k}(x)}$${\displaystyle u_{k}(x)}$$${\displaystyle u_{k}(x)=\sum _{K}{\tilde {u}}_{k}(K)e^{iKx}.}$$

Таким образом, волновая функция имеет вид:$${\displaystyle \psi _{k}(x)=\sum _{K}{\tilde {u}}_{k}(K)\,e^{i(k+K)x}.}$$

Подставляя это в уравнение Шредингера, получаем: или, скорее:$${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+\sum _{K'}{\tilde {V}}(K-K')\,{\tilde {u}}_{k}(K')=0}$$$${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+{\frac {A}{a}}\sum _{K'}{\tilde {u}}_{k}(K')=0}$$

Теперь мы осознаем, что:$${\displaystyle u_{k}(0)=\sum _{K'}{\tilde {u}}_{k}(K')}$$

Подставим это в уравнение Шредингера:$${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+{\frac {A}{a}}u_{k}(0)=0}$$

Решая это, получаем:${\displaystyle {\tilde {u}}_{k}(K)}$$${\displaystyle {\tilde {u}}_{k}(K)={\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}f(k)}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}={\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$$

Просуммируем это последнее уравнение по всем значениям K и получим:$${\displaystyle \sum _{K}{\tilde {u}}_{k}(K)=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$$

Или:$${\displaystyle u_{k}(0)=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$$

Удобно, сокращаем и получаем:${\displaystyle u_{k}(0)}$$${\displaystyle 1=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}}$$

Или:$${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{K}{\frac {1}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}}$$

Чтобы сэкономить время на ненужную запись, мы определяем новую переменную: и в итоге наше выражение выглядит так:$${\displaystyle \alpha ^{2}:={\frac {2mE_{k}}{\hbar ^{2}}}}$$$${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{K}{\frac {1}{\alpha ^{2}-(k+K)^{2}}}}$$

Теперь K — вектор обратной решетки, что означает, что сумма по K на самом деле является суммой по целым кратным :${\displaystyle {\frac {2\pi }{a}}}$$${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{n=-\infty }^{\infty }{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}}$$

Мы можем немного изменить это выражение, чтобы сделать его более наглядным (используем разложение на простые дроби ):$${\displaystyle {\begin{aligned}{\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}&=\sum _{n=-\infty }^{\infty }{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}\\&=-{\frac {1}{2\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{(k+{\frac {2\pi n}{a}})-\alpha }}-{\frac {1}{(k+{\frac {2\pi n}{a}})+\alpha }}\right]\\&=-{\frac {a}{4\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\\&=-{\frac {a}{4\alpha }}\left[\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\end{aligned}}}$$

Если мы используем хорошее тождество суммы функции котангенса (уравнение 18), которое гласит: и подставим его в наше выражение, то получим:$${\displaystyle \cot(x)=\sum _{n=-\infty }^{\infty }{\frac {1}{2\pi n+2x}}-{\frac {1}{2\pi n-2x}}}$$$${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=-{\frac {a}{4\alpha }}\left[\cot \left({\tfrac {ka}{2}}-{\tfrac {\alpha a}{2}}\right)-\cot \left({\tfrac {ka}{2}}+{\tfrac {\alpha a}{2}}\right)\right]}$$

Мы используем сумму cot , а затем произведение sin (которое является частью формулы для суммы cot ), чтобы получить:$${\displaystyle \cos(ka)=\cos(\alpha a)+{\frac {mA}{\hbar ^{2}\alpha }}\sin(\alpha a)}$$

Это уравнение показывает связь между энергией (через α ) и волновым вектором k , и, как вы можете видеть, поскольку левая часть уравнения может изменяться только от −1 до 1 , то существуют некоторые ограничения на значения, которые может принимать α (и, следовательно, энергия), то есть в некоторых диапазонах значений энергии нет решения согласно этому уравнению, и, таким образом, система не будет иметь этих энергий: энергетические щели. Это так называемые запрещенные зоны, которые, как можно показать, существуют в любой форме периодического потенциала (не только в дельта- или квадратных барьерах).

Для другого и подробного расчета формулы щели (т. е. щели между полосами) и расщепления уровней собственных значений одномерного уравнения Шредингера см. Мюллер-Кирстен. ^[5] Соответствующие результаты для косинусного потенциала (уравнение Матье) также подробно приведены в этой ссылке.

В некоторых случаях уравнение Шредингера можно решить аналитически на одномерной решетке конечной длины ^{[6] [7]} с использованием теории периодических дифференциальных уравнений. ^[8] Предполагается, что длина решетки равна , где — период потенциала, а число периодов — положительное целое число. Два конца решетки находятся в и , где определяет точку окончания. Волновая функция обращается в нуль вне интервала .${\displaystyle L=Na}$${\displaystyle a}$${\displaystyle N}$${\displaystyle \tau }$${\displaystyle L+\tau }$${\displaystyle \tau }$${\displaystyle [\tau ,L+\tau ]}$

Собственные состояния конечной системы можно найти в терминах блоховских состояний бесконечной системы с тем же периодическим потенциалом. Если между двумя последовательными энергетическими зонами бесконечной системы имеется запрещенная зона, то в конечной решетке существует резкое различие между двумя типами состояний. Для каждой энергетической зоны бесконечной системы существуют объемные состояния, энергии которых зависят от длины , но не от окончания . Эти состояния представляют собой стоячие волны, построенные как суперпозиция двух блоховских состояний с импульсами и , где выбрано так, чтобы волновая функция обращалась в нуль на границах. Энергии этих состояний соответствуют энергетическим зонам бесконечной системы. ^[6]${\displaystyle N-1}$${\displaystyle N}$${\displaystyle \tau }$${\displaystyle k}$${\displaystyle -k}$${\displaystyle k}$

Для каждой запрещенной зоны существует одно дополнительное состояние. Энергии этих состояний зависят от точки окончания , но не от длины . ^[6] Энергия такого состояния может лежать либо на краю зоны, либо внутри запрещенной зоны. Если энергия находится внутри запрещенной зоны, состояние является поверхностным состоянием, локализованным на одном конце решетки, но если энергия находится на краю зоны, состояние делокализовано по всей решетке.${\displaystyle \tau }$${\displaystyle N}$

• Приближение пустой решетки
• Модель почти свободных электронов
• Кристаллическая структура

• «Модель Кронига–Пенни» Майкла Краучера, интерактивный расчет 1d периодической потенциальной зонной структуры с использованием Mathematica , из проекта Wolfram Demonstrations Project .