Диаграммы углового момента (квантовая механика)
| Часть серии статей о |
| Квантовая механика |
|---|
В квантовой механике и ее приложениях к квантовым многочастичным системам , в частности, в квантовой химии , диаграммы углового момента или, точнее, с математической точки зрения, графики углового момента являются диаграммным методом представления квантовых состояний углового момента квантовой системы, позволяющим выполнять вычисления символически. Более конкретно, стрелки кодируют состояния углового момента в скобочной нотации и включают абстрактную природу состояния, такую как тензорные произведения и правила преобразования.
Обозначение соответствует идее графической нотации Пенроуза и диаграмм Фейнмана . Диаграммы состоят из стрелок и вершин с квантовыми числами в качестве меток, отсюда и альтернативный термин « графики ». Смысл каждой стрелки связан с эрмитовым сопряжением , которое примерно соответствует обращению во времени состояний углового момента (ср. уравнение Шредингера ). Диаграммная нотация сама по себе является довольно большой темой с рядом специализированных особенностей — эта статья знакомит с самыми основами.
Они были разработаны главным образом Адольфасом Юцисом (иногда его переводят как Юцис) в двадцатом веке.
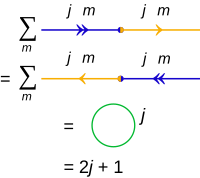
Эквивалентность между обозначениями Дирака и диаграммами Юсиса
Состояния углового момента
Вектор квантового состояния отдельной частицы с полным квантовым числом углового момента j и полным магнитным квантовым числом m = j , j − 1, ..., − j + 1, − j , обозначается как кет | j , m ⟩ . На диаграмме это однонаправленная стрелка.
Симметрично, соответствующий бюстгальтер — ⟨ j , m | . В виде диаграммы это двунаправленная стрелка, указывающая в противоположном направлении кету.
В каждом случае;
- Квантовые числа j , m часто указываются рядом со стрелками, чтобы обозначить определенное состояние углового момента,
- Наконечники стрел почти всегда располагаются посередине линии, а не на конце,
- Между эквивалентными диаграммами ставятся знаки равенства «=», точно так же, как для нескольких алгебраических выражений, равных друг другу.
Самые простые схемы предназначены для кетов и бюстгальтеров:
Стрелки направлены к вершинам или от вершин, состояние преобразуется в соответствии с:
- стандартное представление обозначается ориентированной линией, выходящей из вершины,
- Контрастное представление изображается как линия, входящая в вершину.
Как правило, стрелки следуют друг за другом в одном и том же смысле. В представлении contrastandard используется оператор обращения времени , обозначенный здесь как T. Он унитарен, что означает, что эрмитово сопряжение T † равно обратному оператору T −1 , то есть T † = T −1 . Его действие на оператор положения оставляет его инвариантным:
но оператор линейного импульса становится отрицательным:
и оператор спина становится отрицательным:
Поскольку оператор орбитального момента импульса равен L = x × p , он также должен стать отрицательным:
и поэтому оператор полного момента импульса J = L + S становится отрицательным:
Действуя на собственное состояние углового момента | j , m ⟩ , можно показать, что: [1]
Диаграммы, обращенные во времени, для кетов и бюстгальтеров:
Важно правильно расположить вершину, так как операторы прямого и обратного времени могут перепутаться.
Внутренний продукт
Скалярное произведение двух состояний | j 1 , m 1 ⟩ и | j 2 , m 2 ⟩ равно:
и диаграммы:
Для суммирования по внутреннему произведению, также известному в этом контексте как свертка (ср. тензорная контракция ):
принято обозначать результат в виде замкнутого круга, помеченного только буквой j , а не m :
Внешние продукты
Внешнее произведение двух состояний | j 1 , m 1 ⟩ и | j 2 , m 2 ⟩ является оператором:
и диаграммы:
Для суммирования по внешнему произведению, также известному в этом контексте как свертывание (ср. тензорное свертывание ):
где был использован результат для T | j , m ⟩ и тот факт, что m принимает набор значений, приведенных выше. Нет никакой разницы между состояниями прямого и обратного времени для сокращения внешнего продукта, поэтому здесь они разделяют одну и ту же диаграмму, представленную как одна линия без направления, снова помеченная только j , а не m :

Тензорные продукты
Тензорное произведение ⊗ n состояний | j 1 , m 1 ⟩ , | j 2 , m 2 ⟩ , ... | j n , m n ⟩ записывается как
а в виде диаграммы каждое отдельное состояние покидает или входит в общую вершину, создавая «веер» стрелок — n линий, прикрепленных к одной вершине.
Вершины в тензорных произведениях имеют знаки (иногда называемые «узловыми знаками»), указывающие порядок состояний, умноженных на тензор:
- знак минус (−) указывает на порядок по часовой стрелке , и
- знак плюс (+) для против часовой стрелки , .
Знаки, конечно, не требуются только для одного состояния, схематически одна стрелка в вершине. Иногда включаются изогнутые стрелки со знаками, чтобы явно показать смысл тензорного умножения, но обычно показывается только знак без стрелок.
Для внутреннего произведения двух тензорных произведений имеем:
существует n- ное количество стрелок внутреннего произведения:
Примеры и приложения
- Диаграммы хорошо подходят для коэффициентов Клебша–Гордана .
- Расчеты с реальными квантовыми системами, такими как многоэлектронные атомы и молекулярные системы.
Смотрите также
Ссылки
- Юцис, Адольфас П.; Левинсон, И.Б.; Ванагас, В.В. (1962). Математический аппарат теории углового момента. Перевод А. Сена; Р.Н. Сена. Израильская программа научных переводов.
- Вормер и Палдус (2006) [1] дают подробное руководство по диаграммам углового момента.
- I. Lindgren; J. Morrison (1986). Atomic Many-Body Theory. Chemical Physics. Vol. 13 (2nd ed.). Springer-Verlag. ISBN 978-3-540-16649-8.
Дальнейшее чтение
- GWF Drake (2006). Springer Handbook of Atomic, Molecular, and Optical Physics (2-е изд.). Springer. стр. 60. ISBN 978-0-387-26308-3.
- U. Kaldor; S. Wilson (2003). Теоретическая химия и физика тяжелых и сверхтяжелых элементов. Progress in Theoretical Chemistry and Physics. Vol. 11. Springer. стр. 183. ISBN 978-1-4020-1371-3.
- Э.Дж. Брендас; П.О. Лёвдин; Э. Брендас; Е. С. Крячко (2004). Фундаментальный мир квантовой химии: дань памяти Пер-Олову Лёвдину. Том. 3. Спрингер. п. 385. ИСБН 978-1-4020-2583-9.
- P. Schwerdtfeger (2004). Релятивистская электронная структурная теория: Часть 2. Приложения. Теоретическая и вычислительная химия. Т. 14. Elsevier. С. 97. ISBN 978-0-08-054047-4.
- M. Barysz; Y. Ishikawa (2010). Релятивистские методы для химиков. Проблемы и достижения в вычислительной химии и физике. Т. 10. Springer. С. 311. ISBN 978-1-4020-9975-5.
- GHF Diercksen; S. Wilson (1983). Методы вычислительной молекулярной физики. NATO Science Series C. Vol. 113. Springer. ISBN 978-90-277-1638-5.
- Зенонас Рудзикас (2007). "8". Теоретическая атомная спектроскопия . Кембриджские монографии по атомной, молекулярной и химической физике. Том 7. Чикагский университет: Cambridge University Press. ISBN 978-0-521-02622-2.
- «Летувос Физику Драугия» (2004). Журнал «Летувос физикос». Том. 44. Чикагский университет: Драугия.
- PET Jorgensen (1987). Операторы и теория представлений: канонические модели для алгебр операторов, возникающих в квантовой механике. Чикагский университет: Elsevier. ISBN 978-0-08-087258-2.
- P. Cvitanović (2008). Теория групп — следы птиц, ложь и исключительные группы. Принстон, Нью-Джерси: Princeton Univ. Press. ISBN 978-0-691-11836-9.
Примечания
- ^ ab PES Wormer; J. Paldus (2006). "Диаграммы углового момента". Advances in Quantum Chemistry . 51. Elsevier: 59– 124. Bibcode : 2006AdQC...51...59W. doi : 10.1016/S0065-3276(06)51002-0. ISBN 9780120348510. ISSN 0065-3276.Эти авторы используют тета-вариант ϑ для оператора обращения времени, здесь мы используем T.