Термодинамическая бета

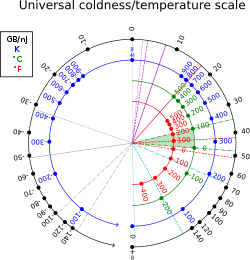
В статистической термодинамике термодинамическая бета , также известная как холодность , ^[1] является обратной величиной термодинамической температуры системы: (где T — температура, а k _B — постоянная Больцмана ). ^[2]$${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$$

Термодинамическая бета имеет единицы, обратные единицам энергии (в единицах СИ , обратные джоули , ). В нетепловых единицах ее также можно измерять в байтах на джоуль или, что более удобно, в гигабайтах на наноджоуль; ^[3] 1 К ⁻¹ эквивалентен примерно 13 062 гигабайтам на наноджоуль; при комнатной температуре: T = 300 К, β ≈${\displaystyle [\beta ]={\textrm {J}}^{-1}}$44 ГБ/нДж ≈39  эВ ⁻¹ ≈2,4 × 1020  Дж ⁻¹ . Коэффициент преобразования составляет 1 ГБ/нДж = ^Дж − ¹ .${\displaystyle 8\ln 2\times 10^{18}}$

Термодинамическая бета по сути является связью между теорией информации и статистической механикой интерпретации физической системы через ее энтропию и термодинамику , связанную с ее энергией . Она выражает реакцию энтропии на увеличение энергии. Если к системе добавляется небольшое количество энергии, то β описывает количество, которое система будет рандомизировать.

Используя статистическое определение температуры как функции энтропии, функцию холода можно рассчитать в микроканоническом ансамбле по формуле

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(т.е. частная производная энтропии S по энергии E при постоянном объеме V и числе частиц N ).

Хотя по концептуальному содержанию β полностью эквивалентна температуре, ее обычно считают более фундаментальной величиной, чем температуру, из-за явления отрицательной температуры , при котором β непрерывна при пересечении нуля, тогда как T имеет сингулярность. ^[4]

Кроме того, β имеет преимущество в том, что его легче понять причинно-следственно: если к системе добавляется небольшое количество тепла, β представляет собой увеличение энтропии, деленное на увеличение тепла. Температуру трудно интерпретировать в том же смысле, поскольку невозможно «добавить энтропию» к системе, кроме как косвенно, изменяя другие величины, такие как температура, объем или число частиц.

Со статистической точки зрения β — числовая величина, связывающая две макроскопические системы в равновесии. Точная формулировка такова. Рассмотрим две системы, 1 и 2, находящиеся в тепловом контакте, с соответствующими энергиями E ₁ и E ₂ . Мы предполагаем, что E ₁ + E ₂ = некоторая константа E . Число микросостояний каждой системы будет обозначаться как Ω ₁ и Ω ₂ . При наших предположениях Ω _i зависит только от E _i . Мы также предполагаем, что любое микросостояние системы 1, согласующееся с E _{1 ,} может сосуществовать с любым микросостоянием системы 2, согласующимся с E ₂ . Таким образом, число микросостояний для объединенной системы равно

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}( E-E_{1}).\,}$

Мы выведем β из фундаментального предположения статистической механики :

Когда объединенная система достигает равновесия, число Ω максимизируется.

(Другими словами, система естественным образом стремится к максимальному числу микросостояний.) Поэтому в состоянии равновесия

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Но E ₁ + E ₂ = E подразумевает

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Так

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

то есть

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{at equilibrium.}}}$

Вышеприведенное соотношение мотивирует определение β :

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Когда две системы находятся в равновесии, они имеют одинаковую термодинамическую температуру T. Таким образом, интуитивно можно было бы ожидать, что β (определенная через микросостояния) каким-то образом связана с T. Эта связь обеспечивается фундаментальным предположением Больцмана, записанным как

${\displaystyle S=k_{\rm {B}}\ln \Omega ,}$

где k _B — постоянная Больцмана , S — классическая термодинамическая энтропия, а Ω — число микросостояний. Итак

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Подстановка в определение β из статистического определения выше дает

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Сравнение с термодинамической формулой

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

у нас есть

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

где называется фундаментальной температурой системы и имеет единицы измерения энергии.${\displaystyle \tau }$

This section's factual accuracy is disputed. Relevant discussion may be found on the talk page. Please help to ensure that disputed statements are reliably sourced. (September 2024) (Learn how and when to remove this message)

Термодинамическая бета была первоначально введена в 1971 году (как Kältefunktion «функция холода») Инго Мюллером  [de] , одним из сторонников школы рациональной термодинамики , ^{[5] [6]} на основе более ранних предложений о функции «обратной температуры». ^{[1] [7] [ необходим непервичный источник ]}

• Распределение Больцмана
• Канонический ансамбль
• модель Изинга