Пересечение


В математике пересечение двух или более объектов — это другой объект, состоящий из всего, что содержится во всех объектах одновременно. Например, в евклидовой геометрии , когда две прямые на плоскости не параллельны, их пересечение — это точка , в которой они встречаются. В более общем смысле, в теории множеств пересечение множеств определяется как множество элементов , которые принадлежат всем им. В отличие от евклидова определения, это не предполагает, что рассматриваемые объекты лежат в общем пространстве .
Пересечение является одним из основных понятий геометрии . Пересечение может иметь различные геометрические формы , но точка является наиболее распространенной в плоской геометрии . Геометрия инцидентности определяет пересечение (обычно плоских поверхностей ) как объект меньшей размерности , который инцидентен каждому из исходных объектов. При таком подходе пересечение иногда может быть неопределенным, например, для параллельных линий . В обоих случаях понятие пересечения опирается на логическое соединение . Алгебраическая геометрия определяет пересечения по-своему с помощью теории пересечений .
Уникальность
Может быть более одного примитивного объекта, например, точек (на фото выше), которые образуют пересечение. Пересечение можно рассматривать как совокупность всех общих объектов (т. е. операция пересечения приводит к множеству , возможно пустому), или как несколько объектов пересечения ( возможно, нулю ).
В теории множеств

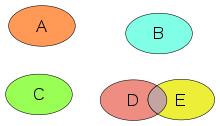
Пересечение двух множеств A и B — это множество элементов, которые находятся как в A, так и в B. Формально,
- . [1]
Например, если и , то . Более сложный пример (с участием бесконечных множеств):
В качестве другого примера, число 5 не содержится в пересечении множества простых чисел {2, 3, 5, 7, 11, …} и множества четных чисел {2, 4, 6, 8, 10, …} , потому что хотя 5 и является простым числом, оно не является четным. Фактически, число 2 является единственным числом в пересечении этих двух множеств. В этом случае пересечение имеет математический смысл: число 2 является единственным четным простым числом.
В геометрии

В геометрии пересечение — это точка, линия или кривая, общие для двух или более объектов (таких как линии, кривые, плоскости и поверхности). Простейшим случаем в евклидовой геометрии является пересечение прямой между двумя различными прямыми , которое либо является одной точкой (иногда называемой вершиной ), либо не существует (если прямые параллельны ). Другие типы геометрического пересечения включают:
- Пересечение прямой и плоскости
- Пересечение линии и сферы
- Пересечение многогранника с прямой
- Пересечение отрезков линий
- Кривая пересечения
Обозначение
Пересечение обозначается как U+2229 ∩ INTERSECTION из Unicode Mathematical Operators .
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion with: history of the symbol. You can help by adding to it. (January 2014) |
Символ U+2229 ∩ INTERSECTION впервые был использован Германом Грассманом в Die Ausdehnungslehre von 1844 как общий операционный символ, не специализированный для пересечения. Оттуда он использовался Джузеппе Пеано (1858–1932) для пересечения в 1888 году в Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann . [2] [3]
Пеано также создал большие символы для общего пересечения и объединения более чем двух классов в своей книге 1908 года «Mathematico Formulario» . [4] [5]
Смотрите также
- Конструктивная сплошная геометрия , Булево пересечение — один из способов объединения 2D/3D фигур.
- Пространственно расширенная модель 9-пересечений
- Знакомьтесь (теория решеток)
- Пересечение (теория множеств)
- Объединение (теория множеств)
Ссылки
- ^ Верещагин, Николай Константинович; Шен, Александр (2002-01-01). Базовая теория множеств. Американское математическое общество. ISBN 9780821827314.
- ^ Пеано, Джузеппе (1 января 1888 г.). Calcolo Geometry Secondo l'Ausdehnungslehre di H. Grassmann: Preceduto dalleoperazioni della Logica deduttiva (на итальянском языке). Турин: Фрателли Бокка .
- ^ Каджори, Флориан (2007-01-01). История математических обозначений. Турин: Cosimo, Inc. ISBN 9781602067141.
- ^ Пеано, Джузеппе (1 января 1908 г.). Formulario mathematico, том V (на итальянском языке). Турин: Edizione cremonese (факсимиле-перепечатка в Риме, 1960). п. 82. ОСЛК 23485397.
- ^ Раннее использование символов теории множеств и логики
Внешние ссылки
- Вайсштейн, Эрик В. «Пересечение». MathWorld .








