Теория информационного поля

Теория информационного поля (IFT) — это байесовская статистическая теория поля, относящаяся к реконструкции сигналов , космографии и другим смежным областям. [1] [2] IFT суммирует имеющуюся информацию о физическом поле с помощью байесовских вероятностей . Она использует вычислительные методы, разработанные для квантовой теории поля и статистической теории поля, для обработки бесконечного числа степеней свободы поля и для вывода алгоритмов для расчета значений ожиданий поля . Например, апостериорное ожидание поля, созданного известным гауссовым процессом и измеренного линейным устройством с известной статистикой гауссовского шума , задается обобщенным фильтром Винера, примененным к измеренным данным. IFT расширяет такую ​​известную формулу фильтра на ситуации с нелинейной физикой , нелинейными устройствами , негауссовой статистикой поля или шума, зависимостью статистики шума от значений поля и частично неизвестными параметрами измерения. Для этого она использует диаграммы Фейнмана , уравнения потока перенормировки и другие методы из математической физики . [3]

Мотивация

Поля играют важную роль в науке, технике и экономике. Они описывают пространственные изменения величины, например температуры воздуха, как функцию положения. Знание конфигурации поля может иметь большое значение. Однако измерения полей никогда не могут с уверенностью предоставить точную конфигурацию поля. Физические поля имеют бесконечное число степеней свободы, но данные, генерируемые любым измерительным устройством, всегда конечны, обеспечивая только конечное число ограничений для поля. Таким образом, однозначный вывод такого поля только из данных измерений невозможен, и только вероятностный вывод остается средством для утверждения о поле. К счастью, физические поля демонстрируют корреляции и часто следуют известным физическим законам. Такая информация лучше всего объединяется с выводом поля, чтобы преодолеть несоответствие степеней свободы поля точкам измерения. Чтобы справиться с этим, необходима информационная теория для полей, и это то, чем является теория информационного поля.

Концепции

Байесовский вывод

с ( х ) {\displaystyle s(x)} это значение поля в определенном месте в пространстве . Априорные знания о неизвестном поле сигнала закодированы в распределении вероятностей . Данные предоставляют дополнительную информацию о с помощью вероятности , которая включается в апостериорную вероятность согласно теореме Байеса . х ∈ Ω {\displaystyle x\in \Омега} Ω {\displaystyle \Омега} с {\displaystyle с} П ( с ) {\displaystyle {\mathcal {P}}(s)} г {\displaystyle д} с {\displaystyle с} П ( г | с ) {\displaystyle {\mathcal {P}}(d|s)} П ( с | г ) = П ( г | с ) П ( с ) П ( г ) {\displaystyle {\mathcal {P}}(s|d)={\frac {{\mathcal {P}}(d|s)\,{\mathcal {P}}(s)}{{\mathcal {P}}(d)}}}

ИнформацияГамильтониан

В IFT теорема Байеса обычно переписывается на языке статистической теории поля, при этом информационный гамильтониан определяется как отрицательный логарифм совместной вероятности данных и сигнала, а функция распределения имеет вид Эта переформулировка теоремы Байеса позволяет использовать методы математической физики, разработанные для обработки статистических теорий поля и квантовых теорий поля . П ( с | г ) = П ( г , с ) П ( г ) ≡ е − ЧАС ( г , с ) З ( г ) , {\displaystyle {\mathcal {P}}(s|d)={\frac {{\mathcal {P}}(d,s)}{{\mathcal {P}}(d)}}\equiv {\frac {e^{-{\mathcal {H}}(d,s)}}{{\mathcal {Z}}(d)}},} ЧАС ( г , с ) ≡ − вн ⁡ П ( г , с ) = − вн ⁡ П ( г | с ) − вн ⁡ П ( с ) ≡ ЧАС ( г | с ) + ЧАС ( с ) , {\displaystyle {\mathcal {H}}(d,s)\equiv -\ln {\mathcal {P}}(d,s)=-\ln {\mathcal {P}}(d|s)-\ln {\mathcal {P}}(s)\equiv {\mathcal {H}}(d|s)+{\mathcal {H}}(s),} З ( г ) ≡ П ( г ) = ∫ Д с П ( г , с ) . {\displaystyle {\mathcal {Z}}(d)\equiv {\mathcal {P}}(d)=\int {\mathcal {D}}s\,{\mathcal {P}}(d,s).}

Поля

Поскольку поля имеют бесконечное число степеней свободы, определение вероятностей над пространствами конфигураций полей имеет тонкости. Определение физических полей как элементов функциональных пространств создает проблему, заключающуюся в том, что над последними не определена мера Лебега , и, следовательно, плотности вероятностей там не могут быть определены. Однако физические поля имеют гораздо большую регулярность, чем большинство элементов функциональных пространств, поскольку они непрерывны и гладки в большинстве своих местоположений. Поэтому для обработки бесконечного числа степеней свободы поля можно использовать менее общие, но достаточно гибкие конструкции.

Прагматичный подход заключается в том, чтобы считать поле дискретизированным в терминах пикселей. Каждый пиксель несет одно значение поля, которое предполагается постоянным в пределах объема пикселя. Все утверждения о непрерывном поле затем должны быть приведены к его пиксельному представлению. Таким образом, мы имеем дело с конечномерными полевыми пространствами, по которым плотности вероятности хорошо определяются.

Для того чтобы это описание было правильной теорией поля, необходимо также, чтобы разрешение пикселей всегда можно было уточнить, а ожидаемые значения дискретизированного поля сходились к конечным значениям: Δ x {\displaystyle \Delta x} s Δ x {\displaystyle s_{\Delta x}} ⟨ f ( s ) ⟩ ( s | d ) ≡ lim Δ x → 0 ∫ d s Δ x f ( s Δ x ) P ( s Δ x ) . {\displaystyle \langle f(s)\rangle _{(s|d)}\equiv \lim _{\Delta x\rightarrow 0}\int ds_{\Delta x}f(s_{\Delta x})\,{\mathcal {P}}(s_{\Delta x}).}

Интегралы по траектории

Если этот предел существует, можно говорить об интеграле пространства конфигурации поля или интеграле по траектории, независимо от разрешения, с которым он может быть оценен численно. ⟨ f ( s ) ⟩ ( s | d ) ≡ ∫ D s f ( s ) P ( s ) . {\displaystyle \langle f(s)\rangle _{(s|d)}\equiv \int {\mathcal {D}}s\,f(s)\,{\mathcal {P}}(s).}

Гауссово априорное распределение

Простейшим априорным распределением для поля является распределение вероятностей Гаусса с нулевым средним . Определитель в знаменателе может быть плохо определен в пределе континуума , однако все, что необходимо для согласованности IFT, — это то, что этот определитель можно оценить для любого представления поля с конечным разрешением с помощью и что это позволяет вычислять сходящиеся значения ожиданий. P ( s ) = G ( s , S ) ≡ 1 | 2 π S | e − 1 2 s † S − 1 s . {\displaystyle {\mathcal {P}}(s)={\mathcal {G}}(s,S)\equiv {\frac {1}{|2\pi S|}}e^{-{\frac {1}{2}}\,s^{\dagger }S^{-1}\,s}.} Δ x → 0 {\displaystyle \Delta x\rightarrow 0} Δ x > 0 {\displaystyle \Delta x>0}

Гауссовское распределение вероятностей требует спецификации двухточечной корреляционной функции поля с коэффициентами и скалярным произведением для непрерывных полей, относительно которых строится обратная ковариация поля сигнала, т.е. S ≡ ⟨ s s † ⟩ ( s ) {\displaystyle S\equiv \langle s\,s^{\dagger }\rangle _{(s)}} S x y ≡ ⟨ s ( x ) s ( y ) ¯ ⟩ ( s ) {\displaystyle S_{xy}\equiv \langle s(x)\,{\overline {s(y)}}\rangle _{(s)}} a † b ≡ ∫ Ω d x a ( x ) ¯ b ( x ) , {\displaystyle a^{\dagger }b\equiv \int _{\Omega }dx\,{\overline {a(x)}}\,b(x),} S − 1 {\displaystyle S^{-1}} ( S − 1 S ) x y ≡ ∫ Ω d z ( S − 1 ) x z S z y = 1 x y ≡ δ ( x − y ) . {\displaystyle (S^{-1}S)_{xy}\equiv \int _{\Omega }dz\,(S^{-1})_{xz}S_{zy}=\mathbb {1} _{xy}\equiv \delta (x-y).}

Соответствующий гамильтониан априорной информации имеет вид H ( s ) = − ln ⁡ G ( s , S ) = 1 2 s † S − 1 s + 1 2 ln ⁡ | 2 π S | . {\displaystyle {\mathcal {H}}(s)=-\ln {\mathcal {G}}(s,S)={\frac {1}{2}}\,s^{\dagger }S^{-1}\,s+{\frac {1}{2}}\,\ln |2\pi S|.}

Уравнение измерения

Данные измерений были получены с вероятностью . В случае, если прибор был линейным, можно задать уравнение измерения в форме , в которой есть отклик прибора, который описывает, как данные в среднем реагируют на сигнал, а есть шум, просто разница между данными и линейным откликом сигнала . Отклик переводит бесконечномерный вектор сигнала в конечномерное пространство данных. В компонентах это читается как d {\displaystyle d} P ( d | s ) {\displaystyle {\mathcal {P}}(d|s)} d = R s + n {\displaystyle d=R\,s+n} R {\displaystyle R} n {\displaystyle n} d {\displaystyle d} R s {\displaystyle R\,s} d i = ∫ Ω d x R i x s x + n i , {\displaystyle d_{i}=\int _{\Omega }dx\,R_{ix}\,s_{x}+n_{i},}

где также была введена векторная компонентная нотация для векторов сигналов и данных.

Если шум следует независимой от сигнала гауссовой статистике с нулевым средним и ковариацией , то правдоподобие также является гауссовым, а гамильтониан информации о правдоподобии равен Линейное измерение гауссовского сигнала, подверженного гауссовскому и независимому от сигнала шуму, приводит к свободному IFT. N {\displaystyle N} P ( n | s ) = G ( n , N ) , {\displaystyle {\mathcal {P}}(n|s)={\mathcal {G}}(n,N),} P ( d | s ) = G ( d − R s , N ) , {\displaystyle {\mathcal {P}}(d|s)={\mathcal {G}}(d-R\,s,N),} H ( d | s ) = − ln ⁡ G ( d − R s , N ) = 1 2 ( d − R s ) † N − 1 ( d − R s ) + 1 2 ln ⁡ | 2 π N | . {\displaystyle {\mathcal {H}}(d|s)=-\ln {\mathcal {G}}(d-R\,s,N)={\frac {1}{2}}\,(d-R\,s)^{\dagger }N^{-1}\,(d-R\,s)+{\frac {1}{2}}\,\ln |2\pi N|.}

Свободная теория

Свободный гамильтониан

Совместный информационный гамильтониан гауссовского сценария, описанного выше, имеет вид , где обозначает равенство с точностью до несущественных констант, что в данном случае означает выражения, не зависящие от . Из этого ясно, что апостериорная функция должна быть гауссовой со средним значением и дисперсией , где равенство между правой и левой частями выполняется, поскольку оба распределения нормализованы, . H ( d , s ) = H ( d | s ) + H ( s ) = ^ 1 2 ( d − R s ) † N − 1 ( d − R s ) + 1 2 s † S − 1 s = ^ 1 2 [ s † ( S − 1 + R † N − 1 R ) ⏟ D − 1 s − s † R † N − 1 d ⏟ j − d † N − 1 R ⏟ j † s ] ≡ 1 2 [ s † D − 1 s − s † j − j † s ] = 1 2 [ s † D − 1 s − s † D − 1 D j ⏟ m − j † D ⏟ m † D − 1 s ] = ^ 1 2 ( s − m ) † D − 1 ( s − m ) , {\displaystyle {\begin{aligned}{\mathcal {H}}(d,s)&={\mathcal {H}}(d|s)+{\mathcal {H}}(s)\\&{\widehat {=}}{\frac {1}{2}}\,(d-R\,s)^{\dagger }N^{-1}\,(d-R\,s)+{\frac {1}{2}}\,s^{\dagger }S^{-1}\,s\\&{\widehat {=}}{\frac {1}{2}}\,\left[s^{\dagger }\underbrace {(S^{-1}+R^{\dagger }N^{-1}R)} _{D^{-1}}\,s-s^{\dagger }\underbrace {R^{\dagger }N^{-1}d} _{j}-\underbrace {d^{\dagger }N^{-1}R} _{j^{\dagger }}\,s\right]\\&\equiv {\frac {1}{2}}\,\left[s^{\dagger }D^{-1}s-s^{\dagger }j-j^{\dagger }s\right]\\&={\frac {1}{2}}\,\left[s^{\dagger }D^{-1}s-s^{\dagger }D^{-1}\underbrace {D\,j} _{m}-\underbrace {j^{\dagger }D} _{m^{\dagger }}\,D^{-1}s\right]\\&{\widehat {=}}{\frac {1}{2}}\,(s-m)^{\dagger }D^{-1}(s-m),\end{aligned}}} = ^ {\displaystyle {\widehat {=}}} s {\displaystyle s} m {\displaystyle m} D {\displaystyle D} P ( s | d ) ∝ e − H ( d , s ) ∝ e − 1 2 ( s − m ) † D − 1 ( s − m ) ∝ G ( s − m , D ) {\displaystyle {\mathcal {P}}(s|d)\propto e^{-{\mathcal {H}}(d,s)}\propto e^{-{\frac {1}{2}}\,(s-m)^{\dagger }D^{-1}(s-m)}\propto {\mathcal {G}}(s-m,D)} ∫ D s P ( s | d ) = 1 = ∫ D s G ( s − m , D ) {\displaystyle \int {\mathcal {D}}s\,{\mathcal {P}}(s|d)=1=\int {\mathcal {D}}s\,{\mathcal {G}}(s-m,D)}

Обобщенный фильтр Винера

Апостериорное среднее также известно как обобщенное решение фильтра Винера , а ковариация неопределенности — как дисперсия Винера. m = D j = ( S − 1 + R † N − 1 R ) − 1 R † N − 1 d {\displaystyle m=D\,j=(S^{-1}+R^{\dagger }N^{-1}R)^{-1}R^{\dagger }N^{-1}d} D = ( S − 1 + R † N − 1 R ) − 1 {\displaystyle D=(S^{-1}+R^{\dagger }N^{-1}R)^{-1}}

В IFT называется источником информации, поскольку он действует как исходный термин для возбуждения поля (знания), и распространителем информации, поскольку он распространяет информацию из одного места в другое в j = R † N − 1 d {\displaystyle j=R^{\dagger }N^{-1}d} D {\displaystyle D} m x = ∫ Ω d y D x y j y . {\displaystyle m_{x}=\int _{\Omega }dy\,D_{xy}j_{y}.}

Теория взаимодействия

Взаимодействующий гамильтониан

Если любое из предположений, которые ведут к свободной теории, нарушается, IFT становится взаимодействующей теорией с членами, которые имеют порядок выше квадратичного в поле сигнала. Это происходит, когда сигнал или шум не следуют гауссовой статистике, когда отклик нелинейный, когда шум зависит от сигнала или когда отклик или ковариации неопределенны.

В этом случае информационный гамильтониан может быть разложен в ряд Тейлора - Фреше ,

H ( d , s ) = 1 2 s † D − 1 s − j † s + H 0 ⏟ = H free ( d , s ) + ∑ n = 3 ∞ 1 n ! Λ x 1 . . . x n ( n ) s x 1 . . . s x n ⏟ = H int ( d , s ) , {\displaystyle {\mathcal {H}}(d,\,s)=\underbrace {{\frac {1}{2}}s^{\dagger }D^{-1}s-j^{\dagger }s+{\mathcal {H}}_{0}} _{={\mathcal {H}}_{\text{free}}(d,\,s)}+\underbrace {\sum _{n=3}^{\infty }{\frac {1}{n!}}\Lambda _{x_{1}...x_{n}}^{(n)}s_{x_{1}}...s_{x_{n}}} _{={\mathcal {H}}_{\text{int}}(d,\,s)},} где — свободный гамильтониан, который сам по себе привел бы к гауссовой апостериорной функции, а — взаимодействующий гамильтониан, который кодирует негауссовские поправки. Коэффициенты Тейлора первого и второго порядка часто отождествляются с (отрицательным) источником информации и пропагатором информации соответственно. Более высокие коэффициенты связаны с нелинейными самовзаимодействиями. H free ( d , s ) {\displaystyle {\mathcal {H}}_{\text{free}}(d,\,s)} H int ( d , s ) {\displaystyle {\mathcal {H}}_{\text{int}}(d,\,s)} − j {\displaystyle -j} D {\displaystyle D} Λ x 1 . . . x n ( n ) {\displaystyle \Lambda _{x_{1}...x_{n}}^{(n)}}

Классическое поле

Классическое поле минимизирует информационный гамильтониан и, следовательно, максимизирует апостериорную оценку: Таким образом, классическое поле является максимальной апостериорной оценкой задачи вывода поля. s cl {\displaystyle s_{\text{cl}}} ∂ H ( d , s ) ∂ s | s = s cl = 0 , {\displaystyle \left.{\frac {\partial {\mathcal {H}}(d,s)}{\partial s}}\right|_{s=s_{\text{cl}}}=0,} ∂ P ( s | d ) ∂ s | s = s cl = ∂ ∂ s e − H ( d , s ) Z ( d ) | s = s cl = − P ( d , s ) ∂ H ( d , s ) ∂ s | s = s cl ⏟ = 0 = 0 {\displaystyle \left.{\frac {\partial {\mathcal {P}}(s|d)}{\partial s}}\right|_{s=s_{\text{cl}}}=\left.{\frac {\partial }{\partial s}}\,{\frac {e^{-{\mathcal {H}}(d,s)}}{{\mathcal {Z}}(d)}}\right|_{s=s_{\text{cl}}}=-{\mathcal {P}}(d,s)\,\underbrace {\left.{\frac {\partial {\mathcal {H}}(d,s)}{\partial s}}\right|_{s=s_{\text{cl}}}} _{=0}=0} s cl {\displaystyle s_{\text{cl}}}

Критический фильтр

Проблема фильтра Винера требует, чтобы была известна двухточечная корреляция поля. Если она неизвестна, ее нужно вывести вместе с самим полем. Для этого требуется спецификация гиперприора . Часто можно предположить статистическую однородность (трансляционную инвариантность), подразумевая, что является диагональным в пространстве Фурье (для того, чтобы быть размерным декартовым пространством ). В этом случае нужно вывести только спектр мощности пространства Фурье. Учитывая дальнейшее предположение о статистической изотропии, этот спектр зависит только от длины вектора Фурье , и нужно определить только одномерный спектр . Тогда априорная ковариация поля читается в координатах пространства Фурье . S ≡ ⟨ s s † ⟩ ( s ) {\displaystyle S\equiv \langle s\,s^{\dagger }\rangle _{(s)}} P ( S ) {\displaystyle {\mathcal {P}}(S)} S {\displaystyle S} Ω = R u {\displaystyle \Omega =\mathbb {R} ^{u}} u {\displaystyle u} P s ( k → ) {\displaystyle P_{s}({\vec {k}})} k = | k → | {\displaystyle k=|{\vec {k}}|} k → {\displaystyle {\vec {k}}} P s ( k ) {\displaystyle P_{s}(k)} S k → q → = ( 2 π ) u δ ( k → − q → ) P s ( k ) {\displaystyle S_{{\vec {k}}{\vec {q}}}=(2\pi )^{u}\delta ({\vec {k}}-{\vec {q}})\,P_{s}(k)}

Если априорное значение является плоским, совместная вероятность данных и спектра равна , где снова использовалась нотация информационного пропагатора и источника проблемы фильтра Винера. Соответствующий информационный гамильтониан равен , где обозначает равенство с точностью до нерелевантных констант (здесь: константа относительно ). Минимизация этого значения относительно , ​​чтобы получить его максимальную апостериорную оценку спектра мощности, дает , где были введены среднее значение фильтра Винера и проектор спектральной полосы . Последний коммутирует с , поскольку является диагональным в пространстве Фурье. Максимальная апостериорная оценка для спектра мощности равна , следовательно, Его необходимо вычислять итеративно, так как и зависят оба от себя. В эмпирическом байесовском подходе оценка будет приниматься как заданная. Как следствие, апостериорная средняя оценка для поля сигнала является соответствующей , а ее неопределенность соответствующей в эмпирическом байесовском приближении. P s ( k ) {\displaystyle P_{s}(k)} P ( d , P s ) = ∫ D s P ( d , s , P s ) = ∫ D s P ( d | s , P s ) P ( s | P s ) P ( P s ) ∝ ∫ D s G ( d − R s , N ) G ( s , S ) ∝ 1 | S | 1 2 ∫ D s exp ⁡ [ − 1 2 ( s † D − 1 s − j † s − s † j ) ] ∝ | D | 1 2 | S | 1 2 exp ⁡ [ 1 2 j † D j ] , {\displaystyle {\begin{aligned}{\mathcal {P}}(d,P_{s})&=\int {\mathcal {D}}s\,{\mathcal {P}}(d,s,P_{s})\\&=\int {\mathcal {D}}s\,{\mathcal {P}}(d|s,P_{s})\,{\mathcal {P}}(s|P_{s})\,{\mathcal {P}}(P_{s})\\&\propto \int {\mathcal {D}}s\,{\mathcal {G}}(d-Rs,N)\,{\mathcal {G}}(s,S)\\&\propto {\frac {1}{|S|^{\frac {1}{2}}}}\int {\mathcal {D}}s\,\exp \left[-{\frac {1}{2}}\left(s^{\dagger }D^{-1}s-j^{\dagger }s-s^{\dagger }j\right)\right]\\&\propto {\frac {|D|^{\frac {1}{2}}}{|S|^{\frac {1}{2}}}}\exp \left[{\frac {1}{2}}j^{\dagger }D\,j\right],\end{aligned}}} D = ( S − 1 + R † N − 1 R ) − 1 {\displaystyle D=(S^{-1}+R^{\dagger }N^{-1}R)^{-1}} j = R † N − 1 d {\displaystyle j=R^{\dagger }N^{-1}d} H ( d , P s ) = ^ 1 2 [ ln ⁡ | S D − 1 | − j † D j ] = 1 2 T r [ ln ⁡ ( S D − 1 ) − j j † D ] , {\displaystyle {\mathcal {H}}(d,P_{s})\;{\widehat {=}}\;{\frac {1}{2}}\left[\ln |S\,D^{-1}|-j^{\dagger }D\,j\right]={\frac {1}{2}}\mathrm {Tr} \left[\ln \left(S\,D^{-1}\right)-j\,j^{\dagger }D\right],} = ^ {\displaystyle {\widehat {=}}} P s {\displaystyle P_{s}} P s {\displaystyle P_{s}} ∂ H ( d , P s ) ∂ P s ( k ) = 1 2 T r [ D S − 1 ∂ ( S D − 1 ) ∂ P s ( k ) − j j † ∂ D ∂ P s ( k ) ] = 1 2 T r [ D S − 1 ∂ ( 1 + S R † N − 1 R ) ∂ P s ( k ) + j j † D ∂ D − 1 ∂ P s ( k ) D ] = 1 2 T r [ D S − 1 ∂ S ∂ P s ( k ) R † N − 1 R + m m † ∂ S − 1 ∂ P s ( k ) ] = 1 2 T r [ ( R † N − 1 R D S − 1 − S − 1 m m † S − 1 ) ∂ S ∂ P s ( k ) ] = 1 2 ∫ ( d q 2 π ) u ∫ ( d q ′ 2 π ) u ( ( D − 1 − S − 1 ) D S − 1 − S − 1 m m † S − 1 ) q → q → ′ ∂ ( 2 π ) u δ ( q → − q → ′ ) P s ( q ) ∂ P s ( k ) = 1 2 ∫ ( d q 2 π ) u ( S − 1 − S − 1 D S − 1 − S − 1 m m † S − 1 ) q → q → δ ( k − q ) = 1 2 T r { S − 1 [ S − ( D + m m † ) ] S − 1 P k } = T r [ P k ] 2 P s ( k ) − T r [ ( D + m m † ) P k ] 2 [ P s ( k ) ] 2 = 0 , {\displaystyle {\begin{aligned}{\frac {\partial {\mathcal {H}}(d,P_{s})}{\partial P_{s}(k)}}&={\frac {1}{2}}\mathrm {Tr} \left[D\,S^{-1}\,{\frac {\partial \left(S\,D^{-1}\right)}{\partial P_{s}(k)}}-j\,j^{\dagger }{\frac {\partial D}{\partial P_{s}(k)}}\right]\\&={\frac {1}{2}}\mathrm {Tr} \left[D\,S^{-1}\,{\frac {\partial \left(1+S\,R^{\dagger }N^{-1}R\right)}{\partial P_{s}(k)}}+j\,j^{\dagger }D\,{\frac {\partial D^{-1}}{\partial P_{s}(k)}}\,D\right]\\&={\frac {1}{2}}\mathrm {Tr} \left[D\,S^{-1}\,{\frac {\partial S}{\partial P_{s}(k)}}R^{\dagger }N^{-1}R+m\,m^{\dagger }\,{\frac {\partial S^{-1}}{\partial P_{s}(k)}}\right]\\&={\frac {1}{2}}\mathrm {Tr} \left[\left(R^{\dagger }N^{-1}R\,D\,S^{-1}-S^{-1}m\,m^{\dagger }\,S^{-1}\right)\,{\frac {\partial S}{\partial P_{s}(k)}}\right]\\&={\frac {1}{2}}\int \left({\frac {dq}{2\pi }}\right)^{u}\int \left({\frac {dq'}{2\pi }}\right)^{u}\left(\left(D^{-1}-S^{-1}\right)\,D\,S^{-1}-S^{-1}m\,m^{\dagger }\,S^{-1}\right)_{{\vec {q}}{\vec {q}}'}\,{\frac {\partial (2\pi )^{u}\delta ({\vec {q}}-{\vec {q}}')\,P_{s}(q)}{\partial P_{s}(k)}}\\&={\frac {1}{2}}\int \left({\frac {dq}{2\pi }}\right)^{u}\left(S^{-1}-S^{-1}D\,S^{-1}-S^{-1}m\,m^{\dagger }\,S^{-1}\right)_{{\vec {q}}{\vec {q}}}\,\delta (k-q)\\&={\frac {1}{2}}\mathrm {Tr} \left\{S^{-1}\left[S-\left(D+m\,m^{\dagger }\right)\right]\,S^{-1}\mathbb {P} _{k}\right\}\\&={\frac {\mathrm {Tr} \left[\mathbb {P} _{k}\right]}{2\,P_{s}(k)}}-{\frac {\mathrm {Tr} \left[\left(D+m\,m^{\dagger }\right)\,\mathbb {P} _{k}\right]}{2\,\left[P_{s}(k)\right]^{2}}}=0,\end{aligned}}} m = D j {\displaystyle m=D\,j} ( P k ) q → q → ′ ≡ ( 2 π ) u δ ( q → − q → ′ ) δ ( | q → | − k ) {\displaystyle (\mathbb {P} _{k})_{{\vec {q}}{\vec {q}}'}\equiv (2\pi )^{u}\delta ({\vec {q}}-{\vec {q}}')\,\delta (|{\vec {q}}|-k)} S − 1 {\displaystyle S^{-1}} ( S − 1 ) k → q → = ( 2 π ) u δ ( k → − q → ) [ P s ( k ) ] − 1 {\displaystyle (S^{-1})_{{\vec {k}}{\vec {q}}}=(2\pi )^{u}\delta ({\vec {k}}-{\vec {q}})\,[P_{s}(k)]^{-1}} P s ( k ) = T r [ ( m m † + D ) P k ] T r [ P k ] . {\displaystyle P_{s}(k)={\frac {\mathrm {Tr} \left[\left(m\,m^{\dagger }+D\right)\,\mathbb {P} _{k}\right]}{\mathrm {Tr} \left[\mathbb {P} _{k}\right]}}.} m = D j {\displaystyle m=D\,j} D = ( S − 1 + R † N − 1 R ) − 1 {\displaystyle D=(S^{-1}+R^{\dagger }N^{-1}R)^{-1}} P s {\displaystyle P_{s}} P s {\displaystyle P_{s}} m {\displaystyle m} D {\displaystyle D}

Полученный нелинейный фильтр называется критическим фильтром . [4] Обобщение формулы оценки спектра мощности как показывает пороги восприятия для , что означает, что дисперсия данных в полосе Фурье должна превысить ожидаемый уровень шума на определенный порог, прежде чем реконструкция сигнала станет ненулевой для этой полосы. Всякий раз, когда дисперсия данных немного превышает этот порог, реконструкция сигнала переходит на конечный уровень возбуждения, аналогично фазовому переходу первого рода в термодинамических системах. Для фильтра с восприятием сигнала начинается непрерывно, как только дисперсия данных превысит уровень шума. Исчезновение прерывистого восприятия при аналогично прохождению термодинамической системой критической точки . Отсюда и название критический фильтр. P s ( k ) = T r [ ( m m † + δ D ) P k ] T r [ P k ] {\displaystyle P_{s}(k)={\frac {\mathrm {Tr} \left[\left(m\,m^{\dagger }+\delta \,D\right)\,\mathbb {P} _{k}\right]}{\mathrm {Tr} \left[\mathbb {P} _{k}\right]}}} δ < 1 {\displaystyle \delta <1} m {\displaystyle m} δ = 1 {\displaystyle \delta =1} δ = 1 {\displaystyle \delta =1}

Критический фильтр, его расширения для нелинейных измерений и включение априорных значений неплоского спектра позволили применить IFT к реальным задачам вывода сигналов, для которых ковариация сигнала обычно неизвестна априори.

Примеры применения IFT

Радиоинтерферометрическое изображение радиогалактик в скоплении галактик Abell 2219. Изображения были построены с помощью обратной проекции данных (вверху), алгоритма CLEAN (в середине) и алгоритма RESOLVE (внизу). Отрицательные и, следовательно, нефизические потоки показаны белым цветом.

Обобщенный фильтр Винера, возникающий в свободном IFT, широко используется в обработке сигналов. Для ряда приложений были получены алгоритмы, явно основанные на IFT. Многие из них реализованы с использованием библиотеки Numerical Information Field Theory (NIFTy).

  • D³PO — это код для Denoising, Deconvolution, and Decomposing Photon Observations . Он реконструирует изображения из отдельных событий подсчета фотонов с учетом статистики Пуассона подсчетов и функции отклика прибора. Он разделяет излучение неба на изображение диффузного излучения и одно из точечных источников, используя различную корреляционную структуру и статистику двух компонентов для их разделения. D³PO был применен к данным спутников Fermi и RXTE .
  • RESOLVE — это байесовский алгоритм для визуализации синтеза апертуры в радиоастрономии. RESOLVE похож на D³PO, но предполагает гауссово правдоподобие и функцию отклика пространства Фурье. Он был применен к данным Very Large Array .
  • PySESA — это фреймворк Python для пространственно-явного спектрального анализа, предназначенный для пространственно-явного спектрального анализа облаков точек и геопространственных данных.

Продвинутая теория

Для решения задач IFT можно использовать многие методы квантовой теории поля, такие как диаграммы Фейнмана, эффективные действия и формализм полевых операторов.

Диаграммы Фейнмана

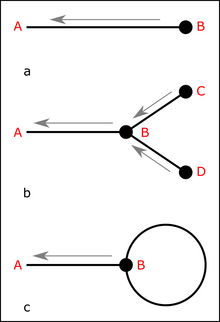
Первые три диаграммы Фейнмана, вносящие вклад в апостериорную среднюю оценку поля. Линия выражает информационный пропагатор, точка в конце линии — источник информации, а вершина — член взаимодействия. Первая диаграмма кодирует фильтр Винера, вторая — нелинейную коррекцию, а третья — поправку неопределенности к фильтру Винера.

В случае, если коэффициенты взаимодействия в разложении Тейлора - Фреше информационного гамильтониана малы, логарифмическая статсумма или свободная энергия Гельмгольца может быть асимптотически разложена по этим коэффициентам. Свободный гамильтониан определяет среднее значение и дисперсию гауссовского распределения , по которому интегрируется разложение. Это приводит к сумме по множеству всех связанных диаграмм Фейнмана . Из свободной энергии Гельмгольца любой связанный момент поля может быть вычислен с помощью Ситуации, в которых существуют малые параметры разложения, необходимые для сходимости такого диаграммного разложения, задаются почти гауссовыми сигнальными полями, где негауссовость статистики поля приводит к малым коэффициентам взаимодействия . Например, статистика реликтового космического излучения почти гауссова, с небольшим количеством негауссовостей, которые, как полагают, были засеяны во время инфляционной эпохи в ранней Вселенной . Λ ( n ) {\displaystyle \Lambda ^{(n)}} H ( d , s ) = 1 2 s † D − 1 s − j † s + H 0 ⏟ = H free ( d , s ) + ∑ n = 3 ∞ 1 n ! Λ x 1 . . . x n ( n ) s x 1 . . . s x n ⏟ = H int ( d , s ) , {\displaystyle {\mathcal {H}}(d,\,s)=\underbrace {{\frac {1}{2}}s^{\dagger }D^{-1}s-j^{\dagger }s+{\mathcal {H}}_{0}} _{={\mathcal {H}}_{\text{free}}(d,\,s)}+\underbrace {\sum _{n=3}^{\infty }{\frac {1}{n!}}\Lambda _{x_{1}...x_{n}}^{(n)}s_{x_{1}}...s_{x_{n}}} _{={\mathcal {H}}_{\text{int}}(d,\,s)},} ln ⁡ Z ( d ) = ln ⁡ ∫ D s e − H ( d , s ) = ∑ c ∈ C c {\displaystyle \ln {\mathcal {Z}}(d)=\ln \int {\mathcal {D}}s\,e^{-{\mathcal {H}}(d,s)}=\sum _{c\in C}c} m = D j {\displaystyle m=D\,j} D {\displaystyle D} G ( s − m , D ) {\displaystyle {\mathcal {G}}(s-m,D)} C {\displaystyle C} ⟨ s x 1 … s x n ⟩ ( s | d ) c = ∂ n ln ⁡ Z ∂ j x 1 … ∂ j x n . {\displaystyle \langle s_{x_{1}}\ldots s_{x_{n}}\rangle _{(s|d)}^{\text{c}}={\frac {\partial ^{n}\ln {\mathcal {Z}}}{\partial j_{x_{1}}\ldots \partial j_{x_{n}}}}.} Λ ( n ) {\displaystyle \Lambda ^{(n)}}

Эффективное действие

Для того чтобы иметь стабильные числовые данные для задач IFT, необходим функционал поля, который при минимизации обеспечивает апостериорное среднее поле. Оно задается эффективным действием или свободной энергией Гиббса поля. Свободная энергия Гиббса может быть построена из свободной энергии Гельмгольца с помощью преобразования Лежандра . В IFT она задается разностью внутренней информационной энергии и энтропии Шеннона для температуры , где используется гауссовское апостериорное приближение с приближенными данными, содержащими среднее значение и дисперсию поля. [5] G {\displaystyle G} U = ⟨ H ( d , s ) ⟩ P ′ ( s | d ′ ) {\displaystyle U=\langle {\mathcal {H}}(d,s)\rangle _{{\mathcal {P}}'(s|d')}} S = − ∫ D s P ′ ( s | d ′ ) ln ⁡ P ′ ( s | d ′ ) {\displaystyle {\mathcal {S}}=-\int {\mathcal {D}}s\,{\mathcal {P}}'(s|d')\,\ln {\mathcal {P}}'(s|d')} T = 1 {\displaystyle T=1} P ′ ( s | d ′ ) = G ( s − m , D ) {\displaystyle {\mathcal {P}}'(s|d')={\mathcal {G}}(s-m,D)} d ′ = ( m , D ) {\displaystyle d'=(m,D)}

Свободная энергия Гиббса тогда равна расхождению Кульбака-Лейблера между приближенным и точным апостериорным распределением плюс свободная энергия Гельмгольца. Поскольку последнее не зависит от приближенных данных , минимизация свободной энергии Гиббса эквивалентна минимизации расхождения Кульбака-Лейблера между приближенным и точным апостериорным распределением. Таким образом, эффективный подход IFT эквивалентен вариационным байесовским методам , которые также минимизируют расхождение Кульбака-Лейблера между приближенным и точным апостериорным распределением. G ( m , D ) = U ( m , D ) − T S ( m , D ) = ⟨ H ( d , s ) + ln ⁡ P ′ ( s | d ′ ) ⟩ P ′ ( s | d ′ ) = ∫ D s P ′ ( s | d ′ ) ln ⁡ P ′ ( s | d ′ ) P ( d , s ) = ∫ D s P ′ ( s | d ′ ) ln ⁡ P ′ ( s | d ′ ) P ( s | d ) P ( d ) = ∫ D s P ′ ( s | d ′ ) ln ⁡ P ′ ( s | d ′ ) P ( s | d ) − ln P ( d ) = KL ( P ′ ( s | d ′ ) | | P ( s | d ) ) − ln ⁡ Z ( d ) , {\displaystyle {\begin{aligned}G(m,D)&=U(m,D)-T\,{\mathcal {S}}(m,D)\\&=\langle {\mathcal {H}}(d,s)+\ln {\mathcal {P}}'(s|d')\rangle _{{\mathcal {P}}'(s|d')}\\&=\int {\mathcal {D}}s\,{\mathcal {P}}'(s|d')\,\ln {\frac {{\mathcal {P}}'(s|d')}{{\mathcal {P}}(d,s)}}\\&=\int {\mathcal {D}}s\,{\mathcal {P}}'(s|d')\,\ln {\frac {{\mathcal {P}}'(s|d')}{{\mathcal {P}}(s|d)\,{\mathcal {P}}(d)}}\\&=\int {\mathcal {D}}s\,{\mathcal {P}}'(s|d')\,\ln {\frac {{\mathcal {P}}'(s|d')}{{\mathcal {P}}(s|d)}}-\ln \,{\mathcal {P}}(d)\\&={\text{KL}}({\mathcal {P}}'(s|d')||{\mathcal {P}}(s|d))-\ln {\mathcal {Z}}(d),\end{aligned}}} KL ( P ′ , P ) {\displaystyle {\text{KL}}({\mathcal {P}}',{\mathcal {P}})} d ′ = ( m , D ) {\displaystyle d'=(m,D)}

Минимизация свободной энергии Гиббса обеспечивает аппроксимацию апостериорного среднего поля , тогда как минимизация информационного гамильтониана обеспечивает максимальное апостериорное поле. Поскольку последний, как известно, переобучает шум, первый обычно является лучшей оценкой поля. ⟨ s ⟩ ( s | d ) = ∫ D s s P ( s | d ) , {\displaystyle \langle s\rangle _{(s|d)}=\int {\mathcal {D}}s\,s\,{\mathcal {P}}(s|d),}

Операторный формализм

Расчет свободной энергии Гиббса требует вычисления гауссовых интегралов по информационному гамильтониану, поскольку внутренняя информационная энергия равна Такие интегралы можно вычислить с помощью формализма оператора поля, [6] в котором есть оператор поля. Это генерирует выражение поля внутри интеграла, если применяется к гауссовой функции распределения, и любую более высокую степень поля, если применяется несколько раз, Если информационный гамильтониан является аналитическим, все его члены могут быть сгенерированы с помощью оператора поля Поскольку оператор поля не зависит от самого поля, его можно вытащить из интеграла по траектории конструкции внутренней информационной энергии, где следует рассматривать как функционал, который всегда возвращает значение независимо от значения его входа . Результирующее выражение можно вычислить, коммутируя аннигилятор среднего поля справа от выражения, где они исчезают, поскольку . Аннигилятор среднего поля коммутирует со средним полем как U ( m , D ) = ⟨ H ( d , s ) ⟩ P ′ ( s | d ′ ) = ∫ D s H ( d , s ) G ( s − m , D ) . {\displaystyle U(m,D)=\langle {\mathcal {H}}(d,s)\rangle _{{\mathcal {P}}'(s|d')}=\int {\mathcal {D}}s\,{\mathcal {H}}(d,s)\,{\mathcal {G}}(s-m,D).} O m = m + D d d m {\displaystyle O_{m}=m+D\,{\frac {\mathrm {d} }{\mathrm {d} m}}} s {\displaystyle s} O m G ( s − m , D ) = ( m + D d d m ) 1 | 2 π D | 1 2 exp ⁡ [ − 1 2 ( s − m ) † D − 1 ( s − m ) ] = ( m + D D − 1 ( s − m ) ) 1 | 2 π D | 1 2 exp ⁡ [ − 1 2 ( s − m ) † D − 1 ( s − m ) ] = s G ( s − m , D ) , {\displaystyle {\begin{aligned}O_{m}\,{\mathcal {G}}(s-m,D)&=(m+D\,{\frac {\mathrm {d} }{\mathrm {d} m}})\,{\frac {1}{|2\pi D|^{\frac {1}{2}}}}\,\exp \left[-{\frac {1}{2}}(s-m)^{\dagger }D^{-1}(s-m)\right]\\&=(m+D\,D^{-1}(s-m))\,{\frac {1}{|2\pi D|^{\frac {1}{2}}}}\,\exp \left[-{\frac {1}{2}}(s-m)^{\dagger }D^{-1}(s-m)\right]\\&=s\,{\mathcal {G}}(s-m,D),\end{aligned}}} ( O m ) n G ( s − m , D ) = s n G ( s − m , D ) . {\displaystyle {\begin{aligned}(O_{m})^{n}\,{\mathcal {G}}(s-m,D)&=s^{n}\,{\mathcal {G}}(s-m,D).\end{aligned}}} H ( d , O m ) G ( s − m , D ) = H ( d , s ) G ( s − m , D ) . {\displaystyle {\mathcal {H}}(d,O_{m})\,{\mathcal {G}}(s-m,D)={\mathcal {H}}(d,s)\,{\mathcal {G}}(s-m,D).} s {\displaystyle s} U ( m , D ) = ∫ D s H ( d , O m ) G ( s − m , D ) = H ( d , O m ) ∫ D s G ( s − m , D ) = H ( d , O m ) 1 m , {\displaystyle U(m,D)=\int {\mathcal {D}}s\,{\mathcal {H}}(d,O_{m})\,{\mathcal {G}}(s-m,D)={\mathcal {H}}(d,O_{m})\int {\mathcal {D}}s\,{\mathcal {G}}(s-m,D)={\mathcal {H}}(d,O_{m})\,1_{m},} 1 m = 1 {\displaystyle 1_{m}=1} 1 {\displaystyle 1} m {\displaystyle m} D d d m {\displaystyle D\,{\frac {\mathrm {d} }{\mathrm {d} m}}} d d m 1 m = 0 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} m}}\,1_{m}=0} D d d m {\displaystyle D\,{\frac {\mathrm {d} }{\mathrm {d} m}}} [ D d d m , m ] = D d d m m − m D d d m = D + m D d d m − m D d d m = D . {\displaystyle \left[D\,{\frac {\mathrm {d} }{\mathrm {d} m}},m\right]=D\,{\frac {\mathrm {d} }{\mathrm {d} m}}\,m-m\,D\,{\frac {\mathrm {d} }{\mathrm {d} m}}=D+m\,D\,{\frac {\mathrm {d} }{\mathrm {d} m}}-m\,D\,{\frac {\mathrm {d} }{\mathrm {d} m}}=D.}

Используя формализм оператора поля, можно рассчитать свободную энергию Гиббса, что позволяет сделать (приближенный) вывод апостериорного среднего поля посредством численной надежной минимизации функционала.

История

Книгу Норберта Винера [7] можно считать одной из первых работ по полевым выводам. Использование интегралов по траектории для полевых выводов было предложено рядом авторов, например, Эдмундом Берчингером [8] или Уильямом Биалеком и А. Зее. [9] Связь теории поля и байесовских рассуждений была явно выражена Йоргом Леммом. [10] Термин «теория информационного поля» был придуман Торстеном Энслином. [11] См. последнюю ссылку для получения дополнительной информации об истории IFT.

Смотрите также

Ссылки

  1. ^ Энслин, Торстен (2013). «Теория информационного поля». Труды конференции AIP . 1553 (1): 184–191. arXiv : 1301.2556 . Bibcode : 2013AIPC.1553..184E. doi : 10.1063/1.4819999.
  2. ^ Энслин, Торстен А. (2019). «Теория информации для полей». Аннален дер Физик . 531 (3): 1800127. arXiv : 1804.03350 . Бибкод : 2019АнП...53100127E. дои : 10.1002/andp.201800127.
  3. ^ "Теория информационного поля". Общество Макса Планка . Получено 13 ноября 2014 г.
  4. ^ Энслин, Торстен А.; Фроммерт, Мона (2011-05-19). "Реконструкция сигналов с неизвестными спектрами в теории информационного поля с неопределенностью параметров". Physical Review D. 83 ( 10): 105014. arXiv : 1002.2928 . Bibcode : 2011PhRvD..83j5014E. doi : 10.1103/PhysRevD.83.105014.
  5. ^ Энслин, Торстен А. (2010). «Вывод с минимальной свободной энергией Гиббса в теории информационного поля». Physical Review E. 82 ( 5): 051112. arXiv : 1004.2868 . Bibcode : 2010PhRvE..82e1112E. doi : 10.1103/physreve.82.051112. PMID  21230442.
  6. ^ Лейке, Реймар Х.; Энслин, Торстен А. (16.11.2016). «Операторное исчисление для теории информационного поля». Physical Review E. 94 ( 5): 053306. arXiv : 1605.00660 . Bibcode : 2016PhRvE..94e3306L. doi : 10.1103/PhysRevE.94.053306. PMID  27967173.
  7. ^ Винер, Норберт (1964). Экстраполяция, интерполяция и сглаживание стационарных временных рядов с инженерными приложениями (Пятое издание). Кембридж, Массачусетс: Technology Press Массачусетского технологического института. ISBN 0262730057. OCLC  489911338.
  8. ^ Берчингер, Эдмунд (декабрь 1987 г.). «Методы интегралов по путям для первичных возмущений плотности — выборка ограниченных гауссовых случайных полей». The Astrophysical Journal . 323 : L103–L106. Bibcode :1987ApJ...323L.103B. doi : 10.1086/185066 . ISSN  0004-637X.
  9. ^ Биалек, Уильям; Зи, А. (1988-09-26). «Понимание эффективности человеческого восприятия». Physical Review Letters . 61 (13): 1512–1515. Bibcode : 1988PhRvL..61.1512B. doi : 10.1103/PhysRevLett.61.1512. PMID  10038817.
  10. ^ Лемм, Йорг К. (2003). Байесовская теория поля . Балтимор, Мэриленд: Johns Hopkins University Press. ISBN 9780801872204. OCLC  52762436.
  11. ^ Энслин, Торстен А.; Фроммерт, Мона; Китаура, Франциско С. (2009-11-09). "Теория информационного поля для реконструкции космологических возмущений и нелинейного анализа сигналов". Physical Review D. 80 ( 10): 105005. arXiv : 0806.3474 . Bibcode : 2009PhRvD..80j5005E. doi : 10.1103/PhysRevD.80.105005.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Information_field_theory&oldid=1256010298"