Гиперболическое дерево
Математическое дерево в гиперболической плоскости

Гиперболическое дерево (часто сокращенно гипердерево ) — это метод визуализации информации и рисования графиков, вдохновленный гиперболической геометрией .

Базовое гиперболическое дерево. Узлы в фокусе размещаются в центре и получают больше места, а узлы вне фокуса сжимаются вблизи границ.
При фокусировке на другом узле он и его дочерние элементы перемещаются в центр диска, а неинтересные части дерева сжимаются.

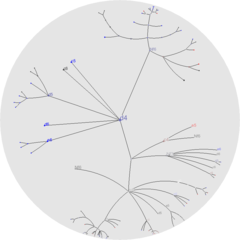
Отображение иерархических данных в виде дерева страдает от визуального беспорядка, поскольку количество узлов на уровне может расти экспоненциально. Для простого бинарного дерева максимальное количество узлов на уровне n равно 2 n , тогда как количество узлов для деревьев с большим количеством ветвлений растет гораздо быстрее. Таким образом, для отображения дерева в виде диаграммы узлов-связей требуется экспоненциальное количество места.

Один из подходов заключается в использовании гиперболического дерева , впервые представленного Лэмпингом и др. [1] Гиперболические деревья используют гиперболическое пространство , которое по своей сути имеет «больше места», чем евклидово пространство. Например, линейное увеличение радиуса круга в евклидовом пространстве увеличивает его окружность линейно, в то время как тот же круг в гиперболическом пространстве будет иметь свою окружность, увеличивающуюся экспоненциально. Использование этого свойства позволяет размещать дерево в гиперболическом пространстве незагроможденным образом: размещение узла достаточно далеко от его родителя дает узлу почти такое же количество пространства, как и его родителю, для размещения его собственных дочерних элементов.

Отображение гиперболического дерева обычно использует модель диска Пуанкаре гиперболической геометрии, хотя модель Клейна-Бельтрами также может быть использована. Оба отображают всю гиперболическую плоскость внутри единичного диска, делая все дерево видимым сразу. Единичный диск дает вид плоскости через линзу «рыбий глаз», делая больший акцент на узлах, которые находятся в фокусе, и отображая узлы, которые находятся дальше от фокуса ближе к границе диска. Обход гиперболического дерева требует преобразований Мёбиуса пространства, помещая новые узлы в фокус и перемещая более высокие уровни иерархии за пределы поля зрения.

Гиперболические деревья были запатентованы в США компанией Xerox в 1996 году, но срок действия патента с тех пор истек. [2]

Смотрите также

Ссылки

  1. ^ Лампинг, Джон Огден; Рао, Рамана; Пиролли, Питер (май 1995 г.). Метод фокус+контекст на основе гиперболической геометрии для визуализации больших иерархий. Труды конференции ACM по человеческому фактору в вычислительных системах (CHI 1995). стр.  401–408 . CiteSeerX  10.1.1.20.1530 . doi :10.1145/223904.223956. Архивировано из оригинала 2017-05-10 . Получено 2021-04-13 .
  2. ^ Патент США 5590250, Лэмпинг; Джон О. и Рао; Рамана Б., «Расположение узлово-связующих структур в пространстве с отрицательной кривизной», переданный корпорации Xerox 
На Викискладе есть медиафайлы по теме «Гиперболические деревья» .
  • d3-hypertree – реализация гиперболического дерева HTML5, лицензировано MIT
  • Гиперболическое древо жизни – визуализация древа жизни с открытым исходным кодом с использованием набора данных Open Tree of Life
  • Зеленое дерево жизни – Древо жизни – Калифорнийский университет в Беркли и гербарии Джепсона
  • Древо жизни. Аналогично предыдущему, но с картинками.
  • RogueViz поддерживает гиперболические деревья.
Получено с "https://en.wikipedia.org/w/index.php?title=Гиперболическое_дерево&oldid=1194896312"