Свойство расширения гомотопии

В математике , в области алгебраической топологии , свойство гомотопического расширения указывает, какие гомотопии, определенные на подпространстве, могут быть расширены до гомотопии, определенной на большем пространстве. Свойство гомотопического расширения корасслоений является двойственным свойству гомотопического подъема , которое используется для определения расслоений .

Пусть будет топологическим пространством , и пусть . Мы говорим, что пара имеет свойство гомотопического расширения , если для данной гомотопии и отображения , таких что , то существует расширение до гомотопии , такой что . ^[1]${\displaystyle X\,\!}$${\displaystyle A\подмножество X}$${\displaystyle (X,A)\,\!}$${\displaystyle f_{\bullet }\colon A\rightarrow Y^{I}}$${\displaystyle {\tilde {f}}_{0}\двоеточие X\rightarrow Y}$$${\displaystyle {\tilde {f}}_{0}\circ \iota =\left.{\tilde {f}}_{0}\right|_{A}=f_{0}=\pi _{0}\circ f_{\bullet },}$$${\displaystyle f_{\bullet }}$${\displaystyle {\tilde {f}}_{\bullet }\colon X\rightarrow Y^{I}}$${\displaystyle {\tilde {f}}_{\bullet }\circ \iota =\left.{\tilde {f}}_{\bullet }\right|_{A}=f_{\bullet }}$

То есть пара обладает свойством гомотопического расширения, если любое отображение может быть расширено до отображения (т.е. и согласуется с их общей областью определения).${\displaystyle (X,A)\,\!}$${\displaystyle G\colon ((X\times \{0\})\cup (A\times I))\rightarrow Y}$${\displaystyle G'\двоеточие X\times I\rightarrow Y}$${\displaystyle Г\,\!}$${\displaystyle Г'\,\!}$

Если пара обладает этим свойством только для определенной области значений , мы говорим, что она обладает свойством расширения гомотопии относительно .${\displaystyle Y\,\!}$${\displaystyle (X,A)\,\!}$${\displaystyle Y\,\!}$

Свойство расширения гомотопии изображено на следующей диаграмме.

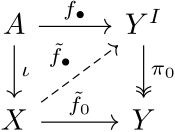
Если приведенная выше диаграмма (без пунктирной карты) коммутирует (это эквивалентно условиям выше), то пара (X,A) имеет свойство расширения гомотопии, если существует карта, которая делает диаграмму коммутативной. При карринге обратите внимание, что гомотопии, выраженные как карты, находятся в естественной биекции с выражениями как карты .${\displaystyle {\tilde {f}}_{\bullet }}$${\displaystyle {\tilde {f}}_{\bullet }\двоеточие X\до Y^{I}}$${\displaystyle {\tilde {f}}_{\bullet }\colon X\times I\to Y}$

Обратите внимание, что эта диаграмма является двойственной (противоположной) диаграмме свойства гомотопического подъема ; эта двойственность широко именуется двойственностью Экмана–Хилтона .

• Если — клеточный комплекс и — подкомплекс , то пара обладает свойством гомотопического расширения.${\displaystyle X\,\!}$${\displaystyle А\,\!}$${\displaystyle X\,\!}$${\displaystyle (X,A)\,\!}$
• Пара обладает свойством гомотопического расширения тогда и только тогда, когда является ретрактом${\displaystyle (X,A)\,\!}$${\displaystyle (X\times \{0\}\cup A\times I)}$${\displaystyle X\times I.}$

Если обладает свойством гомотопического расширения, то простое отображение включения является корасслоением .${\displaystyle (X,A)}$${\displaystyle \iota \colon A\to X}$

На самом деле, если рассмотреть любое корасслоение , то мы имеем , которое гомеоморфно своему образу при . Это подразумевает, что любое корасслоение можно рассматривать как отображение включения, и, следовательно, его можно рассматривать как обладающее свойством гомотопического расширения.${\displaystyle \iota \двоеточие от Y\до Z}$${\displaystyle \mathbf {\mathit {Y}} }$${\displaystyle \йота}$

• Свойство подъема гомотопии

• Хэтчер, Аллен (2002). Алгебраическая топология. Cambridge University Press. ISBN 0-521-79540-0.
• «Свойство расширения гомотопии». PlanetMath .