Гомоклиническая орбита

В изучении динамических систем гомоклиническая орбита — это путь через фазовое пространство , который соединяет седловую точку равновесия с собой. Точнее, гомоклиническая орбита лежит в пересечении устойчивого многообразия и неустойчивого многообразия равновесия. Это гетероклиническая орбита — путь между любыми двумя точками равновесия, — в котором конечные точки совпадают.

Рассмотрим непрерывную динамическую систему, описываемую обыкновенным дифференциальным уравнением

${\displaystyle {\dot {x}}=f(x)}$

Предположим, что существует равновесие при , тогда решение является гомоклинической орбитой, если${\displaystyle x=x_{0}}$${\displaystyle \Фи (т)}$

${\displaystyle \Phi (t)\rightarrow x_{0}\quad \mathrm {as} \quad t\rightarrow \pm \infty }$

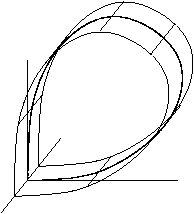
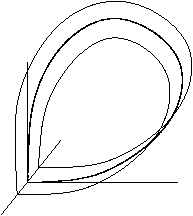
Если фазовое пространство имеет три или более измерений , то важно учитывать топологию неустойчивого многообразия седловой точки. На рисунках показаны два случая. Во-первых, когда устойчивое многообразие топологически является цилиндром , а во-вторых, когда неустойчивое многообразие топологически является лентой Мёбиуса ; в этом случае гомоклиническая орбита называется скрученной .

Гомоклинические орбиты и гомоклинические точки определяются таким же образом для итерированных функций , как пересечение устойчивого множества и неустойчивого множества некоторой неподвижной точки или периодической точки системы.

Мы также имеем понятие гомоклинической орбиты при рассмотрении дискретных динамических систем. В таком случае, если является диффеоморфизмом многообразия , мы говорим, что является гомоклинической точкой, если она имеет то же самое прошлое и будущее - более конкретно, если существует неподвижная (или периодическая) точка, такая что${\displaystyle f:M\rightarrow M}$ ${\displaystyle М}$${\displaystyle x}$${\displaystyle p}$

${\displaystyle \lim _{n\rightarrow \pm \infty }f^{n}(x)=p.}$

Существование одной гомоклинической точки подразумевает существование бесконечного их числа. ^[1] Это следует из его определения: пересечение устойчивого и неустойчивого множеств. Оба множества инвариантны по определению, что означает, что прямая итерация гомоклинической точки находится как на устойчивом, так и на неустойчивом множестве. При итерации N раз отображение приближается к точке равновесия по устойчивому множеству, но в каждой итерации оно также находится на неустойчивом многообразии, что показывает это свойство.

Это свойство предполагает, что сложная динамика возникает из-за существования гомоклинической точки. Действительно, Смейл (1967) ^[2] показал, что эти точки приводят к динамике, подобной подковообразной карте , которая связана с хаосом.

Используя разбиение Маркова , долговременное поведение гиперболической системы можно изучать с помощью методов символической динамики . В этом случае гомоклиническая орбита имеет особенно простое и ясное представление. Предположим, что — конечный набор символов M. Динамика точки x тогда представляется в виде двунаправленной бесконечной строки символов ${\displaystyle S=\{1,2,\ldots ,M\}}$

${\displaystyle \sigma =\{(\ldots ,s_{-1},s_{0},s_{1},\ldots ):s_{k}\in S\;\forall k\in \mathbb {Z} \}}$

Периодическая точка системы — это просто повторяющаяся последовательность букв. Гетероклиническая орбита — это соединение двух различных периодических орбит. Она может быть записана как

${\displaystyle p^{\omega }s_{1}s_{2}\cdots s_{n}q^{\omega }}$

где — последовательность символов длины k (конечно, ), а — другая последовательность символов длины m (аналогично, ). Обозначение просто обозначает повторение p бесконечное число раз. Таким образом, гетероклиническую орбиту можно понимать как переход от одной периодической орбиты к другой. Напротив, гомоклиническую орбиту можно записать как ${\displaystyle p=t_{1}t_{2}\cdots t_{k}}$${\displaystyle t_{i}\in S}$${\displaystyle q=r_{1}r_{2}\cdots r_{m}}$${\displaystyle r_{i}\in S}$${\displaystyle p^{\omega }}$

${\displaystyle p^{\omega }s_{1}s_{2}\cdots s_{n}p^{\omega }}$

причем промежуточная последовательность непуста и, конечно, не равна p , так как в противном случае орбита была бы просто .${\displaystyle s_{1}s_{2}\cdots s_{n}}$${\displaystyle p^{\omega }}$

• Гетероклиническая орбита
• Гомоклиническая бифуркация

• Джон Гукенхаймер и Филип Холмс , Нелинейные колебания, динамические системы и бифуркации векторных полей (Прикладные математические науки, том 42), Springer

• Гомоклинические орбиты на карте Хенона с Java-апплетами и комментариями