Модель мышц Хилла
В биомеханике модель мышц Хилла относится к 3-элементной модели , состоящей из сократительного элемента (CE) последовательно с легкозатухающим упругим пружинным элементом (SE) и параллельно с легкозатухающим упругим параллельным элементом (PE). В этой модели расчетное соотношение силы и скорости для элемента CE обычно моделируется тем, что обычно называется уравнением Хилла, которое было основано на тщательных экспериментах с тетанизированным сокращением мышц , где измерялись различные мышечные нагрузки и связанные с ними скорости. Они были выведены известным физиологом Арчибальдом Вивианом Хиллом , который к 1938 году, когда он представил эту модель и уравнение, уже получил Нобелевскую премию по физиологии. Он продолжал публиковаться в этой области до 1970 года. Существует много форм основных моделей «на основе Хилла» или «типа Хилла», и сотни публикаций использовали эту модельную структуру для экспериментальных и имитационных исследований. Большинство основных пакетов моделирования опорно-двигательного аппарата используют эту модель.
Уравнение силы-скорости А. В. Хилла для тетанизированной мышцы
Это популярное уравнение состояния, применимое к скелетной мышце , которая была стимулирована для демонстрации тетанического сокращения . Оно связывает напряжение со скоростью с учетом внутренней термодинамики . Уравнение имеет вид
где
- это напряжение (или нагрузка) в мышце
- это скорость сокращения
- максимальное изометрическое напряжение (или нагрузка), создаваемое в мышце
- коэффициент сокращения тепла
- максимальная скорость, когда
Хотя уравнение Хилла очень похоже на уравнение Ван-дер-Ваальса , первое имеет единицы рассеивания энергии , а второе — единицы энергии . Уравнение Хилла показывает, что соотношение между F и v является гиперболическим . Поэтому, чем выше нагрузка, приложенная к мышце, тем ниже скорость сокращения. Аналогично, чем выше скорость сокращения, тем ниже напряжение в мышце. Было обнаружено, что эта гиперболическая форма соответствует эмпирической константе только во время изотонических сокращений вблизи длины покоя. [1]
Напряжение мышц уменьшается по мере увеличения скорости сокращения. Эта особенность объясняется двумя основными причинами. Основной, по-видимому, является потеря напряжения, поскольку поперечные мостики в сократительном элементе затем восстанавливаются в укороченном состоянии. Второй причиной, по-видимому, является вязкость жидкости как в сократительном элементе, так и в соединительной ткани. Какой бы ни была причина потери напряжения, это вязкое трение и, следовательно, его можно смоделировать как демпфер жидкости . [2]
Трёхэлементная модель

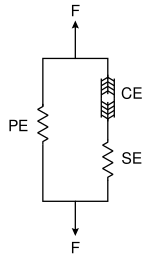
Трехэлементная модель мышцы Хилла представляет собой представление механического ответа мышцы. Модель состоит из сократительного элемента ( CE ) и двух нелинейных пружинных элементов , один последовательно ( SE ), а другой параллельно ( PE ). Активная сила сократительного элемента исходит из силы, создаваемой актиновыми и миозиновыми поперечными мостиками на уровне саркомера . Он полностью растяжим в неактивном состоянии, но способен укорачиваться при активации. Соединительные ткани ( фасция , эпимизий , перимизий и эндомизий ), которые окружают сократительный элемент, влияют на кривую силы-длины мышцы. Параллельный элемент представляет пассивную силу этих соединительных тканей и имеет мягкотканное механическое поведение. Параллельный элемент отвечает за пассивное поведение мышцы, когда она растянута , даже когда сократительный элемент не активирован. Последовательный элемент представляет сухожилие и внутреннюю эластичность миофиламентов. Он также имеет мягкотканную реакцию и обеспечивает механизм накопления энергии. [2] [3]
Чистая сила-длина характеристики мышцы является комбинацией силы-длины характеристик как активных, так и пассивных элементов. Силы в сократительном элементе, в последовательном элементе и в параллельном элементе, и , соответственно, удовлетворяют
С другой стороны, длина мышц и длины этих элементов удовлетворяют
Во время изометрических сокращений последовательный упругий компонент находится под напряжением и, следовательно, растягивается на конечную величину. Поскольку общая длина мышцы сохраняется постоянной, растяжение последовательного элемента может происходить только при равном укорочении самого сократительного элемента. [2]
Силы в параллельных, последовательных и сократительных элементах определяются как: где — меры деформации для различных элементов, определяемые как: где — длина деформированной мышцы, а — длина деформированной мышцы из-за движения сократительного элемента, обе из уравнения (3). — длина покоя мышцы. можно разделить как . Силовой член, , — это пиковая изометрическая мышечная сила, а функции задаются как:
где — эмпирические константы. Функция из уравнения (4) представляет собой мышечную активацию. Она определяется на основе обычного дифференциального уравнения: где — временные константы, связанные с ростом и спадом мышечной активации, а — минимальная граница, все определяется экспериментально. — нервное возбуждение, которое приводит к сокращению мышцы. [4] [5]
Вязкоупругость
Мышцы представляют вязкоупругость , поэтому вязкий демпфер может быть включен в модель, когда рассматривается динамика критически затухающего сокращения второго порядка . Одной из распространенных моделей для мышечной вязкости является демпфер экспоненциальной формы, где
добавляется к глобальному уравнению модели, где и являются константами. [2]
Смотрите также
Ссылки
- ^ Хилл, А. В. (октябрь 1938 г.). «Теплота сокращения и динамические константы мышц». Proc. R. Soc. Lond. B. 126 ( 843). Лондон: Королевское общество: 136–195. doi : 10.1098/rspb.1938.0050 .
- ^ abcd Fung, Y.-C. (1993). Биомеханика: механические свойства живых тканей . Нью-Йорк: Springer-Verlag. стр. 568. ISBN 0-387-97947-6.
- ^ Мартинс, JAC; Пирес, EB; Сальвадо, R.; Динис, PB (1998). «Численная модель пассивного и активного поведения скелетных мышц». Компьютерные методы в прикладной механике и машиностроении . 151 (3–4). Elsevier: 419–433. Bibcode : 1998CMAME.151..419M. doi : 10.1016/S0045-7825(97)00162-X.
- ^ Панди, Маркус Г.; Заджак, Феликс Э.; Сим, Ынсап; Левин, Уильям С. (1990-01-01). «Оптимальная модель управления для прыжков человека на максимальную высоту». Журнал биомеханики . 23 (12): 1185–1198. doi : 10.1016/0021-9290(90)90376-E . ISSN 0021-9290. PMID 2292598.
- ^ Мартинс, JAC; Пато, MPM; Пирес, EB (2006-09-01). «Конечноэлементная модель скелетных мышц». Виртуальное и физическое прототипирование . 1 (3): 159–170. doi :10.1080/17452750601040626. ISSN 1745-2759. S2CID 137665181.




























![{\displaystyle {\begin{array}{lcr}f^{PE}(\lambda _{f})={\begin{cases}2cA(\lambda _{f}-1)e^{c(\lambda _{f}-1)^{2}},&\lambda _{f}>1\\{\text{0}},&{\text{иначе}}\end{cases}},&(6)\\[4pt]f^{SE}(\lambda ^{ SE},\lambda ^{CE})={\begin{cases}0.1(e^{100\lambda ^{CE}(\lambda ^{SE}-1)}-1),&\lambda ^{SE}\geq 1\\{\text{0}},&{\text{иначе}}\end{cases}},&(7)\\[4pt]f_{L}^{CE}(\lambda ^{CE} )={\begin{cases}-4(\lambda ^{CE}-1)^{2}+1,&0.5\leq \lambda ^{CE}\leq 1.5\\{\text{0}} ,&{\text{иначе}}\end{cases}},&(8)\\[4pt]f_{V}^{CE}({\dot {\lambda }}^{CE})={\ begin{cases}{\text{0}},&{\dot {\lambda }}^{CE}<-10s^{-1}\\-{\frac {1}{\arctan(5)}}\arctan(-0.5{\dot {\lambda }}^{CE})+1,&-10s^{-1}\leq {\dot {\lambda }} ^{CE}\leq 2s^{-1}\\{\frac {\pi }{4\arctan(5)}}+1,&{\dot {\lambda }}^{CE}>2s^{ -1}\end{cases}},&(9)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d6ee32e4a7f6a34f426ad1573796050962f5504)







