система Гильберта
Система формальной дедукции в логике

В логике , а точнее в теории доказательств , система Гильберта , иногда называемая исчислением Гильберта , системой в стиле Гильберта , системой доказательств в стиле Гильберта , дедуктивной системой в стиле Гильберта или системой Гильберта–Аккермана , представляет собой тип формальной системы доказательств , приписываемой Готтлобу Фреге [1] и Дэвиду Гильберту . [2] Эти дедуктивные системы чаще всего изучаются для логики первого порядка , но представляют интерес и для других логик.

Она определяется как дедуктивная система, которая генерирует теоремы из аксиом и правил вывода, [3] [4] [5] особенно если единственным правилом вывода является modus ponens . [6] [7] Каждая система Гильберта является аксиоматической системой , которая используется многими авторами как единственный менее конкретный термин для объявления их систем Гильберта, [8] [9] [10] без упоминания каких-либо более конкретных терминов. В этом контексте «системы Гильберта» противопоставляются естественным системам вывода , [3] в которых не используются никакие аксиомы, а только правила вывода.

В то время как все источники, которые ссылаются на «аксиоматическую» логическую систему доказательства, характеризуют ее просто как логическую систему доказательства с аксиомами, источники, которые используют варианты термина «система Гильберта», иногда определяют ее по-разному, что не будет использоваться в этой статье. Например, Троэльстра определяет «систему Гильберта» как систему с аксиомами и с и как единственными правилами вывода. [11] Конкретный набор аксиом также иногда называют «системой Гильберта», [12] или «исчислением в стиле Гильберта». [13] Иногда «стиль Гильберта» используется для обозначения типа аксиоматической системы, в которой аксиомы даны в схематической форме, [2] как в § Схематическая форма P2 ниже, — но другие источники используют термин «стиль Гильберта» как охватывающий как системы со схематическими аксиомами, так и системы с правилом подстановки, [14] как в этой статье. Использование термина «стиль Гильберта» и подобных ему терминов для описания аксиоматических систем доказательств в логике обусловлено влиянием « Принципов математической логики » Гильберта и Аккермана (1928). [2] → Э {\displaystyle {\rightarrow }E} ∀ я {\displaystyle {\forall }Я}

Большинство вариантов систем Гильберта придерживаются характерного подхода, балансируя между логическими аксиомами и правилами вывода . [1] [15] [16] [17] Системы Гильберта можно охарактеризовать выбором большого количества схем логических аксиом и небольшого набора правил вывода . Системы естественного вывода придерживаются противоположного подхода, включая много правил вывода, но очень мало или вообще не содержат схем аксиом. [3] Наиболее часто изучаемые системы Гильберта имеют либо только одно правило вывода — modus ponens , для пропозициональных логик  , либо два — с обобщением , для обработки также и предикатных логик , — и несколько бесконечных схем аксиом. Системы Гильберта для алетических модальных логик , иногда называемые системами Гильберта-Льюиса, дополнительно требуют правила необходимости. Некоторые системы используют конечный список конкретных формул в качестве аксиом вместо бесконечного набора формул через схемы аксиом, в этом случае требуется правило единой подстановки. [18]

Характерной чертой многих вариантов систем Гильберта является то, что контекст не изменяется ни в одном из их правил вывода, в то время как и естественная дедукция , и секвенциальное исчисление содержат некоторые правила изменения контекста. [19] Таким образом, если кого-то интересует только выводимость тавтологий , а не гипотетические суждения, то можно формализовать систему Гильберта таким образом, что ее правила вывода будут содержать только суждения довольно простой формы. То же самое нельзя сделать с двумя другими системами выводов: [ требуется цитата ] поскольку контекст изменяется в некоторых из их правил вывода, их нельзя формализовать так, чтобы можно было избежать гипотетических суждений — даже если мы хотим использовать их только для доказательства выводимости тавтологий.

Формальные вычеты

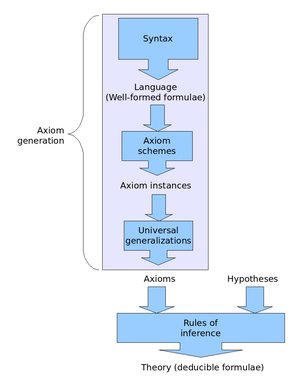
Графическое представление системы вычетов
Графическое представление системы вычетов

В системе Гильберта формальный вывод (или доказательство ) — это конечная последовательность формул, в которой каждая формула является либо аксиомой, либо получена из предыдущих формул с помощью правила вывода. Эти формальные выводы призваны отражать доказательства на естественном языке, хотя они гораздо более подробны.

Предположим, что есть набор формул, рассматриваемых как гипотезы . Например, может быть набором аксиом для теории групп или теории множеств . Обозначение означает, что есть вывод, который заканчивается использованием в качестве аксиом только логических аксиом и элементов . Таким образом, неформально, означает, что доказуемо, предполагая все формулы в . Г {\displaystyle \Гамма} Г {\displaystyle \Гамма} Г ⊢ ϕ {\displaystyle \Гамма \vdash \phi} ϕ {\displaystyle \фи} Г {\displaystyle \Гамма} Г ⊢ ϕ {\displaystyle \Гамма \vdash \phi} ϕ {\displaystyle \фи} Г {\displaystyle \Гамма}

Системы Гильберта характеризуются использованием многочисленных схем логических аксиом . Схема аксиом — это бесконечное множество аксиом, полученных путем подстановки всех формул некоторой формы в определенный шаблон. Множество логических аксиом включает в себя не только аксиомы, полученные из этого шаблона, но и любое обобщение одной из этих аксиом. Обобщение формулы получается путем добавления к формуле нуля или более кванторов всеобщности; например, это обобщение . ∀ у ( ∀ х П х у → П т у ) {\displaystyle \forall y(\forall xPxy\to Pty)} ∀ х П х у → П т у {\displaystyle \forall xPxy\to Pty}

Логика высказываний

Ниже приведены некоторые системы Гильберта, которые использовались в пропозициональной логике . Одна из них, § Схематическая форма P2, также считается системой Фреге .

ФрегеBegriffsschrift

Аксиоматические доказательства использовались в математике со времен знаменитого древнегреческого учебника «Элементы геометрии» Евклида , ок . 300 г. до н. э. Но первая известная полностью формализованная система доказательств, которая тем самым квалифицируется как система Гильберта, восходит к Begriffsschrift Готтлоба Фреге 1879 года . [9] [20] Система Фреге использовала только импликацию и отрицание в качестве связок, [21] и имела шесть аксиом, [20] которые были следующими: [22] [23]

  • Предложение 1: а ⊃ ( б ⊃ а ) {\displaystyle a\supset (b\supset a)}
  • Предложение 2: ( с ⊃ ( б ⊃ а ) ) ⊃ ( ( с ⊃ б ) ⊃ ( с ⊃ а ) ) {\displaystyle (c\supset (b\supset a))\supset ((c\supset b)\supset (c\supset a))}
  • Предложение 8: ( г ⊃ ( б ⊃ а ) ) ⊃ ( б ⊃ ( г ⊃ а ) ) {\displaystyle (d\supset (b\supset a))\supset (b\supset (d\supset a))}
  • Предложение 28: ( б ⊃ а ) ⊃ ( ¬ а ⊃ ¬ б ) {\displaystyle (b\supset a)\supset (\neg a\supset \neg b)}
  • Предложение 31: ¬ ¬ а ⊃ а {\displaystyle \отрицательный \отрицательный а\супсет а}
  • Предложение 41: а ⊃ ¬ ¬ а {\displaystyle a\supset \neg \neg a}

Фреге использовал их вместе с modus ponens и правилом подстановки (которое использовалось, но никогда точно не формулировалось), чтобы получить полную и последовательную аксиоматизацию классической истинностно-функциональной пропозициональной логики. [22]

Лукасевич P2

Ян Лукасевич показал, что в системе Фреге «третья аксиома излишняя, поскольку ее можно вывести из двух предыдущих аксиом, и что последние три аксиомы можно заменить одним предложением ». [23] Что, взятое из польской записи Лукасевича в современную запись, означает . Таким образом, Лукасевичу приписывают [20] эту систему из трех аксиом: С С Н п Н д С д п {\displaystyle CCNpNqCqp} ( ¬ п → ¬ д ) → ( д → п ) {\displaystyle (\отрицательный p\rightarrow \отрицательный q)\rightarrow (q\rightarrow p)}

  • п → ( д → п ) {\displaystyle p\to (q\to p)}
  • ( п → ( д → г ) ) → ( ( п → д ) → ( п → г ) ) {\displaystyle (p\to (q\to r))\to ((p\to q)\to (p\to r))}
  • ( ¬ п → ¬ д ) → ( д → п ) {\displaystyle (\отрицательный p\to \отрицательный q)\to (q\to p)}

Как и система Фреге, эта система использует правило подстановки и использует modus ponens в качестве правила вывода. [20] Точно такую ​​же систему (с явным правилом подстановки) дал Алонзо Чёрч , [24] который назвал её системой P 2, [24] [25] и помог популяризировать её. [25]

Схематическая форма P2

Можно избежать использования правила подстановки, представив аксиомы в схематической форме, используя их для создания бесконечного набора аксиом. Следовательно, используя греческие буквы для представления схем (металогических переменных, которые могут обозначать любые правильно сформированные формулы ), аксиомы задаются как: [9] [25]

  • φ → ( ψ → φ ) {\displaystyle \varphi \to (\psi \to \varphi)}
  • ( φ → ( ψ → χ ) ) → ( ( φ → ψ ) → ( φ → χ ) ) {\displaystyle (\varphi \to (\psi \to \chi))\to ((\varphi \to \psi)\to (\varphi \to \chi))}
  • ( ¬ φ → ¬ ψ ) → ( ψ → φ ) {\displaystyle (\neg \varphi \to \neg \psi) \to (\psi \to \varphi)}

Схематическая версия P 2 приписывается Джону фон Нейману [ 20] и используется в базе данных формальных доказательств Metamath "set.mm". [25] Фактически, сама идея использования схем аксиом для замены правила подстановки приписывается фон Нейману. [26] Схематическая версия P 2 также приписывается Гильберту и названа в этом контексте. [27] ЧАС {\displaystyle {\mathcal {H}}}

Системы для пропозициональной логики, правила вывода которых схематичны, также называются системами Фреге ; как отмечают авторы, которые изначально определили термин «система Фреге» [28] , это фактически исключает собственную систему Фреге, приведенную выше, поскольку она имела аксиомы вместо схем аксиом. [26]

Пример доказательства в P2

В качестве примера ниже приведено доказательство в P 2. Сначала аксиомам даны имена: А → А {\displaystyle A\to A}

(А1) ( п → ( д → п ) ) {\displaystyle (p\to (q\to p))}
(А2) ( ( п → ( д → г ) ) → ( ( п → д ) → ( п → г ) ) ) {\displaystyle ((p\to (q\to r))\to ((p\to q)\to (p\to r)))}
(А3) ( ( ¬ п → ¬ д ) → ( д → п ) ) {\displaystyle ((\отрицательный p\to \отрицательный q)\to (q\to p))}

И доказательство следующее:

  1. А → ( ( Б → А ) → А ) {\displaystyle A\to ((B\to A)\to A)}       (пример (A1))
  2. ( А → ( ( Б → А ) → А ) ) → ( ( А → ( Б → А ) ) → ( А → А ) ) {\displaystyle (A\to ((B\to A)\to A))\to ((A\to (B\to A))\to (A\to A))}       (пример (A2))
  3. ( А → ( Б → А ) ) → ( А → А ) {\displaystyle (A\to (B\to A))\to (A\to A)}       (из (1) и (2) по modus ponens )
  4. А → ( Б → А ) {\displaystyle A\to (B\to A)}       (пример (A1))
  5. А → А {\displaystyle A\to A}       (из (4) и (3) по modus ponens)

Логика предикатов (пример системы)

Существует неограниченное количество аксиоматизаций предикатной логики, поскольку для любой логики существует свобода в выборе аксиом и правил, характеризующих эту логику. Мы описываем здесь систему Гильберта с девятью аксиомами и только правилом modus ponens, которое мы называем аксиоматизацией с одним правилом и которое описывает классическую эквациональную логику. Мы имеем дело с минимальным языком для этой логики, где формулы используют только связки и и только квантор . Позже мы покажем, как систему можно расширить, включив дополнительные логические связки, такие как и , не расширяя класс выводимых формул. ¬ {\displaystyle \lnot} → {\displaystyle \to} ∀ {\displaystyle \forall} ∧ {\displaystyle \земля} ∨ {\displaystyle \лор }

Первые четыре схемы логических аксиом позволяют (вместе с modus ponens) манипулировать логическими связками.

П1. ϕ → ϕ {\ displaystyle \ фи \ к \ фи}
П2. ϕ → ( ψ → ϕ ) {\displaystyle \phi \to \left(\psi \to \phi \right)}
П3. ( ϕ → ( ψ → ξ ) ) → ( ( ϕ → ψ ) → ( ϕ → ξ ) ) {\displaystyle \left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)}
П4. ( ¬ ϕ → ¬ ψ ) → ( ψ → ϕ ) {\displaystyle \left(\lnot \phi \to \lnot \psi \right)\to \left(\psi \to \phi \right)}

Аксиома P1 избыточна, как следует из P3, P2 и modus ponens (см. доказательство). Эти аксиомы описывают классическую пропозициональную логику ; без аксиомы P4 мы получаем позитивную импликационную логику . Минимальная логика достигается либо добавлением вместо нее аксиомы P4m, либо определением как . ¬ ϕ {\displaystyle \lnot \phi} ϕ → ⊥ {\displaystyle \phi \to \bot}

П4м. ( ϕ → ψ ) → ( ( ϕ → ¬ ψ ) → ¬ ϕ ) {\displaystyle \left(\phi \to \psi \right)\to \left(\left(\phi \to \lnot \psi \right)\to \lnot \phi \right)}

Интуиционистская логика достигается путем добавления аксиом P4i и P5i к позитивной импликационной логике или путем добавления аксиомы P5i к минимальной логике. И P4i, и P5i являются теоремами классической пропозициональной логики.

П4и. ( ϕ → ¬ ϕ ) → ¬ ϕ {\displaystyle \left(\phi \to \lnot \phi \right)\to \lnot \phi }
П5и. ¬ ϕ → ( ϕ → ψ ) {\displaystyle \lnot \phi \to \left(\phi \to \psi \right)}

Обратите внимание, что это схемы аксиом, которые представляют бесконечно много конкретных примеров аксиом. Например, P1 может представлять конкретный пример аксиомы или может представлять : это место, где может быть размещена любая формула. Такая переменная, которая варьируется по формулам, называется «схематической переменной». p → p {\displaystyle p\to p} ( p → q ) → ( p → q ) {\displaystyle \left(p\to q\right)\to \left(p\to q\right)} ϕ {\displaystyle \phi }

С помощью второго правила равномерной подстановки (US) мы можем изменить каждую из этих схем аксиом в одну аксиому, заменив каждую схематическую переменную некоторой пропозициональной переменной, которая не упоминается ни в одной аксиоме, чтобы получить то, что мы называем подстановочной аксиоматизацией. Обе формализации имеют переменные, но там, где аксиоматизация с одним правилом имеет схематические переменные, которые находятся вне языка логики, подстановочная аксиоматизация использует пропозициональные переменные, которые выполняют ту же работу, выражая идею переменной, ранжирующейся по формулам с правилом, которое использует подстановку.

НАС. Пусть будет формулой с одним или несколькими экземплярами пропозициональной переменной , и пусть будет другой формулой. Тогда из выведите . ϕ ( p ) {\displaystyle \phi (p)} p {\displaystyle p} ψ {\displaystyle \psi } ϕ ( p ) {\displaystyle \phi (p)} ϕ ( ψ ) {\displaystyle \phi (\psi )}

Следующие три схемы логических аксиом предоставляют способы добавления, манипулирования и удаления универсальных квантификаторов.

Q5. где t может быть заменено на x в ∀ x ( ϕ ) → ϕ [ x := t ] {\displaystyle \forall x\left(\phi \right)\to \phi [x:=t]} ϕ {\displaystyle \,\!\phi }
В6. ∀ x ( ϕ → ψ ) → ( ∀ x ( ϕ ) → ∀ x ( ψ ) ) {\displaystyle \forall x\left(\phi \to \psi \right)\to \left(\forall x\left(\phi \right)\to \forall x\left(\psi \right)\right)}
Q7. где x не является свободным в . ϕ → ∀ x ( ϕ ) {\displaystyle \phi \to \forall x\left(\phi \right)} ϕ {\displaystyle \phi }

Эти три дополнительных правила расширяют пропозициональную систему для аксиоматизации классической предикатной логики . Аналогично, эти три правила расширяют систему для интуиционистской пропозициональной логики (с P1-3 и P4i и P5i) до интуиционистской предикатной логики.

Универсальной квантификации часто придается альтернативная аксиоматизация с использованием дополнительного правила обобщения (см. раздел «Метатеоремы»), в этом случае правила Q6 и Q7 излишни.

Окончательные схемы аксиом необходимы для работы с формулами, содержащими символ равенства.

I8. для каждой переменной x . x = x {\displaystyle x=x}
И9. ( x = y ) → ( ϕ [ z := x ] → ϕ [ z := y ] ) {\displaystyle \left(x=y\right)\to \left(\phi [z:=x]\to \phi [z:=y]\right)}

Консервативные расширения

Обычно в систему Гильберта включают только аксиомы для логических операторов импликации и отрицания в направлении функциональной полноты . Учитывая эти аксиомы, можно сформировать консервативные расширения теоремы о дедукции , которые разрешают использование дополнительных связок. Эти расширения называются консервативными, потому что если формула φ, включающая новые связки, переписывается как логически эквивалентная формула θ, включающая только отрицание, импликацию и универсальную квантификацию, то φ выводима в расширенной системе тогда и только тогда, когда θ выводима в исходной системе. При полном расширении система Гильберта будет больше походить на систему естественной дедукции .

Экзистенциальная квантификация

  • Введение
∀ x ( ϕ → ∃ y ( ϕ [ x := y ] ) ) {\displaystyle \forall x(\phi \to \exists y(\phi [x:=y]))}
  • Устранение
∀ x ( ϕ → ψ ) → ∃ x ( ϕ ) → ψ {\displaystyle \forall x(\phi \to \psi )\to \exists x(\phi )\to \psi } где не является свободной переменной . x {\displaystyle x} ψ {\displaystyle \psi }

Конъюнкция и дизъюнкция

  • Введение и исключение союзов
введение: α → ( β → α ∧ β ) {\displaystyle \alpha \to (\beta \to \alpha \land \beta )}
осталось исключить: α ∧ β → α {\displaystyle \alpha \wedge \beta \to \alpha }
Право на устранение: α ∧ β → β {\displaystyle \alpha \wedge \beta \to \beta }
  • Введение и устранение дизъюнкции
введение слева: α → α ∨ β {\displaystyle \alpha \to \alpha \vee \beta }
введение справа: β → α ∨ β {\displaystyle \beta \to \alpha \vee \beta }
исключение: ( α → γ ) → ( ( β → γ ) → α ∨ β → γ ) {\displaystyle (\alpha \to \gamma )\to ((\beta \to \gamma )\to \alpha \vee \beta \to \gamma )}

Метатеоремы

Поскольку системы Гильберта имеют очень мало правил вывода, обычно доказывают метатеоремы , которые показывают, что дополнительные правила вывода не добавляют дедуктивной силы, в том смысле, что вывод, использующий новые правила вывода, можно преобразовать в вывод, использующий только исходные правила вывода.

Смотрите также

Примечания

  1. ^ ab Máté & Ruzsa 1997:129
  2. ^ abc Смит, Питер (21.02.2013). Введение в теоремы Гёделя. Cambridge University Press. стр. 10. ISBN 978-1-107-02284-3.
  3. ^ abc Restall, Greg (2002-09-11). Введение в субструктурную логику. Routledge. стр.  73–74 . ISBN 978-1-135-11131-1.
  4. ^ Gaifman, Haim (2002). "Дедуктивная система типа Гильберта для сентенциальной логики, полнота и компактность" (PDF) . Columbia . Получено 2024-08-19 .
  5. ^ Бентем, Йохан ван; Гупта, Амитабха; Парих, Рохит (2011-04-02). Доказательство, вычисление и агентство: логика на перепутье. Springer Science & Business Media. стр. 41. ISBN 978-94-007-0080-2.
  6. ^ Бэкон, Эндрю (2023-09-29). Философское введение в логику высшего порядка. Тейлор и Фрэнсис. стр. 424. ISBN 978-1-000-92575-3.
  7. ^ Эйк, Ян ван (26 февраля 1991 г.). Логика в искусственном интеллекте: европейский семинар JELIA '90, Амстердам, Нидерланды, 10–14 сентября 1990 г. Материалы. Springer Science & Business Media. п. 113. ИСБН 978-3-540-53686-4.
  8. ^ Хаак, Сьюзен (1978-07-27). Философия логики. Cambridge University Press. стр. 19. ISBN 978-0-521-29329-7.
  9. ^ abc Bostock, David (1997). Промежуточная логика . Oxford: New York: Clarendon Press; Oxford University Press. стр.  4– 5, 8– 13, 18– 19, 22, 27, 29, 191, 194. ISBN 978-0-19-875141-0.
  10. ^ Лукас, Дж. Р. (2018-10-10). Трактат о времени и пространстве. Routledge. стр. 152. ISBN 978-0-429-68517-0.
  11. ^ Troelstra, AS; Schwichtenberg, H. (2000). Basic Proof Theory. Cambridge Tracts in Theoretical Computer Science (2-е изд.). Кембридж: Cambridge University Press. стр. 51. doi : 10.1017/cbo9781139168717. ISBN 978-0-521-77911-1.
  12. ^ "Введение в логику - Глава 4". intrologic.stanford.edu . Получено 2024-08-16 .
  13. ^ Басс, SR (1998-07-09). Справочник по теории доказательств. Elsevier. С.  552–553 . ISBN 978-0-08-053318-6.
  14. ^ Оно, Хироакира (2019-08-02). Теория доказательств и алгебра в логике. Springer. стр. 5. ISBN 978-981-13-7997-0.
  15. ^ Бэкон, Эндрю (2023-09-29). Философское введение в логику высшего порядка. Тейлор и Фрэнсис. стр. 424. ISBN 978-1-000-92575-3.
  16. ^ Эйк, Ян ван (26 февраля 1991 г.). Логика в искусственном интеллекте: европейский семинар JELIA '90, Амстердам, Нидерланды, 10–14 сентября 1990 г. Материалы. Springer Science & Business Media. п. 113. ИСБН 978-3-540-53686-4.
  17. ^ Troelstra, AS; Schwichtenberg, H. (2000). Basic Proof Theory. Cambridge Tracts in Theoretical Computer Science (2-е изд.). Кембридж: Cambridge University Press. стр. 51. doi : 10.1017/cbo9781139168717. ISBN 978-0-521-77911-1.
  18. ^ Оно, Хироакира (2019-08-02). Теория доказательств и алгебра в логике. Springer. стр. 5. ISBN 978-981-13-7997-0.
  19. ^ Габбай, Дов М.; Гюнтнер, Франц (2013-03-14). Справочник по философской логике. Springer Science & Business Media. стр. 201. ISBN 978-94-017-0458-8.
  20. ^ abcde Smullyan, Raymond M. (2014-07-23). ​​Руководство для начинающих по математической логике. Courier Corporation. С.  102– 103. ISBN 978-0-486-49237-7.
  21. ^ Фрэнкс, Кертис (2023), «Пропозициональная логика», в Zalta, Edward N.; Nodelman, Uri (ред.), The Stanford Encyclopedia of Philosophy (ред. осень 2023 г.), Metaphysics Research Lab, Stanford University , получено 22.03.2024
  22. ^ ab Мендельсон, Ричард Л. (2005-01-10). Философия Готтлоба Фреге. Cambridge University Press. стр. 185. ISBN 978-1-139-44403-3.
  23. ^ Аб Лукасевич, Январь (1970). Ян Лукасевич: Избранные произведения. Северная Голландия. п. 136.
  24. ^ ab Church, Alonzo (1996). Введение в математическую логику. Princeton University Press. стр. 119. ISBN 978-0-691-02906-1.
  25. ^ abcd "Proof Explorer - Домашняя страница - Metamath". us.metamath.org . Получено 2024-07-02 .
  26. ^ ab Кук, Стивен А.; Рекхоу, Роберт А. (1979). «Относительная эффективность систем пропозициональных доказательств». Журнал символической логики . 44 (1): 39. doi :10.2307/2273702. ISSN  0022-4812. JSTOR  2273702.
  27. ^ Валицкий, Михал (2017). Введение в математическую логику (Расширенное издание). Нью-Джерси: World Scientific. стр. 126. ISBN 978-981-4719-95-7.
  28. ^ Пудлак, Павел; Бусс, Сэмюэл Р. (1995). «Как лгать, не будучи (легко) осужденным, и длина доказательств в исчислении высказываний». В Pacholski, Leszek; Tiuryn, Jerzy (ред.). Computer Science Logic . Lecture Notes in Computer Science. Vol. 933. Berlin, Heidelberg: Springer. p. 152. doi :10.1007/BFb0022253. ISBN 978-3-540-49404-1.

Ссылки

  • Карри, Хаскелл Б.; Роберт Фейс (1958). Комбинаторная логика. Т. I. Т. 1. Амстердам: Северная Голландия.
  • Монк, Дж. Дональд (1976). Математическая логика . Тексты для выпускников по математике. Берлин, Нью-Йорк: Springer-Verlag . ISBN 978-0-387-90170-1.
  • Ружа, Имре; Мате, Андраш (1997). Bevezetés - современная логикаба (на венгерском языке). Будапешт: Осирис Киадо.
  • Тарский, Альфред (1990). Bizonyítás é igazság (на венгерском языке). Будапешт: Гондолат.Это венгерский перевод избранных статей Альфреда Тарского по семантической теории истины .
  • Давид Гильберт (1927) «Основания математики», перевод Стефана Бауэра-Менглерберга и Дагфинна Фёллесдаля (стр. 464–479). в:
    • ван Хейеноорт, Жан (1967). От Фреге до Гёделя: Учебник по математической логике, 1879–1931 (3-е издание, 1976 г.). Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN 0-674-32449-8.
    • В своей работе 1927 года «Основания» (стр. 367–392) Гильберт представил свои 17 аксиом — аксиомы импликации № 1–4, аксиомы о & и V № 5–10, аксиомы отрицания № 11–12, свою логическую ε-аксиому № 13, аксиомы равенства № 14–15 и аксиомы чисел № 16–17 — вместе с другими необходимыми элементами своей формалистской «теории доказательств», например, аксиомами индукции, аксиомами рекурсии и т. д.; он также предлагает энергичную защиту от интуиционизма Л. Э. Брауэра. См. также комментарии и опровержения Германа Вейля (1927) (стр. 480–484), приложение Пола Бернея (1927) к лекции Гильберта (стр. 485–489) и ответ Луицена Эгбертуса Яна Брауэра (1927) (стр. 490–495).
  • Клини, Стивен Коул (1952). Введение в метаматематику (10-е издание с исправлениями 1971 г.). Амстердам, Нью-Йорк: North Holland Publishing Company. ISBN 0-7204-2103-9.
    • См., в частности, главу IV «Формальная система» (стр. 69–85), в которой Клини представляет подразделы §16 «Формальные символы», §17 «Правила формирования», §18 «Свободные и связанные переменные (включая подстановку)», §19 «Правила преобразования» (например, modus ponens) — и из них он представляет 21 «постулат» — 18 аксиом и 3 отношения «непосредственного следствия», разделенные следующим образом: постулаты для исчисления высказываний № 1–8, дополнительные постулаты для исчисления предикатов № 9–12 и дополнительные постулаты для теории чисел № 13–21.
  • Гайфман, Хаим. «Дедуктивная система типа Гильберта для сентенциальной логики, полнота и компактность» (PDF) .
  • Фармер, В. М. «Пропозициональная логика» (PDF) .В нем описывается (среди прочего) конкретная система доказательств в стиле Гильберта (ограниченная исчислением высказываний ).
Retrieved from "https://en.wikipedia.org/w/index.php?title=Hilbert_system&oldid=1257978821"