Закон Гесса
Наблюдение, что общее изменение энтальпии химической реакции не зависит от предпринятых шагов
Представление закона Гесса (где H представляет энтальпию)

Закон Гесса о постоянном суммировании тепла , также известный как закон Гесса , представляет собой соотношение в физической химии и термодинамике [1], названное в честь Жермена Гесса , русского химика и врача швейцарского происхождения , который опубликовал его в 1840 году. Закон гласит, что общее изменение энтальпии в течение всего хода химической реакции не зависит от последовательности выполненных шагов. [2] [3]

Закон Гесса теперь понимается как выражение того факта, что энтальпия химического процесса не зависит от пути, пройденного от начального до конечного состояния (т. е. энтальпия является функцией состояния ). Согласно первому закону термодинамики , изменение энтальпии в системе из-за реакции при постоянном давлении равно поглощенному теплу (или отрицательному значению выделенного тепла), которое может быть определено калориметрией для многих реакций. Значения обычно указываются для реакций с одинаковыми начальными и конечными температурами и давлениями (при этом условия могут меняться в ходе реакций). Закон Гесса можно использовать для определения общей энергии, необходимой для химической реакции, которую можно разделить на синтетические этапы, которые по отдельности легче охарактеризовать. Это позволяет составить стандартные энтальпии образования , которые можно использовать для прогнозирования изменения энтальпии в сложном синтезе.

Теория

Закон Гесса гласит, что изменение энтальпии в химической реакции одинаково независимо от того, происходит ли реакция в один этап или в несколько этапов, при условии, что начальное и конечное состояние реагентов и продуктов одинаковы. Энтальпия является экстенсивным свойством , то есть ее значение пропорционально размеру системы. [4] Из-за этого изменение энтальпии пропорционально числу молей, участвующих в данной реакции.

Другими словами, если химическое изменение происходит несколькими различными путями, общее изменение энтальпии одинаково, независимо от пути, по которому происходит химическое изменение (при условии, что начальное и конечное состояние одинаковы). Если бы это было не так, то можно было бы нарушить первый закон термодинамики .

Закон Гесса позволяет рассчитать изменение энтальпии (Δ H ) для реакции, даже если его невозможно измерить напрямую. Это достигается путем выполнения основных алгебраических операций на основе химических уравнений реакций с использованием ранее определенных значений энтальпий образования.

Объединение химических уравнений приводит к чистому или общему уравнению. Если изменения энтальпии известны для всех уравнений в последовательности, их сумма будет изменением энтальпии для чистого уравнения. Если чистое изменение энтальпии отрицательно ( ), реакция экзотермическая и, скорее всего, будет спонтанной ; положительные значения Δ H соответствуют эндотермическим реакциям. ( Энтропия также играет важную роль в определении спонтанности, поскольку некоторые реакции с положительным изменением энтальпии тем не менее являются спонтанными из-за увеличения энтропии в реакционной системе.) Δ ЧАС сеть < 0 {\displaystyle \Delta H_{\text{net}}<0}

Использование энтальпий образования

Закон Гесса гласит, что изменения энтальпии аддитивны. Таким образом, значение стандартной энтальпии реакции можно рассчитать из стандартных энтальпий образования продуктов и реагентов следующим образом:

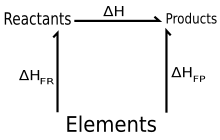
Δ ЧАС реакция ⊖ = ∑ я а я Δ ф ЧАС п г о г ты с т с ⊖ − ∑ я б я Δ ф ЧАС г е а с т а н т с ⊖ {\displaystyle \Delta H_{\text{реакция}}^{\ominus }=\sum _{i}a_{i}\Delta _{\text{f}}H_{продукты}^{\ominus }-\sum _{i}b_{i}\Delta _{\text{f}}H_{реагенты}^{\ominus }}

Здесь первая сумма по всем продуктам, а вторая по всем реагентам, и являются стехиометрическими коэффициентами продуктов и реагентов соответственно, и являются стандартными энтальпиями образования продуктов и реагентов соответственно, а верхний индекс o указывает на стандартные значения состояния. Это можно рассматривать как сумму двух (реальных или фиктивных) реакций: а я {\displaystyle a_{i}} б я {\displaystyle b_{i}} Δ ф ЧАС п г о г ты с т с ⊖ {\displaystyle \Delta _{\text{f}}H_{products}^{\ominus }} Δ ф ЧАС г е а с т а н т с ⊖ {\displaystyle \Delta _{\text{f}}H_{реагенты}^{\ominus }}

Реагенты → Элементы (в их стандартных состояниях)
Δ ЧАС РЕ ⊖ = − ∑ я б я Δ ф ЧАС г е а с т а н т с ⊖ {\displaystyle \Delta H_{\text{RE}}^{\ominus }=-\sum _{i}b_{i}\Delta _{\text{f}}H_{реагенты}^{\ominus }}

и Элементы → Продукты

Δ ЧАС ЭП ⊖ = ∑ я а я Δ ф ЧАС п г о г ты с т с ⊖ {\displaystyle \Delta H_{\text{EP}}^{\ominus }=\sum _{i}a_{i}\Delta _{\text{f}}H_{products}^{\ominus }}

Примеры

  1. Данный:
    1. C графит + O 2 → CO 2 ( г ) ( Δ H = −393,5 кДж/моль) (прямая ступень)
    2. C графит + 1/2 O 2 → CO( г ) (Δ H = -110,5 кДж/моль)
    3. CO( г ​​) +1/2 O 2 → CO 2 ( г ) (Δ H = -283,0 кДж/моль)

    Реакция (а) представляет собой сумму реакций (б) и (в), для которых общая Δ H = −393,5 кДж/моль, что равно Δ H в (а).

  2. Данный:
    • B2O3 ( т ) + 3H2O ( г ) → 3O2 ( г ) + B2H6 ( г ) (ΔH = 2035 кДж / моль )
    • H 2 O( л ) → H 2 O( г ) (Δ H = 44 кДж/моль)
    • ЧАС 2 ( г ) + 1/2 О 2 ( г ) → ЧАС 2 О( л ) (Δ Н = -286 кДж/моль)
    • 2B( т ) + 3H 2 ( г ) → B 2 H 6 ( г ) (Δ H = 36 кДж/моль)
    Найдите Δ f H :
    • 2B( т ) + 3/2 O2 ( г ) → B2O3 ( т )
    После умножения уравнений (и их изменений энтальпии) на соответствующие коэффициенты и изменения направления при необходимости получаем:
    • B2H6 ( г ) + 3O2 ( г ) → B2O3 ( т ) + 3H2O ( г ) ( ΔH = 2035 × (−1) = −2035 кДж/моль )
    • 3H 2 O( г ) → 3H 2 O( ж ) (Δ H = 44 × (−3) = −132 кДж/моль)
    • 3H 2 O( ж ) → 3H 2 ( г ) + (3/2) O 2 ( г ) (Δ H = −286 × (−3) = 858 кДж/моль)
    • 2B( т ) + 3H 2 ( г ) → B 2 H 6 ( г ) (Δ H = 36 кДж/моль)
    Сложив эти уравнения и сократив общие члены с обеих сторон, получим
    • 2B( т ) + 3/2 O 2 ( г ) → B 2 O 3 ( т ) (Δ H = −1273 кДж/моль)

Расширение свободной энергии и энтропии

Концепции закона Гесса можно расширить, включив изменения энтропии и свободной энергии Гиббса , поскольку они также являются функциями состояния . Термодинамический цикл Бордвелла является примером такого расширения, которое использует преимущества легко измеряемых равновесий и окислительно-восстановительных потенциалов для определения экспериментально недоступных значений свободной энергии Гиббса . Объединение значений Δ G o из термодинамических циклов Бордвелла и значений Δ H o, найденных с помощью закона Гесса, может быть полезным для определения значений энтропии, которые не были измерены напрямую и, следовательно, должны быть рассчитаны с помощью альтернативных путей.

Для бесплатной энергии:

Δ Г реакция ⊖ = ∑ ν п Δ Г ф ( п ) ⊖ − ∑ ν г Δ Г ф ( г ) ⊖ . {\displaystyle \Delta G_{\text{reaction}}^{\ominus }=\sum \nu _{\text{p}}\Delta G_{\mathrm {f} \,({\text{p}} )}^{\ominus }-\sum \nu _{\text{r}}\Delta G_{\mathrm {f} \,({\text{r}})}^{\ominus }.}

Для энтропии ситуация немного иная. Поскольку энтропию можно измерить как абсолютное значение, а не относительно значений элементов в их исходных состояниях (как в случае с Δ H o и Δ G o ), нет необходимости использовать энтропию образования; просто используются абсолютные энтропии для продуктов и реагентов:

Δ С реакция ⊖ = ∑ ν п С ( п ) ⊖ − ∑ ν г С ( г ) ⊖ . {\displaystyle \Delta S_{\text{реакция}}^{\ominus }=\sum \nu _{\text{p}}S_{({\text{p}})}^{\ominus }-\sum \nu _{\text{r}}S_{({\text{r}})}^{\ominus }.}

Приложения

Закон Гесса полезен при определении энтальпий следующих веществ: [2]

  1. Теплоты образования нестабильных промежуточных соединений, таких как CO (г) и NO (г) .
  2. Тепловые изменения при фазовых переходах и аллотропных переходах.
  3. Энергии решетки ионных веществ путем построения циклов Борна-Габера, если известно сродство к электрону для образования аниона, или
  4. Сродство к электронам с использованием цикла Борна-Габера с теоретической энергией решетки .

Смотрите также

Ссылки

  1. ^ "5.6: Закон Гесса". Chemistry LibreTexts . 2014-11-18 . Получено 2024-11-09 .
  2. ^ ab Mannam Krishnamurthy; Subba Rao Naidu (2012). "7". В Lokeswara Gupta (ред.). Химия для ISEET - Том 1, Часть A (ред. 2012 г.). Хайдарабад, Индия : Varsity Education Management Limited. стр. 244.
  3. ^ "Закон Гесса - Сохранение энергии". Университет Ватерлоо. Архивировано из оригинала 9 января 2015 года . Получено 12 января 2014 года .
  4. ^ Энгель, Томас; Рид, Филип (2006). Физическая химия . Пирсон / Бенджамин Каммингс. стр. 6. ISBN 0-8053-3842-XПеременная , пропорциональная размеру системы, называется экстенсивной переменной.
  • Чакрабарти, ДК (2001). Введение в физическую химию . Мумбаи: Alpha Science. стр.  34–37 . ISBN 1-84265-059-9.

Дальнейшее чтение

  • Лестер, Генри М. (1951). «Жермен Анри Гесс и основы термохимии». Журнал химического образования . 28 (11): 581– 583. Bibcode : 1951JChEd..28..581L. doi : 10.1021/ed028p581.
  • Статья Гесса (1840), на которой основан его закон (на сайте ChemTeam)
  • эксперимент по закону Гесса Архивировано 2016-03-03 на Wayback Machine
Взято с "https://en.wikipedia.org/w/index.php?title=Hess%27s_law&oldid=1258211143"