Контур Ганкеля
Контурный путь Ганкеля, пройденный в положительном направлении.
Это версия контура Ганкеля, которая представляет собой просто линейное зеркальное отображение относительно действительной оси.

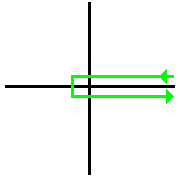
В математике контур Ганкеля — это путь в комплексной плоскости , который простирается от (+∞,δ) вокруг начала координат против часовой стрелки и обратно до (+∞,−δ), где δ — произвольно малое положительное число. Таким образом, контур остается произвольно близким к действительной оси , но не пересекает действительную ось, за исключением отрицательных значений x . Контур Ганкеля также может быть представлен путем, который имеет зеркальные отражения чуть выше и ниже действительной оси, соединенным с окружностью радиуса ε с центром в начале координат, где ε — произвольно малое число. Говорят, что две линейные части контура находятся на расстоянии δ от действительной оси. Таким образом, общее расстояние между линейными частями контура равно 2δ. [1] Контур проходится в положительно ориентированном смысле, что означает, что окружность вокруг начала координат проходится против часовой стрелки.

Использование контуров Ганкеля является одним из методов контурного интегрирования . Этот тип пути для контурных интегралов был впервые использован Германом Ганкелем в его исследованиях гамма -функции .

Контур Ганкеля используется для вычисления интегралов, таких как гамма-функция, дзета-функция Римана и другие функции Ганкеля (которые являются функциями Бесселя третьего рода). [1] [2]

Приложения

Контур Ганкеля и гамма-функция

Контур Ганкеля полезен для выражения и решения гамма-функции в комплексной t -плоскости. Гамма-функция может быть определена для любого комплексного значения в плоскости, если мы вычислим интеграл вдоль контура Ганкеля. Контур Ганкеля особенно полезен для выражения гамма-функции для любого комплексного значения, поскольку конечные точки контура исчезают, и, таким образом, позволяет удовлетворить фундаментальному свойству гамма-функции, которое гласит . [2] Г ( з + 1 ) = з Г ( з ) {\ displaystyle \ Gamma (z + 1) = z \ Gamma (z)}

Вывод контурного интегрального выражения гамма-функции

Контур Ганкеля можно использовать для вывода выражения для гамма-функции [2] на основе фундаментального свойства . Предположим анзац в форме , где — контур Ганкеля. Г ( з + 1 ) = з Г ( з ) {\ displaystyle \ Gamma (z + 1) = z \ Gamma (z)} Г ( з ) = ∫ С ф ( т ) т з − 1 г т {\displaystyle \Гамма (z)=\int _{C}f(t)t^{z-1}dt} С {\displaystyle С}

Подставляя этот анзац в фундаментальное свойство и интегрируя по частям в правой части, получаем ∫ С ф ( т ) т з г т = [ т з ф ( т ) ] − ∫ С т з ф ′ ( т ) г т . {\displaystyle \int _{C}f(t)t^{z}dt=[t^{z}f(t)]-\int _{C}t^{z}f'(t)dt.}

Таким образом, предполагая, что затухает достаточно быстро, так что исчезает в конечных точках контура Ганкеля, ф ( т ) {\displaystyle f(t)} т з ф ( т ) {\displaystyle t^{z}f(t)} ∫ С т з ( ф ( т ) + ф ′ ( т ) ) г т = 0 ⟹ ф ( т ) + ф ′ ( т ) = 0. {\displaystyle \int _{C}t^{z}(f(t)+f'(t))dt=0\implies f(t)+f'(t)=0.}

Решение этого дифференциального уравнения : В то время как является константой относительно , ​​тем не менее может быть функцией . Подстановка в исходный интеграл дает , где знак минус в учитывается путем включения множителя в определение . ф ( т ) = А е − т . {\displaystyle f(t)=Ae^{-t}.} А {\displaystyle А} т {\displaystyle т} А {\displaystyle А} з {\displaystyle z} ф ( т ) {\displaystyle f(t)} Г ( з ) = А ( з ) ∫ С е − т ( − т ) з − 1 г т , {\displaystyle \Гамма (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt,} ( − т ) з − 1 {\displaystyle (-t)^{z-1}} ( − 1 ) з − 1 {\displaystyle (-1)^{z-1}} А ( з ) {\displaystyle A(z)}

Интегрируя по контуру Ганкеля, выражение контурного интеграла гамма-функции становится [ необходимо разъяснение ] . [2] Г ( з ) = я 2 грех ⁡ π з ∫ С е − т ( − т ) з − 1 г т {\displaystyle \Gamma (z)={\frac {i}{2\sin {\pi z}}} \int _{C}e^{-t}(-t)^{z-1}dt}

Ссылки

  1. ^ ab Krantz, Steven G. (Steven George), 1951- (1999). Справочник по комплексным переменным . Бостон, Массачусетс: Birkhäuser. ISBN 0-8176-4011-8. OCLC  40964730.{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )
  2. ^ abcd Моретти, Джино (1964). Функции комплексной переменной . Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. стр.  179–184 . LCCN  64012240.

Дальнейшее чтение

  • Шмельцер, Томас; Трефетен, Ллойд Н. (2007-01). «Вычисление гамма-функции с использованием контурных интегралов и рациональных аппроксимаций». Журнал SIAM по численному анализу. 45 (2): 558–571. doi :10.1137/050646342. ISSN  0036-1429.
  • Хью Л. Монтгомери ; Роберт К. Воган (2007). Мультипликативная теория чисел I. Классическая теория . Кембриджские трактаты по высшей математике. 97. стр. 515. ISBN 0-521-84903-9 . 
  • http://mathworld.wolfram.com/HankelContour.html
  • Цифровая библиотека математических функций NIST: Гамма-функция: Интегральное представление


Взято с "https://en.wikipedia.org/w/index.php?title=Hankel_contour&oldid=1251562754"