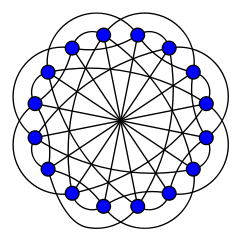
Граф Клебша
Один из двух различных регулярных графов с 16 вершинами
Граф Клебша
Назван в честьАльфред Клебш
Вершины16
Края40
Радиус2
Диаметр2
Обхват4
Автоморфизмы1920
Хроматическое число4 [1]
Хроматический индекс5
Толщина книги4
Номер очереди3
ХарактеристикиСильно регулярный
гамильтонов
граф Кэли
, транзитивный по вершинам, транзитивный
по рёбрам,
транзитивный по расстоянию .
Таблица графиков и параметров

В математической области теории графов граф Клебша является одним из двух дополнительных графов на 16 вершинах, 5- регулярным графом с 40 ребрами и 10-регулярным графом с 80 ребрами. Граф с 80 ребрами является графом куба размерности 5, удвоенным пополам ; он был назван графом Клебша по имени Зайделя (1968) [2] из-за его связи с конфигурацией из 16 линий на поверхности четвертой степени, открытой в 1868 году немецким математиком Альфредом Клебшем . Вариант с 40 ребрами является графом сложенного куба размерности 5 ; он также известен как граф Гринвуда–Глисона в честь работы Роберта Э. Гринвуда и Эндрю М. Глисона  (1955), которые использовали его для оценки числа Рамсея R (3,3,3) = 17. [3] [4] [5]

Строительство

Граф сложенного куба размерности 5 (5-регулярный граф Клебша) может быть построен путем добавления ребер между противоположными парами вершин в 4-мерном гиперкубе. (В n -мерном гиперкубе пара вершин является противоположной, если кратчайший путь между ними имеет n ребер.) В качестве альтернативы его можно сформировать из 5-мерного гиперкуба путем отождествления (или сжатия) каждой противоположной пары вершин.

Другая конструкция, приводящая к тому же графу, заключается в создании вершины для каждого элемента конечного поля GF(16) и соединении двух вершин ребром всякий раз, когда разность между соответствующими двумя элементами поля представляет собой идеальный куб . [6]

Граф куба размерности 5, разделенный пополам (10-регулярный граф Клебша), является дополнением 5-регулярного графа. Он также может быть построен из вершин 5-мерного гиперкуба путем соединения пар вершин, расстояние Хэмминга которых равно ровно двум. Эта конструкция является примером конструкции графов Франкла–Рёдля . Она создает два подмножества из 16 вершин, которые не связаны друг с другом; оба этих полуквадрата гиперкуба изоморфны 10-регулярному графу Клебша. Две копии 5-регулярного графа Клебша могут быть получены таким же образом из 5-мерного гиперкуба путем соединения пар вершин, расстояние Хэмминга которых равно ровно четырем.

Характеристики

5-регулярный граф Клебша является сильно регулярным графом степени 5 с параметрами . [7] [8] Его дополнение, 10-регулярный граф Клебша, поэтому также является сильно регулярным графом, [1] [4] с параметрами . ( в , к , λ , μ ) = ( 16 , 5 , 0 , 2 ) {\displaystyle (v,k,\lambda,\mu)=(16,5,0,2)} ( 16 , 10 , 6 , 6 ) {\displaystyle (16,10,6,6)}

5-регулярный граф Клебша является гамильтоновым , непланарным и неэйлеровым . Он также является как 5- вершинно-связным , так и 5- рёберно-связным . Подграф, который индуцируется десятью не-соседями любой вершины в этом графе, образует изоморфную копию графа Петерсена .

Он имеет толщину книги 4 и номер очереди 3. [9]

K 16 3-цветный как три графа Клебша.

Ребра полного графа K 16 могут быть разделены на три непересекающиеся копии 5-регулярного графа Клебша. Поскольку граф Клебша является графом без треугольников , это показывает, что существует трехцветная раскраска ребер K 16 без треугольников ; то есть, что число Рамсея R (3,3,3), описывающее минимальное количество вершин в полном графе без трехцветной раскраски, равно по крайней мере 17. Гринвуд и Глисон (1955) использовали эту конструкцию как часть своего доказательства того, что R (3,3,3) = 17. [5] [10]

5-регулярный граф Клебша может быть раскрашен четырьмя цветами, но не тремя: его наибольшее независимое множество имеет пять вершин, недостаточно для разбиения графа на три независимых цветовых класса. Он содержит в качестве индуцированного подграфа граф Грётша , наименьший свободный от треугольников четырехцветный граф, и каждый четырехцветный индуцированный подграф графа Клебша является суперграфом графа Грётша. Более строго, каждый свободный от треугольников четырехцветный граф без индуцированного пути длины шесть или более является индуцированным подграфом графа Клебша и индуцированным суперграфом графа Грётша. [11]

5-регулярный граф Клебша — это граф Келлера размерности два, часть семейства графов, используемых для нахождения разбиений многомерных евклидовых пространств на гиперкубы, никакие два из которых не пересекаются лицом к лицу.

5-регулярный граф Клебша может быть вложен как регулярная карта в ориентируемое многообразие рода 5, образуя пятиугольные грани; и в неориентируемую поверхность рода 6, образуя четырехугольные грани.

Алгебраические свойства

Характеристический многочлен 5-регулярного графа Клебша равен . Поскольку этот многочлен может быть полностью разложен на линейные множители с целыми коэффициентами, граф Клебша является целочисленным графом : его спектр состоит исключительно из целых чисел. [4] Граф Клебша является единственным графом с этим характеристическим многочленом, что делает его графом, определяемым его спектром. ( х + 3 ) 5 ( х − 1 ) 10 ( х − 5 ) {\displaystyle (x+3)^{5}(x-1)^{10}(x-5)}

5-регулярный граф Клебша является графом Кэли с группой автоморфизмов порядка 1920, изоморфной группе Коксетера . Как граф Кэли, его группа автоморфизмов действует транзитивно на его вершинах, делая его вершинно транзитивным . Фактически, он является дуго-транзитивным , следовательно, реберно-транзитивным и дистанционно-транзитивным . Он также является связно-однородным , что означает, что любой изоморфизм между двумя связными индуцированными подграфами может быть расширен до автоморфизма всего графа. Д 5 {\displaystyle D_{5}}

Ссылки

  1. ^ ab Weisstein, Eric W. "Clebsch Graph". Из MathWorld—A Wolfram Web Resource . Получено 2009-08-13 .
  2. ^ JJ Seidel, Сильно регулярные графы с матрицей смежности (−1,1,0) , имеющей собственное значение 3, Lin. Alg. Appl. 1 (1968) 281-298.
  3. ^ Клебш, А. (1868), "Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen", Journal für die reine und angewandte Mathematik , 69 : 142–184.
  4. ^ abc "The Clebsch Graph on Bill Cherowitzo's home page" (PDF) . Архивировано из оригинала (PDF) 2013-10-29 . Получено 2011-05-21 .
  5. ^ ab Гринвуд, RE; Глисон, AM (1955), "Комбинаторные отношения и хроматические графы", Канадский журнал математики , 7 : 1–7, doi : 10.4153/CJM-1955-001-4 , MR  0067467.
  6. ^ Де Клерк, Франк (1997). «Конструкции и характеристики (полу)частичных геометрий». Летняя школа по конечным геометриям. стр. 6.
  7. ^ Godsil, CD (1995). "Problems in algebraic combinatorics" (PDF) . Electronic Journal of Combinatorics . 2 : 3. doi :10.37236/1224 . Получено 13 августа 2009 г.
  8. ^ Питер Дж. Кэмерон Сильно регулярные графы на DesignTheory.org, 2001
  9. ^ Джессика Вольц, Проектирование линейных макетов с помощью SAT . Магистерская работа, Тюбингенский университет, 2018 г.
  10. ^ Сан, Хьюго С.; Коэн, М.Э. (1984), «Простое доказательство оценки Гринвуда–Глисона числа Рамсея R(3,3,3)» (PDF) , The Fibonacci Quarterly , 22 (3): 235–238, MR  0765316.
  11. ^ Рандерат, Берт; Ширмейер, Инго; Тьюс, Майке (2002), «Трехцветность и запрещённые подграфы. II. Полиномиальные алгоритмы», Дискретная математика , 251 (1–3): 137–153, doi : 10.1016/S0012-365X(01)00335-1 , MR  1904597.
Взято с "https://en.wikipedia.org/w/index.php?title=Clebsch_graph&oldid=1189621022"