Экспоненциальная функция

Экспоненциальный
График показательной функции
Общая информация
Общее определение	${\displaystyle \exp z=e^{z}}$
Домен, кодомен и изображение
Домен	${\displaystyle \mathbb {C} }$
Изображение	${\displaystyle {\begin{cases}(0,\infty )&{\text{for }}z\in \mathbb {R} \\\mathbb {C} \setminus \{0\}&{\text{for }}z\in \mathbb {C} \end{cases}}}$
Конкретные ценности
На нуле	1
Значение 1	е
Особые черты
Фиксированная точка	− W n (−1) для${\displaystyle n\in \mathbb {Z} }$
Связанные функции
Взаимный	${\displaystyle \exp(-z)}$
Обратный	Натуральный логарифм , Комплексный логарифм
Производный	${\displaystyle \exp '\!z=\exp z}$
Первообразный	${\displaystyle \int \exp z\,dz=\exp z+C}$
Определение серии
ряд Тейлора	${\displaystyle \exp z=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}}$

В математике показательная функция — это уникальная действительная функция , которая отображает ноль в единицу и имеет производную, равную ее значению. Показательная функция переменной ⁠ ⁠${\displaystyle x}$ обозначается ⁠ ⁠${\displaystyle \exp x}$ или ⁠ ⁠${\displaystyle e^{x}}$ , причем эти два обозначения используются взаимозаменяемо. Она называется показательной, потому что ее аргумент можно рассматривать как показатель степени , в которую возводится постоянное число e ≈ 2,718 , основание. Существует несколько других определений показательной функции, которые все эквивалентны, хотя и имеют совершенно разную природу.

Экспоненциальная функция преобразует суммы в произведения: она отображает аддитивное тождество 0 в мультипликативное тождество 1 , а экспонента суммы равна произведению отдельных экспонент, ⁠ ⁠${\displaystyle \exp(x+y)=\exp x\cdot \exp y}$ . Ее обратная функция , натуральный логарифм , ⁠ ⁠${\displaystyle \ln }$ или ⁠ ⁠${\displaystyle \log }$ , преобразует произведения в суммы: ⁠ ⁠${\displaystyle \ln(x\cdot y)=\ln x+\ln y}$ .

Экспоненциальную функцию иногда называют натуральной экспоненциальной функцией , что соответствует названию натуральный логарифм , для отличия ее от некоторых других функций, которые также обычно называют экспоненциальными функциями . Эти функции включают функции формы ⁠ ⁠${\displaystyle f(x)=b^{x}}$ , которая является возведением в степень с фиксированным основанием ⁠ ⁠${\displaystyle b}$ . В более общем смысле, и особенно в приложениях, функции общего вида ⁠ ⁠${\displaystyle f(x)=ab^{x}}$ также называются экспоненциальными функциями. Они растут или затухают экспоненциально, поскольку величина, которая ⁠ ⁠${\displaystyle f(x)}$ изменяется при ⁠ ⁠${\displaystyle x}$ увеличении, пропорциональна текущему значению ⁠ ⁠${\displaystyle f(x)}$ .

Экспоненциальную функцию можно обобщить, чтобы она принимала комплексные числа в качестве аргументов. Это выявляет связи между умножением комплексных чисел, вращениями в комплексной плоскости и тригонометрией . Формула Эйлера ⁠ ⁠${\displaystyle \exp i\theta =\cos \theta +i\sin \theta }$ выражает и суммирует эти связи.

Экспоненциальную функцию можно еще больше обобщить, чтобы она принимала другие типы аргументов, такие как матрицы и элементы алгебр Ли .

График имеет восходящий наклон и растет быстрее, чем любая степень ⁠ ⁠ . ^[1] График всегда лежит выше оси x , но становится произвольно близким к ней для больших отрицательных x ; таким образом, ось x является горизонтальной асимптотой . Уравнение означает, что наклон касательной к графику в каждой точке равен ее высоте (ее координате y ) в этой точке .${\displaystyle y=e^{x}}$${\displaystyle x}$${\displaystyle {\tfrac {d}{dx}}e^{x}=e^{x}}$

Существует несколько эквивалентных определений показательной функции, хотя и весьма различных по своей природе.

Одно из самых простых определений: экспоненциальная функция — это единственная дифференцируемая функция , которая равна своей производной и принимает значение 1 для значения 0 своей переменной.

Это «концептуальное» определение требует доказательства единственности и доказательства существования, но оно позволяет легко вывести основные свойства экспоненциальной функции.

Уникальность: Если ⁠ ⁠${\displaystyle f(x)}$ и ⁠ ⁠${\displaystyle g(x)}$ — две функции, удовлетворяющие приведенному выше определению, то производная ⁠ ⁠${\displaystyle f/g}$ везде равна нулю из-за правила частного . Отсюда следует, что ⁠ ⁠${\displaystyle f/g}$ — константа; эта константа равна 1, поскольку ⁠ ⁠${\displaystyle f(0)=g(0)=1}$ .

Экспоненциальная функция является обратной функцией натурального логарифма . Теорема об обратной функции подразумевает, что натуральный логарифм имеет обратную функцию, которая удовлетворяет приведенному выше определению. Это первое доказательство существования. Следовательно, имеем

${\displaystyle {\begin{aligned}\ln(\exp x)&=x\\\exp(\ln y)&=y\end{aligned}}}$

для каждого действительного числа и каждого положительного действительного числа${\displaystyle x}$${\displaystyle y.}$

Экспоненциальная функция является суммой степенного ряда ^{[2] [3]} , где — факториал n (произведение n первых положительных целых чисел). Этот ряд абсолютно сходится для каждого по тесту отношения . Таким образом, производная суммы может быть вычислена путем почленного вывода, и это показывает, что сумма ряда удовлетворяет приведенному выше определению. Это второе доказательство существования и показывает, как побочный продукт, что экспоненциальная функция определена для каждого ⁠ ⁠ и является везде суммой своего ряда Маклорена .$${\displaystyle {\begin{aligned}\exp(x)&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}},\end{aligned}}}$$${\displaystyle n!}$${\displaystyle x}$${\displaystyle x}$

Экспонента удовлетворяет функциональному уравнению: Это следует из уникальности и того факта, что функция удовлетворяет приведенному выше определению. Можно доказать, что функция, удовлетворяющая этому функциональному уравнению, является экспоненциальной функцией, если ее производная в точке 0 равна 1 и функция является либо непрерывной , либо монотонной .$${\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y).}$$${\displaystyle f(x)=\exp(x+y)/\exp(y)}$

Экспоненциальная функция — это предел ^{[4] [3]} , где принимает только целые значения (в противном случае возведение в степень потребовало бы определения экспоненциальной функции). В силу непрерывности логарифма это можно доказать, взяв логарифмы и доказав, например, с помощью теоремы Тейлора .$${\displaystyle \exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n},}$$${\displaystyle n}$$${\displaystyle x=\lim _{n\to \infty }\ln \left(1+{\frac {x}{n}}\right)^{n}=\lim _{n\to \infty }n\ln \left(1+{\frac {x}{n}}\right),}$$

Положительность: Для каждого ⁠ ⁠${\displaystyle x}$ , имеем ⁠ ⁠${\displaystyle \exp(x)\neq 0}$ , поскольку функциональное уравнение подразумевает ⁠ ⁠${\displaystyle \exp(x)\exp(-x)=1}$ . Это приводит к тому, что экспоненциальная функция положительна (поскольку ⁠ ⁠${\displaystyle \exp(0)>0}$ , если бы мы имели ⁠ ⁠${\displaystyle \exp(x)<0}$ для некоторого ⁠ ⁠${\displaystyle x}$ , теорема о промежуточном значении подразумевала бы существование некоторого ⁠ ⁠${\displaystyle y}$ такого, что ⁠ ⁠${\displaystyle \exp(y)=0}$ . Это также приводит к тому, что экспоненциальная функция монотонно возрастает .

Расширение возведения в степень до положительных действительных оснований: Пусть b — положительное действительное число. Поскольку показательная функция и натуральный логарифм являются обратными друг другу, то имеем Если n — целое число, функциональное уравнение логарифма подразумевает Поскольку самое правое выражение определено, если n — любое действительное число, это позволяет определить ⁠ ⁠ для каждого положительного действительного числа b и каждого действительного числа x : В частности, если b — число Эйлера, то имеем (обратную функцию) и, таким образом, Это показывает эквивалентность двух обозначений для показательной функции.${\displaystyle b=\exp(\ln b).}$$${\displaystyle b^{n}=\exp(\ln b^{n})=\exp(n\ln b).}$$${\displaystyle b^{x}}$$${\displaystyle b^{x}=\exp(x\ln b).}$$ ${\displaystyle e=\exp(1),}$${\displaystyle \ln e=1}$$${\displaystyle e^{x}=\exp(x).}$$

Термин «экспоненциальная функция» иногда используется для обозначения любой функции, аргумент которой появляется в показателе степени , например, ⁠ ⁠${\displaystyle x\mapsto b^{x^{2}+2c}}$ и ⁠ ⁠ ${\displaystyle x\mapsto b^{c{\sqrt {x}}}.}$^[5] Однако это название обычно используется для дифференцируемых функций, удовлетворяющих одному из следующих эквивалентных условий:${\displaystyle f}$

• (i) Существуют некоторые константы ⁠ ⁠${\displaystyle a}$ и ⁠ ⁠${\displaystyle b>0}$ такие, что ⁠ ⁠${\displaystyle f(x)=ab^{x}}$ для каждого значения ⁠ ⁠${\displaystyle x}$ .
• (ii) Существуют некоторые константы ⁠ ⁠${\displaystyle a}$ и ⁠ ⁠${\displaystyle k}$ такие, что ⁠ ⁠${\displaystyle f(x)=ae^{kx},}$ для каждого значения ⁠ ⁠${\displaystyle x}$ .
• (iii) Существуют некоторые константы ⁠ ⁠${\displaystyle a}$ и ⁠ ⁠${\displaystyle \tau }$ такие, что ⁠ ⁠${\displaystyle f(x)=ae^{x/\tau },}$ для каждого значения ⁠ ⁠${\displaystyle x}$ .
• (iv) Для каждого значение не зависит от , то есть для всех u , v и d . Другими словами: пары аргументов с одинаковой разностью отображаются в пары значений с одинаковым отношением. ^{[6] [7] [8] [9]}${\displaystyle d,}$${\displaystyle f(x+d)/f(x)}$${\displaystyle x;}$$${\displaystyle {\frac {f(u+d)}{f(u)}}={\frac {f(v+d)}{f(v)}}}$$
• (v) Значение не зависит от . ^[a] Это постоянное значение иногда называют константой скорости и обозначают как ⁠ ⁠ ; оно равно константе k в (ii). ^{[b] [10] [11] [12]}   Его обратная величина, постоянное значение , в некоторых контекстах называется постоянной времени и обозначается как (so, ); оно равно константе в (iii).${\displaystyle f'(x)/f(x)}$${\displaystyle x}$${\displaystyle f}$${\displaystyle k}$${\displaystyle f(x)/f'(x)}$${\displaystyle f}$${\displaystyle \tau }$${\displaystyle \tau =1/k}$${\displaystyle \tau }$
  
• (vi) Значение не зависит от и Это постоянное значение равно константе b в (i) и называется основанием показательной функции. ^[c]$${\displaystyle \left({\frac {f(x+d)}{f(x)}}\right)^{1/d}}$$${\displaystyle x}$${\displaystyle d.}$

Основанием показательной функции является основание возведения в степень , которое появляется в ней при записи ⁠ ⁠ , а именно ⁠ ⁠ . ^[13]${\displaystyle x\to ba^{x}}$${\displaystyle b}$

Экспоненциальная функция возникает всякий раз, когда величина растет или убывает со скоростью, пропорциональной ее текущему значению. Одной из таких ситуаций является непрерывно начисляемый процент , и фактически именно это наблюдение привело Якоба Бернулли в 1683 году ^[14] к числу, теперь известному как e . Позднее, в 1697 году, Иоганн Бернулли изучал исчисление экспоненциальной функции. ^[14]$${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}$$

Если основная сумма в размере 1 приносит проценты по годовой ставке x, начисляемые ежемесячно, то проценты, получаемые каждый месяц, составляют ⁠х/12⁠ умножается на текущее значение, поэтому каждый месяц общая стоимость умножается на (1 + ⁠х/12⁠ ) ​​, а значение на конец года составляет (1 + ⁠х/12⁠ ) ^​​12. Если вместо этого проценты начисляются ежедневно, это становится (1 + ⁠х/365⁠ ) ^​​365. Если позволить числу временных интервалов в году расти без ограничений, то это приводит к предельному определению показательной функции, впервые данному Леонардом Эйлером . ^[4] Это одно из многих описаний показательной функции ; другие включают ряды или дифференциальные уравнения .$${\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$$

Из любого из этих определений можно показать, что e ^{− x} является обратной величиной e ^x . Например, из определения дифференциального уравнения e ^x e ^{− x} = 1 , когда x = 0 , а его производная с использованием правила произведения равна e ^x e ^{− x} − e ^x e ^{− x} = 0 для всех x , поэтому e ^x e ^{− x} = 1 для всех x .

Из любого из этих определений можно показать, что показательная функция подчиняется основному тождеству возведения в степень . Например, из определения степенного ряда, расширенного теоремой Бинома Ньютона , Это оправдывает показательную запись e ^x для exp x .$${\displaystyle \exp(x+y)=\sum _{n=0}^{\infty }{\frac {(x+y)^{n}}{n!}}=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {n!}{k!(n-k)!}}{\frac {x^{k}y^{n-k}}{n!}}=\sum _{k=0}^{\infty }\sum _{\ell =0}^{\infty }{\frac {x^{k}y^{\ell }}{k!\ell !}}=\exp x\cdot \exp y\,.}$$

Производная (скорость изменения) экспоненциальной функции — это сама экспоненциальная функция. В более общем смысле, функция со скоростью изменения , пропорциональной самой функции , выражается через экспоненциальную функцию. Это производное свойство приводит к экспоненциальному росту или экспоненциальному убыванию.

Экспоненциальная функция распространяется на целую функцию на комплексной плоскости . Формула Эйлера связывает ее значения при чисто мнимых аргументах с тригонометрическими функциями . Экспоненциальная функция также имеет аналоги, для которых аргумент является матрицей или даже элементом банаховой алгебры или алгебры Ли .

Важность показательной функции в математике и естественных науках обусловлена ​​главным образом ее свойством как уникальной функции, которая равна своей производной и равна 1 при x = 0. То есть,$${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.}$$

Функции вида ae ^x для постоянного a являются единственными функциями, которые равны своей производной (по теореме Пикара–Линделёфа ). Другие способы сказать то же самое включают:

• Наклон графика в любой точке равен высоте функции в этой точке.
• Скорость возрастания функции в точке x равна значению функции в точке x .
• Функция решает дифференциальное уравнение y ′ = y .
• exp — неподвижная точка производной как линейного оператора в функциональном пространстве .

Если скорость роста или убывания переменной пропорциональна ее размеру — как в случае неограниченного роста населения (см. Мальтузианская катастрофа ), непрерывного начисления сложных процентов или радиоактивного распада — то переменную можно записать как константу, умноженную на экспоненциальную функцию времени.

В более общем случае, для любой действительной константы k функция f : R → R удовлетворяет тогда и только тогда, когда для некоторой константы a . Константа k называется константой распада , константой распада , ^[15] константой скорости , ^[16] или константой превращения . ^[17]${\displaystyle f'=kf}$${\displaystyle f(x)=ae^{kx}}$

Более того, для любой дифференцируемой функции f по правилу цепочки находим :$${\displaystyle {\frac {d}{dx}}e^{f(x)}=f'(x)e^{f(x)}.}$$

Цепную дробь для e ^x можно получить с помощью тождества Эйлера :$${\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}$$

Следующая обобщенная цепная дробь для e ^z сходится быстрее: ^[18]$${\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}}$$

или, применяя замену z = ⁠х/у⁠ : с особым случаем для z = 2 :$${\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}}$$$${\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots }}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots }}}}}}}}}$$

Эта формула также сходится, хотя и медленнее, при z > 2. Например:$${\displaystyle e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots }}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots }}}}}}}}}$$

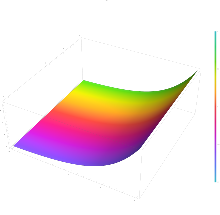
Как и в действительном случае, показательная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах.

Наиболее распространенное определение комплексной показательной функции аналогично определению степенного ряда для действительных аргументов, где действительная переменная заменяется комплексной:$${\displaystyle \exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}}$$

В качестве альтернативы комплексную экспоненциальную функцию можно определить, смоделировав определение предела для действительных аргументов, но заменив действительную переменную комплексной:$${\displaystyle \exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}}$$

Для определения степенного ряда почленное умножение двух копий этого степенного ряда в смысле Коши , допускаемое теоремой Мертенса , показывает, что определяющее мультипликативное свойство показательных функций продолжает выполняться для всех комплексных аргументов:$${\displaystyle \exp(w+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C} }$$

Определение комплексной показательной функции в свою очередь приводит к соответствующим определениям, расширяющим тригонометрические функции до комплексных аргументов.

В частности, когда z = it ( t real), определение ряда дает разложение$${\displaystyle \exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).}$$

В этом расширении перестановка членов в действительную и мнимую части оправдана абсолютной сходимостью ряда. Действительная и мнимая части приведенного выше выражения фактически соответствуют разложениям в ряды cos t и sin t соответственно.

Это соответствие дает мотивацию для определения косинуса и синуса для всех комплексных аргументов в терминах и эквивалентного степенного ряда: ^[19]${\displaystyle \exp(\pm iz)}$$${\displaystyle {\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}}$$

для всех${\textstyle z\in \mathbb {C} .}$

Функции exp , cos и sin , определенные таким образом, имеют бесконечные радиусы сходимости по тесту отношения и, следовательно, являются целыми функциями (то есть голоморфными на ). Область значений экспоненциальной функции равна , в то время как области значений комплексных функций синуса и косинуса равны обеим в полном объеме, в соответствии с теоремой Пикара , которая утверждает, что область значений непостоянной целой функции равна либо всем , либо исключая одно лакунарное значение .${\displaystyle \mathbb {C} }$${\displaystyle \mathbb {C} \setminus \{0\}}$${\displaystyle \mathbb {C} }$${\displaystyle \mathbb {C} }$${\displaystyle \mathbb {C} }$

Эти определения для показательной и тригонометрической функций тривиально приводят к формуле Эйлера :$${\displaystyle \exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .}$$

Мы могли бы альтернативно определить сложную показательную функцию, основанную на этом отношении. Если z = x + iy , где x и y оба действительны, то мы могли бы определить ее показательную функцию как где exp , cos , и sin в правой части знака определения должны интерпретироваться как функции действительной переменной, ранее определенной другими способами. ^[20]$${\displaystyle \exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)}$$

Для соотношение сохраняется, так что для вещественных и отображает вещественную линию (mod 2 π ) в единичную окружность в комплексной плоскости. Более того, переходя от к , кривая, определяемая чертит сегмент единичной окружности длиной, начинающейся от z = 1 в комплексной плоскости и идущей против часовой стрелки. Основываясь на этих наблюдениях и на том факте, что мера угла в радианах является длиной дуги на единичной окружности, стягиваемой углом, легко видеть, что, ограничиваясь вещественными аргументами, функции синуса и косинуса, определенные выше, совпадают с функциями синуса и косинуса, введенными в элементарной математике через геометрические понятия.${\displaystyle t\in \mathbb {R} }$${\displaystyle {\overline {\exp(it)}}=\exp(-it)}$${\displaystyle \left|\exp(it)\right|=1}$${\displaystyle t}$${\displaystyle t\mapsto \exp(it)}$${\displaystyle t=0}$${\displaystyle t=t_{0}}$${\displaystyle \gamma (t)=\exp(it)}$$${\displaystyle \int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},}$$

Комплексная показательная функция является периодической с периодом 2 πi и справедлива для всех .${\displaystyle \exp(z+2\pi ik)=\exp z}$${\displaystyle z\in \mathbb {C} ,k\in \mathbb {Z} }$

При расширении области определения от действительной прямой до комплексной плоскости экспоненциальная функция сохраняет следующие свойства:$${\displaystyle {\begin{aligned}&e^{z+w}=e^{z}e^{w}\\[5pt]&e^{0}=1\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}}$$

для всех${\textstyle w,z\in \mathbb {C} .}$

Расширение натурального логарифма до комплексных аргументов дает комплексный логарифм log z , который является многозначной функцией .

Затем мы можем определить более общее возведение в степень: для всех комплексных чисел z и w . Это также многозначная функция, даже когда z является действительным числом. Это различие проблематично, поскольку многозначные функции log z и z ^w легко спутать с их однозначными эквивалентами при замене z действительным числом . Правило умножения показателей степеней для случая положительных действительных чисел должно быть изменено в многозначном контексте:$${\displaystyle z^{w}=e^{w\log z}}$$

Более подробную информацию о проблемах с объединением степеней см . в разделе «Несостоятельность тождеств степеней и логарифмов» .

Экспоненциальная функция отображает любую линию в комплексной плоскости в логарифмическую спираль в комплексной плоскости с центром в начале координат . Существуют два особых случая: когда исходная линия параллельна действительной оси, результирующая спираль никогда не замыкается сама на себя; когда исходная линия параллельна мнимой оси, результирующая спираль представляет собой окружность некоторого радиуса.

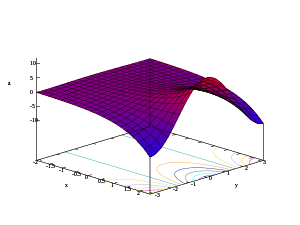
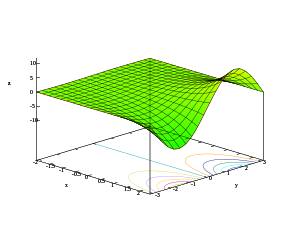
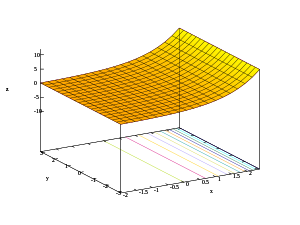
• 3D-графики действительной части, мнимой части и модуля показательной функции
• 
  z ⁼ Re( екс ^{+ iy} )
• 
  z = Im( е ^{x + iy} )
• 
  z = ^| ex ^{+ iy} |

Рассматривая сложную показательную функцию как функцию, включающую четыре действительные переменные: график показательной функции представляет собой двумерную поверхность, искривленную в четырех измерениях.$${\displaystyle v+iw=\exp(x+iy)}$$

Начиная с цветной части домена , ниже приведены изображения графика, проецируемого по-разному в двух- или трехмерном пространстве.${\displaystyle xy}$

• Графики комплексной показательной функции
• 
  Ключ к шахматной доске:
  ${\displaystyle x>0:\;{\text{green}}}$
  ${\displaystyle x<0:\;{\text{red}}}$
  ${\displaystyle y>0:\;{\text{yellow}}}$
  ${\displaystyle y<0:\;{\text{blue}}}$
• 
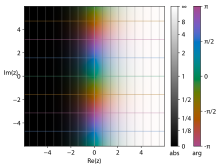
  Проекция на комплексную плоскость дальности (V/W). Сравните со следующим, перспективным изображением.
• 
  Проекция в измерения , , и , создающая форму расширяющегося рога или воронки (представленную как двухмерное перспективное изображение)${\displaystyle x}$${\displaystyle v}$${\displaystyle w}$
• 
  Проекция в измерения , , и , создающая спиральную форму ( диапазон расширен до ±2 π , снова как двухмерное перспективное изображение)${\displaystyle y}$${\displaystyle v}$${\displaystyle w}$${\displaystyle y}$

На втором рисунке показано, как комплексная плоскость домена отображается в комплексную плоскость диапазона:

• ноль отображается как 1
• действительная ось отображается на положительную действительную ось${\displaystyle x}$${\displaystyle v}$
• мнимая ось вращается вокруг единичной окружности с постоянной угловой скоростью${\displaystyle y}$
• значения с отрицательными действительными частями отображаются внутри единичной окружности
• значения с положительными действительными частями отображаются за пределами единичной окружности
• значения с постоянной действительной частью отображаются в виде окружностей с центром в нуле
• значения с постоянной мнимой частью отображаются в лучи, исходящие из нуля

Третье и четвертое изображения показывают, как график на втором изображении расширяется в одно из двух других измерений, не показанных на втором изображении.

Третье изображение показывает график, вытянутый вдоль действительной оси. Оно показывает, что график является поверхностью вращения вокруг оси графика действительной экспоненциальной функции, образуя форму рога или воронки.${\displaystyle x}$${\displaystyle x}$

Четвертое изображение показывает график, расширенный вдоль мнимой оси. Оно показывает, что поверхность графика для положительных и отрицательных значений на самом деле не встречается вдоль отрицательной действительной оси, а вместо этого образует спиральную поверхность вокруг оси. Поскольку его значения были расширены до ±2 π , это изображение также лучше отображает периодичность 2π в мнимом значении.${\displaystyle y}$${\displaystyle y}$${\displaystyle v}$${\displaystyle y}$${\displaystyle y}$${\displaystyle y}$

Определение степенного ряда показательной функции имеет смысл для квадратных матриц (для которых функция называется матричной показательной функцией ) и, в более общем случае, в любой унитальной банаховой алгебре B. В этом случае e ⁰ = 1 , и e ^x обратим с обратным e ^{− x} для любого x из B. Если xy = yx , то e ^{x + y} = e ^x e ^y , но это тождество может не выполняться для некоммутирующих x и y .

Некоторые альтернативные определения приводят к той же функции. Например, e ^x можно определить как$${\displaystyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$$

Или e ^x можно определить как f _x (1) , где f _x  : R → B — решение дифференциального уравнения ⁠дф _х/дт⁠ ( t ) = x  f _x ( t ) , с начальным условием f _x (0) = 1 ; отсюда следует, что f _x ( t ) = e ^tx для любого t в R .

Если задана группа Ли G и ее связанная алгебра Ли , то экспоненциальное отображение является отображением ↦ G , удовлетворяющим аналогичным свойствам. Фактически, поскольку R является алгеброй Ли группы Ли всех положительных действительных чисел при умножении, то обычная экспоненциальная функция для действительных аргументов является частным случаем ситуации алгебры Ли. Аналогично, поскольку группа Ли GL( n , R ) обратимых матриц размера n × n имеет в качестве алгебры Ли M( n , R ) , пространства всех матриц размера n × n , то экспоненциальная функция для квадратных матриц является частным случаем экспоненциального отображения алгебры Ли.${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {g}}}$

Тождество может не выполняться для элементов алгебры Ли x и y , которые не коммутируют; формула Бейкера–Кэмпбелла–Хаусдорфа обеспечивает необходимые поправочные члены.${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

Функция e ^z не принадлежит кольцу рациональных функций : она не является частным двух многочленов с комплексными коэффициентами.${\displaystyle \mathbb {C} (z)}$

Если a ₁ , ..., a _n — различные комплексные числа, то e a ^{1 _z ,} ..., e ^{a _n z} линейно независимы над , и, следовательно, e ^z трансцендентно над .${\displaystyle \mathbb {C} (z)}$${\displaystyle \mathbb {C} (z)}$

Определение ряда Тейлора выше, как правило, эффективно для вычисления (приближения) . Однако при вычислении вблизи аргумента результат будет близок к 1, а вычисление значения разности с помощью арифметики с плавающей точкой может привести к потере (возможно, всех) значащих цифр , что приведет к большой относительной ошибке, возможно, даже к бессмысленному результату.${\displaystyle e^{x}}$${\displaystyle x=0}$${\displaystyle e^{x}-1}$

Следуя предложению Уильяма Кахана , может быть полезно иметь специальную процедуру, часто называемую expm1, которая вычисляет e ^x − 1 напрямую, минуя вычисление e ^x . Например, можно использовать ряд Тейлора:$${\displaystyle e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots .}$$

Впервые это было реализовано в 1979 году в калькуляторе Hewlett-Packard HP-41C и поддерживалось несколькими калькуляторами, ^{[21] [22]} операционными системами (например, Berkeley UNIX 4.3BSD ^[23] ), системами компьютерной алгебры и языками программирования (например, C99 ). ^[24]

Помимо основания e , стандарт IEEE 754-2008 определяет аналогичные экспоненциальные функции вблизи 0 для оснований 2 и 10: и .${\displaystyle 2^{x}-1}$${\displaystyle 10^{x}-1}$

Аналогичный подход использовался для логарифма; см. log1p .

Тождество в терминах гиперболического тангенса дает высокоточное значение для малых значений x в системах, которые не реализуют expm1( x ) .$${\displaystyle \operatorname {expm1} (x)=e^{x}-1={\frac {2\tanh(x/2)}{1-\tanh(x/2)}},}$$

• «Экспоненциальная функция», Энциклопедия математики , EMS Press , 2001 [1994]