Азартные игры и теория информации

Статистический вывод можно рассматривать как теорию азартных игр, применяемую к окружающему нас миру. Множество приложений для логарифмических информационных мер точно говорят нам, как сделать наилучшее предположение в условиях частичной информации. ^[1] В этом смысле теорию информации можно считать формальным выражением теории азартных игр. Поэтому неудивительно, что теория информации имеет приложения к азартным играм. ^[2]

Ставки Келли или пропорциональные ставки — это применение теории информации к инвестированию и азартным играм . Ее первооткрывателем был Джон Ларри Келли-младший .

Часть идеи Келли заключалась в том, чтобы игрок максимизировал ожидание логарифма своего капитала, а не ожидаемую прибыль от каждой ставки. Это важно, поскольку в последнем случае игрок был бы вынужден поставить все, что у него было, когда ему представилась бы выгодная ставка, и если бы он проиграл, у него не было бы капитала, с которым он мог бы делать последующие ставки. Келли понял, что именно логарифм капитала игрока является аддитивным в последовательных ставках, и «к которому применим закон больших чисел».

Бит — это количество энтропии в событии, на которое можно делать ставки, с двумя возможными исходами и равными шансами. Очевидно, мы могли бы удвоить наши деньги, если бы заранее знали, каким будет исход этого события. Идея Келли заключалась в том, что независимо от того, насколько сложен сценарий ставок, мы можем использовать оптимальную стратегию ставок, называемую критерием Келли , чтобы заставить наши деньги расти экспоненциально с любой побочной информацией, которую мы можем получить. Ценность этой «незаконной» побочной информации измеряется как взаимная информация относительно результата события, на которое можно делать ставки:

${\displaystyle {\begin{align}I(X;Y)&=\mathbb {E} _{Y}\{D_{\mathrm {KL} }{\big (}P(X|Y)\|P(X|I){\big )}\}\\&=\mathbb {E} _{Y}\{D_{\mathrm {KL} }{\big (}P(X|{\textrm {сторона}}\ {\textrm {информация}}\ Y)\|P(X|{\textrm {заявлено}}\ {\textrm {шансы}}\ I){\big )}\},\end{align}}}$

где Y — побочная информация, X — результат события, на которое можно сделать ставку, а I — состояние знаний букмекера. Это среднее расхождение Кульбака–Лейблера , или прирост информации, апостериорного распределения вероятностей X, заданного значением Y относительно априорного распределения или заявленных коэффициентов на X. Обратите внимание, что ожидание берется по Y, а не по X : нам нужно оценить, насколько точна в долгосрочной перспективе наша побочная информация Y , прежде чем мы начнем делать ставки на реальные деньги на X. Это прямое применение байесовского вывода . Обратите внимание, что побочная информация Y может повлиять не только на наши знания о событии X, но и на само событие. Например, Y может быть лошадью, у которой было слишком много овса или недостаточно воды. В этом случае применяется та же математика, потому что с точки зрения букмекера случайные договорные скачки уже учтены, когда он делает свои коэффициенты.

Природа побочной информации чрезвычайно капризна. Мы уже видели, что она может влиять на фактическое событие, а также на наше знание результата. Предположим, у нас есть информатор, который сообщает нам, что победит определенная лошадь. Мы, конечно, не хотим ставить все наши деньги на эту лошадь только на слух: этот информатор может делать ставки на другую лошадь и может распространять слухи только для того, чтобы самому получить лучшие коэффициенты. Вместо этого, как мы уже указывали, нам нужно оценить нашу побочную информацию в долгосрочной перспективе, чтобы увидеть, как она коррелирует с результатами скачек. Таким образом, мы можем точно определить, насколько надежен наш информатор, и делать ставки именно так, чтобы максимизировать ожидаемый логарифм нашего капитала в соответствии с критерием Келли. Даже если наш информатор лжет нам, мы все равно можем получить прибыль от его лжи, если сможем найти некоторую обратную корреляцию между его советами и фактическими результатами скачек.

Удвоение ставок на скачках составляет [ ^3]

${\displaystyle W(b,p)=\mathbb {E} [\log _{2}S(X)]=\sum _{i=1}^{m}p_{i}\log _{2}b_{i}o_{i}}$

где есть лошади, вероятность выигрыша th лошади равна , доля ставки на лошадь равна , а шансы (выплата) равны (например, если выигрыш th лошади приносит двойную сумму ставки). Это количество максимизируется пропорциональной (Келли) азартной игрой:${\displaystyle м}$${\displaystyle я}$${\displaystyle p_{i}}$${\displaystyle b_{i}}$${\displaystyle o_{i}}$${\displaystyle o_{i}=2}$${\displaystyle я}$

${\displaystyle b=p\,}$

для которого

${\displaystyle \max _{b}W(b,p)=\sum _{i}p_{i}\log _{2}o_{i}-H(p)\,}$

где информационная энтропия .${\displaystyle H(p)}$

Существует важная, но простая связь между объемом побочной информации, которую получает игрок, и ожидаемым экспоненциальным ростом его капитала (Келли):

${\displaystyle \mathbb {E} \log K_{t}=\log K_{0}+\sum _{i=1}^{t}H_{i}}$

для оптимальной стратегии ставок, где — начальный капитал, — капитал после t -й ставки, — объем побочной информации, полученной относительно i -й ставки (в частности, взаимная информация относительно исхода каждого события, на которое можно сделать ставку).${\displaystyle К_{0}}$${\displaystyle K_{t}}$${\displaystyle H_{i}}$

Это уравнение применимо при отсутствии каких-либо транзакционных издержек или минимальных ставок. Когда применяются эти ограничения (как это неизменно происходит в реальной жизни), в игру вступает еще одна важная концепция азартных игр: в игре с отрицательным ожидаемым значением игрок (или недобросовестный инвестор) должен столкнуться с определенной вероятностью окончательного краха, что известно как сценарий краха игрока . Обратите внимание, что даже еда, одежда и жилье могут считаться фиксированными транзакционными издержками и, таким образом, способствовать вероятности окончательного краха игрока.

Это уравнение было первым применением теории информации Шеннона за пределами ее преобладающей парадигмы передачи данных (Пирс).

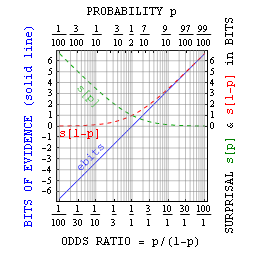
Логарифмическая мера вероятности самоинформации или неожиданности, ^[4] чье среднее значение есть информационная энтропия /неопределенность, а чья средняя разность есть KL-дивергенция , сама по себе имеет приложения к анализу шансов. Ее две основные сильные стороны в том, что неожиданности: (i) уменьшают крохотные вероятности до чисел управляемого размера, и (ii) добавляются всякий раз, когда вероятности умножаются.

Например, можно сказать, что "количество состояний равно двум к количеству битов", т.е. #состояния = 2 ^#биты . Здесь величина, измеряемая в битах, является логарифмической мерой информации, упомянутой выше. Следовательно, есть N бит неожиданности в выпадении всех орлов при первом подбрасывании N монет.

Аддитивная природа неожиданностей и способность человека почувствовать их значение с помощью горсти монет могут помочь человеку поместить невероятные события (например, выигрыш в лотерею или несчастный случай) в контекст. Например, если один из 17 миллионов билетов оказывается выигрышным, то неожиданность выигрыша от одного случайного выбора составляет около 24 бит. Подбрасывание 24 монет несколько раз может дать вам возможность почувствовать неожиданность выпадения всех орлов с первой попытки.

Аддитивная природа этой меры также оказывается полезной при взвешивании альтернатив. Например, представьте, что неожиданность вреда от вакцинации составляет 20 бит. Если неожиданность заражения болезнью без нее составляет 16 бит, но неожиданность вреда от болезни, если вы ею заразитесь, составляет 2 бита, то неожиданность вреда от НЕполучения вакцины составляет всего 16+2=18 бит. Независимо от того, решите ли вы сделать прививку или нет (например, денежная стоимость ее оплаты не включена в это обсуждение), вы можете таким образом, по крайней мере, взять на себя ответственность за решение, информированное о том факте, что неполучение вакцины влечет за собой более одного бита дополнительного риска.

В более общем смысле можно связать вероятность p с битами сюрпризов sbits как вероятность = 1/2 ^sbits . Как предполагалось выше, это в основном полезно с малыми вероятностями. Однако Джейнс указал, что с истинно-ложными утверждениями можно также определить биты доказательств ebits как сюрприз против минус сюрприз для. Это свидетельство в битах просто относится к отношению шансов = p/(1-p) = 2 ^ebits и имеет преимущества, аналогичные преимуществам самой самоинформации.

Теорию информации можно рассматривать как способ количественной оценки информации, чтобы принять наилучшее решение в условиях несовершенной информации. То есть, как принять наилучшее решение, используя только имеющуюся у вас информацию. Смысл ставок заключается в рациональной оценке всех соответствующих переменных неопределенной игры/гонки/матча, а затем в сравнении их с оценками букмекера, которые обычно имеют форму коэффициентов или спредов, и в размещении правильной ставки, если оценки существенно различаются. ^[5] Область азартных игр, где это наиболее применимо, — это ставки на спорт. Спортивный гандикап очень хорошо поддается теории информации из-за доступности статистики. В течение многих лет известные экономисты проверяли различные математические теории, используя спорт в качестве своей лаборатории, с существенно различающимися результатами.

Одна из теорий относительно ставок на спорт заключается в том, что это случайное блуждание . Случайное блуждание — это сценарий, в котором новая информация, цены и доходность будут колебаться случайно, это часть гипотезы эффективного рынка . Основополагающее убеждение гипотезы эффективного рынка заключается в том, что рынок всегда будет вносить коррективы в соответствии с любой новой информацией. Поэтому никто не может победить рынок, потому что они торгуют на той же информации, на основе которой рынок скорректировался. Однако, по словам Фамы, ^[6] для того, чтобы иметь эффективный рынок, необходимо соблюдение трех качеств:

• При торговле ценными бумагами транзакционные издержки отсутствуют
• Вся имеющаяся информация доступна всем участникам рынка бесплатно.
• Все согласны с последствиями текущей информации для текущей цены и распределения будущих цен каждой ценной бумаги.

Статистики показали, что это третье условие, которое позволяет теории информации быть полезной в спортивном гандикапе. Когда все не согласны с тем, как информация повлияет на исход события, мы получаем разные мнения.

• Принцип безразличия
• Статистическая ассоциация футбольных прогнозов
• Расширенная статистика НФЛ

• Статистический анализ в моделях спортивного гандикапа
• DVOA как объясняющая переменная