Групповой метод обработки данных

Групповой метод обработки данных ( ГМОД ) — это семейство индуктивных алгоритмов для компьютерного математического моделирования многопараметрических наборов данных, включающее полностью автоматическую структурную и параметрическую оптимизацию моделей.

GMDH используется в таких областях, как интеллектуальный анализ данных , обнаружение знаний , прогнозирование , моделирование сложных систем , оптимизация и распознавание образов . ^[1] Алгоритмы GMDH характеризуются индуктивной процедурой, которая выполняет сортировку постепенно усложняющихся полиномиальных моделей и выбор наилучшего решения с помощью внешнего критерия . Последний раздел ^[2] содержит сводку приложений GMDH в 1970-х годах.

Другие названия включают «полиномиальную нейронную сеть прямого распространения» ^[3] или «самоорганизация моделей». Это был один из первых методов глубокого обучения , использованный для обучения восьмислойной нейронной сети в 1971 году. ^{[4] [5]}

Этот раздел основан на. ^[2]

Это общая проблема статистического моделирования данных: Рассмотрим набор данных с точками. Каждая точка содержит наблюдения и одну цель для прогнозирования. Как лучше всего предсказать цель на основе наблюдений?${\displaystyle \{(x_{1},...,x_{k};y)_{s}\}_{s=1:n}}$${\displaystyle n}$${\displaystyle x_{1},...,x_{k}}$${\displaystyle у}$

Сначала мы разделили весь набор данных на две части: обучающий набор и проверочный набор. Обучающий набор будет использоваться для подгонки все большего количества параметров модели, а проверочный набор будет использоваться для принятия решения о том, какие параметры следует включить, а когда следует полностью прекратить подгонку.

GMDH начинается с рассмотрения полинома степени 2 от 2 переменных. Предположим, мы хотим предсказать цель , используя только части наблюдения и используя только полиномы степени 2, тогда самое большее, что мы можем сделать, это: где параметры вычисляются с помощью линейной регрессии . Теперь параметры зависят от того, что мы выбрали, и мы не знаем, что нам следует выбрать, поэтому мы выбираем их все. То есть, мы выполняем все такие полиномиальные регрессии: получаем полиномиальные модели набора данных.${\displaystyle я,j}$$${\displaystyle y\approx f_{a,b,c,d,e,h}(x_{i},x_{j}):=a+bx_{i}+cx_{j}+dx_{i}^{2}+ex_{j}^{2}+fx_{i}x_{j}}$$${\displaystyle а,б,в,г,д,е}$${\displaystyle а,б,в,г,д,е}$${\displaystyle я,j}$${\displaystyle я,j}$${\displaystyle {\frac {1}{2}}k(k-1)}$$${\displaystyle y\approx f_{(i,j);a,b,c,d,e,h}(x_{i},x_{j}):=a_{i,j}+b_{i,j}x_{i}+c_{i,j}x_{j}+d_{i,j}x_{i}^{2}+e_{i,j}x_{j}^{2}+f_{i,j}x_{i}x_{j}\quad \forall 1\leq i<j\leq k}$$${\displaystyle {\frac {1}{2}}k(k-1)}$

Мы не хотим принимать все полиномиальные модели, поскольку это будет содержать слишком много моделей. Чтобы выбрать только лучшее подмножество этих моделей, мы запускаем каждую модель на наборе данных проверки и выбираем модели, среднеквадратическая ошибка которых ниже порогового значения. Мы также записываем наименьшую достигнутую среднеквадратичную ошибку как .${\displaystyle f_{(i,j);a,b,c,d,e,h}}$${\displaystyle minMSE_{1}}$

Предположим, что после этого процесса мы получили набор моделей. Теперь мы запускаем модели на обучающем наборе данных, чтобы получить последовательность преобразованных наблюдений: . Тот же алгоритм теперь можно запустить снова.${\displaystyle k_{1}}$${\displaystyle z_{1},z_{2},...,z_{k_{1}}}$

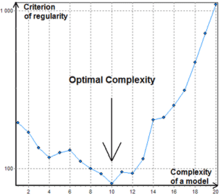
Алгоритм продолжается, давая нам . Пока каждый меньше предыдущего, процесс продолжается, давая нам все более глубокие модели. Как только некоторые , алгоритм завершается. Последний подобранный слой (слой ) отбрасывается, так как он переобучил обучающий набор. Предыдущие слои выводятся.${\displaystyle minMSE_{1},minMSE_{2},...}$${\displaystyle minMSE}$${\displaystyle minMSE_{L+1}>minMSE_{L}}$${\displaystyle L+1}$

Возможны более сложные методы принятия решения о том, когда следует прекратить работу. Например, можно продолжить выполнение алгоритма еще на несколько шагов в надежде на прохождение временного повышения .${\displaystyle minMSE}$

Вместо полинома второй степени от двух переменных каждый блок может использовать полиномы более высокой степени от большего количества переменных: ^[1]

${\displaystyle Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{n}{a_{i}}x_{i}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{a_{ij}}}x_{i}x_{j}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{\sum \limits _{k=j}^{n}{a_{ijk}}}}x_{i}x_{j}x_{k}+\cdots }$

И в более общем смысле, модель МГУА с несколькими входами и одним выходом представляет собой подмножество компонентов базовой функции (1):

${\displaystyle Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{m}a_{i}f_{i}}$

где f _i — элементарные функции, зависящие от различных наборов входных данных, a _i — коэффициенты, а m — число компонентов базовой функции.

Внешние критерии — это цели оптимизации для модели, такие как минимизация среднеквадратической ошибки на проверочном наборе, как указано выше. Наиболее распространенными критериями являются:

• Критерий регулярности (CR) – наименьшие средние квадраты на проверочном наборе.
• Наименьшие квадраты на наборе перекрестной проверки .
• Критерий минимального смещения или согласованности – квадрат разности между предполагаемыми выходными данными (или векторами коэффициентов) двух моделей, соответствующих наборам A и B, деленный на квадраты прогнозов на наборе B. ^[1]

Подобно линейной регрессии, которая подбирает линейное уравнение по данным, МГУА подбирает произвольно высокие порядки полиномиальных уравнений по данным. ^{[6] [7]}

Для выбора между моделями используются два или более подмножества выборки данных, аналогично разделению на обучение-проверку-тест .

GMDH объединила идеи из: ^[8] моделирования черного ящика , последовательного генетического отбора парных признаков , ^[9] принципа Габора « свободы выбора решений», ^[10] и принципа Бира внешних дополнений. ^[11]

Вдохновленные аналогией между построением модели из зашумленных данных и отправкой сообщений по зашумленному каналу , ^[12] они предложили «помехоустойчивое моделирование»: ^[6] чем выше уровень шума, тем меньше параметров должна иметь оптимальная модель, поскольку зашумленный канал не позволяет передавать больше битов.

Модель структурирована как нейронная сеть прямого распространения, но без ограничений по глубине, в ней реализована процедура автоматической генерации структуры моделей, имитирующая процесс биологического отбора по парным генетическим признакам.

Метод был создан в 1968 году профессором Алексеем Григорьевичем Ивахненко в Институте кибернетики в Киеве .

Период 1968–1971 гг. характеризуется применением только критерия регулярности для решения задач идентификации, распознавания образов и краткосрочного прогнозирования. В качестве опорных функций использовались полиномы, логические сети, нечеткие множества Заде и формулы вероятностей Байеса. Авторов стимулировала очень высокая точность прогнозирования при новом подходе. Помехоустойчивость не исследовалась.

Период 1972–1975 гг . Решена проблема моделирования зашумленных данных и неполной информационной базы. Предложены многокритериальный отбор и использование дополнительной априорной информации для повышения помехоустойчивости. Лучшие эксперименты показали, что при расширенном определении оптимальной модели по дополнительному критерию уровень шума может быть в десять раз больше сигнала. Затем он был улучшен с использованием теоремы Шеннона общей теории связи.

Период 1976–1979 гг . Исследована сходимость многослойных алгоритмов МГУА. Показано, что некоторые многослойные алгоритмы имеют «ошибку многослойности» – аналогичную статической ошибке систем управления. В 1977 г. предложено решение задач анализа целевых систем многослойными алгоритмами МГУА. Оказалось, что перебор по ансамблю критериев позволяет найти единственно оптимальную систему уравнений и, следовательно, показать элементы сложного объекта, их основные входные и выходные переменные.

Период 1980–1988 гг . Получено много важных теоретических результатов. Стало ясно, что полные физические модели не могут быть использованы для долгосрочного прогнозирования. Доказано, что нефизические модели МГУА более точны для аппроксимации и прогноза, чем физические модели регрессионного анализа. Разработаны двухуровневые алгоритмы, использующие для моделирования два различных масштаба времени.

Начиная с 1989 года разрабатывались и исследовались новые алгоритмы (AC, OCC, PF) для непараметрического моделирования нечетких объектов и SLP для экспертных систем. ^[13] Современный этап развития GMDH можно охарактеризовать как расцвет нейросетей глубокого обучения и параллельных индуктивных алгоритмов для многопроцессорных компьютеров. Такая процедура в настоящее время используется в сетях глубокого обучения . ^[14]

Существует множество различных способов выбора порядка рассмотрения частичных моделей. Самый первый порядок рассмотрения, используемый в GMDH и первоначально называемый многослойной индуктивной процедурой, является самым популярным. Он представляет собой сортировку постепенно усложняющихся моделей, сгенерированных из базовой функции . Лучшая модель указывается минимумом характеристики внешнего критерия. Многослойная процедура эквивалентна искусственной нейронной сети с полиномиальной функцией активации нейронов. Поэтому алгоритм с таким подходом обычно называют нейронной сетью типа GMDH или полиномиальной нейронной сетью. Ли показал, что нейронная сеть типа GMDH работает лучше, чем классические алгоритмы прогнозирования, такие как Single Exponential Smooth, Double Exponential Smooth, ARIMA и нейронная сеть обратного распространения. ^[15]

Другим важным подходом к рассмотрению частичных моделей, который становится все более популярным, является комбинаторный поиск, который является либо ограниченным, либо полным. Этот подход имеет некоторые преимущества по сравнению с полиномиальными нейронными сетями, но требует значительной вычислительной мощности и, таким образом, неэффективен для объектов с большим количеством входов. Важным достижением комбинаторного МГУА является то, что он полностью превосходит подход линейной регрессии, если уровень шума во входных данных больше нуля. Он гарантирует, что наиболее оптимальная модель будет найдена в ходе исчерпывающей сортировки.

Базовый комбинаторный алгоритм выполняет следующие шаги:

• Делит выборку данных как минимум на две выборки A и B.
• Генерирует подвыборки из A в соответствии с частичными моделями с постоянно возрастающей сложностью.
• Оценивает коэффициенты частичных моделей на каждом уровне сложности моделей.
• Рассчитывает значение внешнего критерия для моделей на выборке B.
• Выбирает лучшую модель (набор моделей), указанную по минимальному значению критерия.
• Для выбранной модели оптимальной сложности пересчитать коэффициенты на всей выборке данных.

В отличие от нейронных сетей типа МГУА комбинаторный алгоритм обычно не останавливается на определенном уровне сложности, поскольку точка увеличения значения критерия может быть просто локальным минимумом, см. рис.1.

• Комбинаторный (КОМБИ)
• Многослойный итеративный (MIA)
• ГН
• Объективный системный анализ (OSA)
• Гармонический
• Двухуровневый (АРИМАД)
• Мультипликативно-аддитивный (МАА)
• Объективная компьютерная кластеризация (OCC);
• Алгоритм кластеризации «Указывая пальцем» (PF);
• Аналоги Комплексообразующие (АК)
• Гармоническая передискретизация
• Алгоритм на основе Многослойной Теории Статистических Решений (МТСР)
• Группа адаптивных моделей эволюции (GAME)

• Проект FAKE GAME — Открытый исходный код. Кроссплатформенный.
• GEvom — Бесплатно по запросу для академического использования. Только для Windows.
• GMDH Shell — программное обеспечение для прогнозной аналитики и прогнозирования временных рядов на основе GMDH. Доступны бесплатная академическая лицензия и бесплатная пробная версия. Только для Windows.
• KnowledgeMiner — Коммерческий продукт. Только для Mac OS X. Доступна бесплатная демоверсия.
• Клиент PNN Discovery — коммерческий продукт.
• Sciengy RPF! — Бесплатное ПО с открытым исходным кодом.
• wGMDH — плагин Weka , с открытым исходным кодом.
• Пакет R – Открытый исходный код.
• Пакет R для задач регрессии – Открытый исходный код.
• Библиотека Python алгоритма MIA — с открытым исходным кодом.
• Библиотека Python базовых алгоритмов МГУА (COMBI, MULTI, MIA, RIA) - с открытым исходным кодом.

• Ивахненко А. Г. Эвристическая самоорганизация в задачах технической кибернетики, Автоматика, т. 6, 1970 — С. 207-219.
• SJ Farlow . Самоорганизующиеся методы в моделировании: алгоритмы типа GMDH . Нью-Йорк, Базель: Marcel Decker Inc., 1984, 350 стр.
• HR Madala, AG Ivakhnenko. Алгоритмы индуктивного обучения для моделирования сложных систем. CRC Press, Boca Raton, 1994.

• Библиотека книг и статей МГУА
• Групповой метод обработки данных