Закон Фиттса

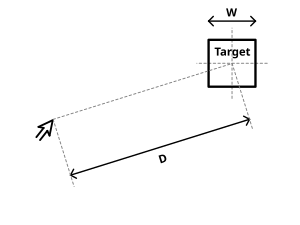
Закон Фиттса (часто упоминаемый как закон Фиттса ) — это предиктивная модель движения человека, в основном используемая во взаимодействии человека с компьютером и эргономике . Закон предсказывает, что время, необходимое для быстрого перемещения в целевую область, является функцией соотношения между расстоянием до цели и шириной цели. ^[1] Закон Фиттса используется для моделирования акта указания , либо путем физического прикосновения к объекту рукой или пальцем, либо виртуально, путем указания на объект на мониторе компьютера с помощью указательного устройства . Первоначально он был разработан Полом Фиттсом .

Закон Фиттса, как было показано, применим в различных условиях: с различными конечностями (руки, ноги, ^[2] нижняя губа, ^[3] прицелы, закрепленные на голове ^[4] ), манипуляторами (устройствами ввода), ^[5] физическими средами (включая подводные ^[6] ) и группами пользователей (молодые, пожилые ^[7] лица с особыми образовательными потребностями ^[8] и участники, находящиеся под воздействием наркотиков ^[9] ).

В оригинальной статье 1954 года Пола Морриса Фиттса была предложена метрика для количественной оценки сложности задачи выбора цели. Метрика была основана на информационной аналогии, где расстояние до центра цели ( D ) подобно сигналу, а допуск или ширина цели ( W ) подобны шуму. Метрика представляет собой индекс сложности Фиттса ( ID , в битах):

$${\displaystyle {\text{ID}}=\log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}}$$

Фиттс также предложил индекс производительности ( IP , в битах в секунду) в качестве меры производительности человека. Метрика объединяет индекс сложности задачи ( ID ) со временем движения ( MT , в секундах) при выборе цели. По словам Фиттса, «средняя скорость информации, генерируемой серией движений, — это средняя информация за движение, деленная на время за движение». ^[1] Таким образом,

$${\displaystyle {\text{IP}}={\Bigg (}{\frac {\text{ID}}{\text{MT}}}{\Bigg )}}$$

Сегодня IP чаще называют пропускной способностью ( TP ). Также принято включать поправку на точность в расчет.

Исследователи после Фиттса начали практиковать построение уравнений линейной регрессии и проверку корреляции ( r ) на предмет соответствия. Уравнение выражает связь между MT и параметрами задач D и W :

$${\displaystyle {\text{MT}}=a+b\cdot {\text{ID}}=a+b\cdot \log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}}$$

где:

• МТ — среднее время завершения движения.
• a и b — константы, зависящие от выбора входного устройства и обычно определяемые эмпирически с помощью регрессионного анализа . a определяет пересечение на оси y и часто интерпретируется как задержка. Параметр b — это наклон, описывающий ускорение. Оба параметра показывают линейную зависимость в законе Фиттса. ^[10]
• ID — индекс сложности.
• D — расстояние от начальной точки до центра мишени.
• W — ширина цели, измеренная вдоль оси движения. W также можно рассматривать как допустимую погрешность в конечном положении, поскольку конечная точка движения должна находиться в пределах ± W ⁄ 2 от центра цели.

Поскольку для данной задачи желательно более короткое время перемещения, значение параметра b можно использовать в качестве метрики при сравнении компьютерных указательных устройств друг с другом. Первое применение закона Фиттса в человеко-машинном интерфейсе было сделано Кардом, Инглишем и Берром ^[11], которые использовали индекс производительности ( IP ), интерпретируемый как 1 ⁄ b , для сравнения производительности различных устройств ввода , при этом мышь оказалась выше по сравнению с джойстиком или клавишами направленного перемещения. ^[11] Эта ранняя работа, согласно биографии Стюарта Карда , «была основным фактором, приведшим к коммерческому внедрению мыши компанией Xerox ». ^[12]

Многие эксперименты, проверяющие закон Фиттса, применяют модель к набору данных, в котором варьируются либо расстояние, либо ширина, но не оба. Предсказательная сила модели ухудшается, когда оба варьируются в значительном диапазоне. ^[13] Обратите внимание, что поскольку термин ID зависит только от отношения расстояния к ширине, модель подразумевает, что целевое расстояние и комбинация ширины могут быть произвольно изменены без влияния на время движения, что невозможно. Несмотря на свои недостатки, эта форма модели обладает замечательной предсказательной силой в диапазоне модальностей компьютерного интерфейса и двигательных задач и предоставила множество идей о принципах проектирования пользовательского интерфейса.

Движение во время выполнения одной задачи по закону Фиттса можно разделить на две фазы: ^[10]

• Начальное движение . Быстрое, но неточное движение к цели.
• Финальное движение . Более медленное, но более точное движение для того, чтобы захватить цель.

Первая фаза определяется расстоянием до цели. В этой фазе расстояние может быть сокращено быстро, оставаясь при этом неточным. Второе движение пытается выполнить медленное и контролируемое точное движение, чтобы фактически поразить цель. Длительность задачи линейно масштабируется в зависимости от сложности. ^[10] Но поскольку разные задачи могут иметь одинаковую сложность, выводится, что расстояние оказывает большее влияние на общее время выполнения задачи, чем размер цели.

Часто цитируется, что закон Фиттса может быть применен к отслеживанию глаз . Это кажется по крайней мере спорной темой, как показал Дрюс. ^[14] Во время быстрых саккадических движений глаз пользователь слеп. Во время выполнения задачи по закону Фиттса пользователь сознательно захватывает свою цель и может фактически видеть ее, что делает эти два типа взаимодействия несопоставимыми.

Формулировка индекса сложности Фиттса, наиболее часто используемая в сообществе специалистов по взаимодействию человека с компьютером, называется формулой Шеннона:

$${\displaystyle {\text{ID}}=\log _{2}{\Bigg (}{\frac {D}{W}}+1{\Bigg )}}$$

Эта форма была предложена Скоттом Маккензи, ^[15] профессором Йоркского университета , и названа так из-за ее сходства с теоремой Шеннона–Хартли . ^[16] Она описывает передачу информации с использованием полосы пропускания, силы сигнала и шума. В законе Фиттса расстояние представляет силу сигнала, а ширина цели — шум.

Используя эту форму модели, сложность задачи указания была приравнена к количеству информации, переданной (в единицах бит) при выполнении задачи. Это было оправдано утверждением, что указание сводится к задаче обработки информации. Хотя не было установлено формальной математической связи между законом Фиттса и теоремой Шеннона-Хартли, которая его вдохновила, форма закона Шеннона широко использовалась, вероятно, из-за привлекательности количественной оценки двигательных действий с использованием теории информации. ^[17] В 2002 году был опубликован стандарт ISO 9241 , предоставляющий стандарты для тестирования интерфейса человек-компьютер, включая использование формы закона Фиттса Шеннона. Было показано, что информация, передаваемая посредством последовательных нажатий клавиш на клавиатуре, и информация, подразумеваемая идентификатором для такой задачи, не согласованы. ^[18] Энтропия Шеннона приводит к иному значению информации, чем закон Фиттса. Однако авторы отмечают, что эта ошибка незначительна и ее следует учитывать только при сравнении устройств с известной энтропией или при измерениях возможностей человека по обработке информации.

Важное усовершенствование закона Фиттса было предложено Кроссманом в 1956 году (см. Welford, 1968, стр. 147–148) ^[19] и использовано Фиттсом в его статье 1964 года с Петерсоном. ^[20] С корректировкой ширина цели ( W ) заменяется эффективной шириной цели ( _We ) . We _{вычисляется} из стандартного отклонения в координатах выбора, собранных в ходе последовательности испытаний для конкретного состояния DW . Если выборы регистрируются как координаты x вдоль оси приближения к цели, то

$${\displaystyle W_{e}=4,133\times SD_{x}}$$

Это дает

$${\displaystyle {\text{ID}}_{e}=\log _{2}{\Bigg (}{\frac {D}{W_{e}}}+1{\Bigg )}}$$

и, следовательно,

$${\displaystyle {\text{IP}}={\Bigg (}{\frac {ID_{e}}{MT}}{\Bigg )}}$$

Если координаты выбора распределены нормально, W _e охватывает 96% распределения. Если наблюдаемая частота ошибок составила 4% в последовательности испытаний, то W _e = W . Если частота ошибок была больше 4%, W _e > W , а если частота ошибок была меньше 4%, W _e < W . Используя W _e , модель закона Фиттса более точно отражает то, что пользователи фактически делали, а не то, что их просили сделать.

Главное преимущество вычисления IP , как указано выше, заключается в том, что пространственная изменчивость или точность включены в измерение. С поправкой на точность закон Фиттса более точно охватывает компромисс между скоростью и точностью. Уравнения выше появляются в ISO 9241-9 как рекомендуемый метод вычисления пропускной способности .

Вскоре после того, как была предложена оригинальная модель, была предложена 2-факторная вариация на основе интуитивного предположения, что расстояние до цели и ширина оказывают раздельное влияние на время движения. Модель Уэлфорда, предложенная в 1968 году, разделила влияние расстояния до цели и ширины на отдельные термины и обеспечила улучшенную предсказательную силу: ^[19]

$${\displaystyle MT=a+b_{1}\log _{2}(D)+b_{2}\log _{2}(W)}$$

Эта модель имеет дополнительный параметр, поэтому ее точность предсказания нельзя напрямую сравнивать с 1-факторными формами закона Фиттса. Однако вариация модели Уэлфорда, вдохновленная формулировкой Шеннона,

$${\displaystyle MT=a+b_{1}\log _{2}(D+W)+b_{2}\log _{2}(W)=a+b\log _{2}\left({\frac {D+W}{W^{k}}}\right)}$$

Дополнительный параметр k позволяет вводить углы в модель. Теперь можно учитывать положение пользователя. Влияние угла можно взвесить с помощью экспоненты. Это дополнение было введено Коппером и др. в 2010 году. ^[21]

Формула сводится к форме Шеннона при k = 1. Следовательно, эту модель можно напрямую сравнить с формой Шеннона закона Фиттса, используя F-тест вложенных моделей. ^[22] Это сравнение показывает, что форма Шеннона модели Уэлфорда не только лучше предсказывает время движения, но и более надежна, когда коэффициент усиления управления-дисплея (соотношение между, например, движением руки и движением курсора) варьируется. Следовательно, хотя модель Шеннона немного сложнее и менее интуитивна, эмпирически она является лучшей моделью для использования в задачах виртуального указания.

В своей первоначальной форме закон Фиттса должен был применяться только к одномерным задачам. Однако в первоначальных экспериментах требовалось, чтобы испытуемые перемещали стилус (в трех измерениях) между двумя металлическими пластинами на столе, что называлось задачей взаимного постукивания. ^[1] Ширина цели, перпендикулярная направлению движения, была очень большой, чтобы избежать ее значительного влияния на производительность. Основное применение закона Фиттса — это двумерные виртуальные задачи указания на экранах компьютеров, в которых цели имеют ограниченные размеры в обоих измерениях.

Закон Фиттса был распространен на двумерные задачи двумя различными способами. Для навигации, например, по иерархическим выпадающим меню, пользователь должен сгенерировать траекторию с помощью указывающего устройства, ограниченную геометрией меню; для этого приложения был выведен закон рулевого управления Аккота-Чжая .

Для простого указания на цели в двумерном пространстве модель обычно сохраняется как есть, но требует корректировки для захвата геометрии цели и количественной оценки ошибок нацеливания логически последовательным образом. ^{[23] [24]} Для определения размера цели использовались несколько методов: ^[25]

• status quo: горизонтальная ширина цели
• суммарная модель: W равна высоте + ширине
• модель площади: W равна высоте * ширине
• меньшее из модели: W меньшее значение высоты и ширины
• W-модель: W — эффективная ширина в направлении движения.

Хотя W -модель иногда считается самым современным измерением, по-настоящему правильное представление для некруглых целей существенно сложнее, поскольку оно требует вычисления угловой свертки между траекторией указателя и целью ^[26]

Поскольку параметры a и b должны фиксировать время перемещения в потенциально широком диапазоне геометрий задач, они могут служить метрикой производительности для данного интерфейса. При этом необходимо отделить различия между пользователями от различий между интерфейсами. Параметр a обычно положителен и близок к нулю, а иногда игнорируется при характеристике средней производительности, как в оригинальном эксперименте Фиттса. ^[18] Существует несколько методов для определения параметров из экспериментальных данных, и выбор метода является предметом жарких споров, поскольку изменение метода может привести к различиям параметров, которые подавляют основные различия производительности. ^{[27] [28]}

Дополнительным вопросом при характеристике производительности является включение показателя успешности: агрессивный пользователь может достичь более короткого времени движения за счет экспериментальных попыток, в которых цель не достигается. Если последние не включены в модель, то среднее время движения может быть искусственно уменьшено.

Закон Фиттса касается только целей, определенных в пространстве. Однако цель может быть определена исключительно на временной оси, что называется временной целью. Мигающая цель или цель, движущаяся к области выбора, являются примерами временных целей. Подобно пространству, расстояние до цели (т. е. временное расстояние D _t ) и ширина цели (т. е. временная ширина W _t ) могут быть определены и для временных целей. Временное расстояние — это количество времени, которое человек должен ждать появления цели. Временная ширина — это короткий промежуток времени с момента появления цели до ее исчезновения. Например, для мигающей цели D _t можно рассматривать как период мигания, а W _t — как продолжительность мигания. Как и в случае с целями в пространстве, чем больше D _t или меньше W _t , тем сложнее становится выбрать цель.

Задача выбора временной цели называется временным указанием . Модель временного указания была впервые представлена ​​в области взаимодействия человека и компьютера в 2016 году. ^[29] Модель предсказывает частоту ошибок, производительность человека при временном указании, как функцию временного индекса сложности ( ID _t ):

$${\displaystyle {\text{ID}}_{t}=\log _{2}{\Bigg (}{\frac {D_{t}}{W_{t}}}{\Bigg )}}$$

Из следствий закона Фиттса можно вывести множество рекомендаций по дизайну графических интерфейсов . В своей базовой форме закон Фиттса гласит, что цели, которые должен поразить пользователь, должны быть как можно больше. Это выводится из параметра W. Более конкретно, эффективный размер кнопки должен быть как можно больше, то есть ее форма должна быть оптимизирована для направления движения пользователя к цели.

Макеты также должны кластеризовать функции, которые обычно используются друг с другом. Оптимизация параметра D таким образом позволяет сократить время в пути.

Размещение элементов макета на четырех краях экрана позволяет размещать бесконечно большие цели в одном измерении и, следовательно, представляет собой идеальные сценарии. Поскольку указатель всегда останавливается на краю, пользователь может перемещать мышь с максимально возможной скоростью и при этом попадать в цель. Целевая область фактически бесконечно длинна вдоль оси движения. Поэтому это правило называется «Правилом бесконечных краев». Использование этого правила можно увидеть, например, в MacOS , где панель меню всегда размещается на верхнем левом краю экрана вместо рамки окна текущей программы. ^[30]

Этот эффект может быть преувеличен в четырех углах экрана. В этих точках два края сталкиваются и образуют теоретически бесконечно большую кнопку. Microsoft Windows (до Windows 11 ) размещает свою кнопку «Пуск» в нижнем левом углу, а Microsoft Office 2007 использует верхний левый угол для своего меню «Офис». Эти четыре места иногда называют «волшебными углами». ^[31] MacOS размещает кнопку закрытия в верхней левой части окна программы, а строка меню заполняет волшебный угол другой кнопкой.

Пользовательский интерфейс, который позволяет использовать всплывающие меню вместо фиксированных выпадающих меню, сокращает время перемещения для параметра D. Пользователь может продолжить взаимодействие прямо из текущего положения мыши и не должен переходить в другую предустановленную область. Многие операционные системы используют это при отображении контекстных меню правой кнопки мыши. Поскольку меню начинается прямо с пикселя, на который нажал пользователь, этот пиксель называется «магическим» или «основным пикселем». ^[25]

Джеймс Бориц и др. (1991) ^[32] сравнили дизайны радиальных меню . В радиальном меню все элементы находятся на одинаковом расстоянии от главного пикселя. Исследование показывает, что в практических реализациях также необходимо учитывать направление, в котором пользователь должен перемещать мышь. Для правшей выбор самого левого элемента меню был значительно сложнее, чем самого правого. Не было обнаружено никаких различий для переходов от верхних к нижним функциям и наоборот.

• Закон рулевого управления Аккота–Чжая
• Закон Хика
• Укажи и щелкни
• Интерфейс на основе пересечения

• Интерактивная визуализация закона Фиттса с помощью JavaScript и D3 Саймона Валлнера
• Закон Фиттса в Департаменте образования. Проект инфраструктуры образования, поддерживаемый NSF
• Закон Фиттса: моделирование времени движения в HCI
• Библиография исследований закона Фиттса, составленная И. Скоттом Маккензи
• Программное обеспечение Fitts' Law – Бесплатная загрузка от I. Scott MacKenzie
• Тест, разработанный Брюсом Тоньяццини, чтобы дать вам представление о Фиттсе