Кривая рыбы с параметром масштаба a = 1 Рыбья кривая — это эллипсная отрицательная педальная кривая , имеющая форму рыбы . В рыбьей кривой точка педали находится в фокусе для особого случая квадрата эксцентриситета . [1] Параметрические уравнения для рыбьей кривой соответствуют уравнениям связанного эллипса . е 2 = 1 2 {\displaystyle e^{2}={\tfrac {1}{2}}}
Уравнения Для эллипса с параметрическими уравнениями
соответствующая кривая рыбы имеет параметрические уравнения х = а потому что ( т ) , у = а грех ( т ) 2 , {\displaystyle \textstyle {x=a\cos(t),\qquad y={\frac {a\sin(t)}{\sqrt {2}}}},} х = а потому что ( т ) − а грех 2 ( т ) 2 , у = а потому что ( т ) грех ( т ) . {\displaystyle \textstyle {x=a\cos(t)-{\frac {a\sin ^{2}(t)}{\sqrt {2}}},\qquad y=a\cos(t)\sin(t)}.}
Когда начало координат переносится в узел (точку пересечения), декартово уравнение можно записать как: [2] [3] ( 2 х 2 + у 2 ) 2 − 2 2 а х ( 2 х 2 − 3 у 2 ) + 2 а 2 ( у 2 − х 2 ) = 0. {\displaystyle \left(2x^{2}+y^{2}\right)^{2}-2{\sqrt {2}}ax\left(2x^{2}-3y^{2}\right)+2a^{2}\left(y^{2}-x^{2}\right)=0.}
Характеристики
Область Площадь кривой рыбы определяется по формуле:
поэтому площадь хвоста и головы определяется по формуле:
что дает общую площадь рыбы как: [2] А = 1 2 | ∫ ( х у ′ − у х ′ ) г т | = 1 8 а 2 | ∫ [ 3 потому что ( т ) + потому что ( 3 т ) + 2 2 грех 2 ( т ) ] г т | , {\displaystyle {\begin{align}A&={\frac {1}{2}}\left|\int {\left(xy'-yx'\right)dt}\right|\\&={\frac {1}{8}}a^{2}\left|\int {\left[3\cos(t)+\cos(3t)+2{\sqrt {2}}\sin ^{2}(t)\right]dt}\right|,\end{align}}} А Хвост = ( 2 3 − π 4 2 ) а 2 , А Голова = ( 2 3 + π 4 2 ) а 2 , {\displaystyle {\begin{aligned}A_{\text{Хвост}}&=\left({\frac {2}{3}}-{\frac {\pi }{4{\sqrt {2}}}}\right)a^{2},\\A_{\text{Голова}}&=\left({\frac {2}{3}}+{\frac {\pi }{4{\sqrt {2}}}}\right)a^{2},\end{aligned}}} А = 4 3 а 2 . {\displaystyle A={\frac {4}{3}}a^{2}.}
Длина дуги кривой определяется по формуле а 2 ( 1 2 π + 3 ) . {\displaystyle a{\sqrt {2}}\left({\frac {1}{2}}\pi +3\right).}
Кривизна кривой рыбы определяется по формуле:
а тангенциальный угол определяется по формуле:
где — комплексный аргумент. К ( т ) = 2 2 + 3 потому что ( т ) − потому что ( 3 т ) 2 а [ потому что 4 т + грех 2 т + грех 4 т + 2 грех ( т ) грех ( 2 т ) ] 3 2 , {\displaystyle K(t)={\frac {2{\sqrt {2}}+3\cos(t)-\cos(3t)}{2a\left[\cos ^{4}t+\sin ^{2}t+\sin ^{4}t+{\sqrt {2}}\sin(t)\sin(2t)\right]^{\frac {3}{2}}}},} ϕ ( т ) = π − арг ( 2 − 1 − 2 ( 1 + 2 ) е я т − 1 ) , {\displaystyle \phi (t)=\pi -\arg \left({\sqrt {2}}-1-{\frac {2}{\left(1+{\sqrt {2}}\right)e^{it}-1}}\right),} арг ( з ) {\displaystyle \arg(z)}
Ссылки ^ Локвуд, Э. Х. (1957). «Отрицательная педальная кривая эллипса относительно фокуса». Math. Gaz . 41 : 254–257 . doi :10.1017/S0025557200037293. S2CID 125623811. ^ ab Weisstein, Eric W. "Fish Curve". MathWorld . Получено 23 мая 2010 г. ^ Локвуд, Э. Х. (1967). Книга кривых . Кембридж, Англия: Cambridge University Press. стр. 157. 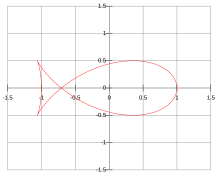




![{\displaystyle {\begin{align}A&={\frac {1}{2}}\left|\int {\left(xy'-yx'\right)dt}\right|\\&={\frac {1}{8}}a^{2}\left|\int {\left[3\cos(t)+\cos(3t)+2{\sqrt {2}}\sin ^{2}(t)\right]dt}\right|,\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937d7b44d8824c63e5f1dd7c5189ca37e53e632f)



![{\displaystyle K(t)={\frac {2{\sqrt {2}}+3\cos(t)-\cos(3t)}{2a\left[\cos ^{4}t+\sin ^{2}t+\sin ^{4}t+{\sqrt {2}}\sin(t)\sin(2t)\right]^{\frac {3}{2}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5edbc1f23fe292015db55bddb719d28ff8415812)

