Фаро тасовать

Вводный раздел этой статьи может быть слишком коротким, чтобы адекватно суммировать основные моменты . Пожалуйста, рассмотрите возможность расширения вводного раздела, чтобы предоставить доступный обзор всех важных аспектов статьи. ( Октябрь 2018 г. )

Тасовка «фаро» (американская), тасовка «вью» (британская) или тасовка «ласточкин хвост» — это метод тасовки игральных карт , при котором половина колоды удерживается в каждой руке большими пальцами внутрь, затем карты отпускаются большими пальцами так, что они падают на стол перемежающимися. Диаконис, Грэхем и Кантор также называют это техникой , когда используют ее в магии. ^[1]

Математики используют термин «перетасовка фаро» для описания точной перестановки колоды в две равные стопки по 26 карт, которые затем идеально чередуются. ^[2]

Правша держит карты сверху в левой руке и снизу в правой руке. Колода делится на две предпочтительно равные части, просто слегка приподнимая половину карт правым большим пальцем и отталкивая пачку левой руки вперед от правой руки. Две пачки часто скрещивают и постукивают друг о друга, чтобы выровнять их. Затем их сталкивают короткими сторонами и сгибают либо вверх, либо вниз. Затем карты поочередно падают друг на друга, в идеале поочередно по одной из каждой половины, как застежка-молния . Можно добавить флориш, соединив пачки вместе, надавив и согнув их сверху. ^[3]

Игра в Фаро заканчивается тем, что карты распределяются по двум равным стопкам, которые дилер должен объединить, чтобы сдать их для следующей игры. По словам фокусника Джона Маскелайна , использовался вышеуказанный метод, и он называет его «перетасовкой дилера Фаро». ^[4] Маскелайн был первым, кто дал четкие инструкции, но перетасовка использовалась и ассоциировалась с Фаро ранее, как было обнаружено в основном математиком и фокусником Перси Диаконисом . ^[5]

Тасовка «Фаро» — это контролируемая тасовка, которая не полностью рандомизирует колоду.

Для идеальной тасовки фаро, когда карты идеально чередуются, тасовщику необходимо разделить колоду на две равные стопки и приложить необходимое усилие, вдавливая половинки колоды друг в друга.

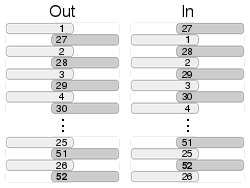
Тасовка фаро, при которой исходная верхняя карта остается наверху, а исходная нижняя карта — внизу, называется « out-shuffle» , а тасовка, при которой исходная верхняя карта перемещается на вторую, а исходная нижняя карта — на вторую снизу, называется « in-shuffle» . Эти названия придумал фокусник и программист Алекс Элмсли . ^[6]

Тасовка out-shuffle имеет тот же результат, что и удаление верхней и нижней карт, выполнение in-shuffle на оставшихся картах, а затем возвращение верхней и нижней карт на их исходные позиции. Повторные out-shuffle не могут изменить порядок всей колоды, только средних n−2 карт. Математические теоремы относительно тасовок фаро, как правило, относятся к out-shuffle.

Тасовка в колоде имеет тот же результат, что и добавление одной лишней карты сверху и одной лишней карты снизу, выполнение тасовки наружу на увеличенной колоде, а затем удаление лишних карт. Повторные тасовки в колоде могут поменять порядок колоды на обратный.

Если кто-то может делать идеальные тасовки, то 26 тасовок изменят порядок колоды на обратный, а еще 26 — восстановят ее в первоначальном порядке. ^[7]

В общем случае, идеальные тасовки восстановят порядок колоды из -карт, если . Например, 52 последовательных тасовки восстановят порядок колоды из 52 карт, потому что .${\displaystyle к}$${\displaystyle n}$${\displaystyle 2^{k}\equiv 1{\pmod {n+1}}}$${\displaystyle 2^{52}\equiv 1{\pmod {53}}}$

В общем случае, идеальные перетасовки восстановят порядок колоды из -карт, если . Например, если удастся выполнить восемь перетасовок подряд, то колода из 52 карт будет восстановлена ​​в своем первоначальном порядке, потому что . Однако для восстановления порядка колоды из 64 карт требуется всего 6 перетасовок фаро.${\displaystyle к}$${\displaystyle n}$${\displaystyle 2^{k}\equiv 1{\pmod {n-1}}}$${\displaystyle 2^{8}\equiv 1{\pmod {51}}}$

Другими словами, количество перетасовок, необходимых для возврата колоды карт четного размера n в исходный порядок, определяется мультипликативным порядком 2 по модулю ( n  + 1).

Например, для колоды размером n = 2, 4, 6, 8, 10, 12 ..., необходимое количество тасовок составит: 2, 4, 3, 6, 10, 12, 4, 8, 18, 6, 11, ... (последовательность A002326 в OEIS ).

Согласно гипотезе Артина о примитивных корнях , существует бесконечно много размеров колод, требующих полного набора из n перетасовок. ^[8]

Аналогичная операция перетасовки для бесконечной последовательности — перемежение последовательности .

Для простоты мы будем использовать колоду из шести карт.

Ниже показан порядок колоды после каждой перетасовки. Колода такого размера возвращается к своему первоначальному порядку после 3 перетасовок.

Шаг	Верхняя карта	2	3	4	5	Нижняя карта
Начинать
1
2
3

Ниже показан порядок колоды после каждой перетасовки. Колода такого размера возвращается к своему первоначальному порядку после 4 перетасовок.

Шаг	Верхняя карта	2	3	4	5	Нижняя карта
Начинать
1
2
3
4

Фокусник Алекс Элмсли обнаружил ^{[ нужна цитата ]} , что контролируемая серия тасовок внутрь и наружу может использоваться для перемещения верхней карты колоды вниз в любую желаемую позицию. Фокус в том, чтобы выразить желаемую позицию карты как двоичное число , а затем сделать тасовку внутрь для каждой 1 и тасовку наружу для каждого 0.

Например, чтобы переместить верхнюю карту вниз так, чтобы над ней было десять карт, выразите число десять в двоичной системе (1010 ₂ ). Перетасуйте, перетасуйте, перетасуйте, перетасуйте. Сдайте десять карт сверху колоды; одиннадцатая будет вашей исходной картой. Обратите внимание, что неважно, выразите ли вы число десять как 1010 ₂ или 00001010 ₂ ; предварительные перетасовки не повлияют на результат, потому что перетасовки всегда оставляют верхнюю карту наверху.

В математике идеальную тасовку можно считать элементом симметрической группы .

В более общем смысле , идеальная перетасовка — это перестановка, которая разделяет набор на две стопки и чередует их:${\displaystyle S_{2n}}$

${\displaystyle S_{2n}}$=${\displaystyle {\begin{pmatrix}1&2&3&4&\cdots &2n-1&2n\\1&n+1&2&n+2&\cdots &n&2n\end{pmatrix}}}$

Другими словами, это карта.

${\displaystyle k\mapsto {\begin{cases}{\frac {k+1}{2}}&k\ {\text{нечетный}}\\n+{\frac {k}{2}}&k\ {\text{четный}}\end{cases}}}$

Аналогично, -совершенная перестановка ^[9] — это элемент , который разбивает набор на k стопок и чередует их.${\displaystyle (к,н)}$${\displaystyle S_{кн}}$

Идеальная тасовка, обозначаемая , представляет собой композицию идеальной тасовки с циклом , поэтому знак имеет вид:${\displaystyle (2,n)}$${\displaystyle \rho _{n}}$${\displaystyle (2,n-1)}$${\displaystyle n}$${\displaystyle \rho _{n}}$

${\displaystyle {\mbox{sgn}}(\rho _{n})=(-1)^{n+1}{\mbox{sgn}}(\rho _{n-1}).}$

Таким образом, знак является 4-периодическим:

${\displaystyle {\mbox{sgn}}(\rho _{n})=(-1)^{\lfloor n/2\rfloor }={\begin{cases}+1&n\equiv 0,1{\pmod {4}}\\-1&n\equiv 2,3{\pmod {4}}\end{cases}}}$

Первые несколько идеальных перетасовок: и тривиальны, а — это транспозиция .${\displaystyle \rho _{0}}$${\displaystyle \rho _{1}}$${\displaystyle \rho _{2}}$${\displaystyle (23)\in S_{4}}$

• Диаконис, Персия ; Грэм, РЛ ; Кантор, WM (1983). «Математика идеальных тасовок» (PDF) . Достижения прикладной математики . 4 (2): 175–196. дои : 10.1016/0196-8858(83)90009-X .

• Эллис, Дж.; Фань, Х.; Шаллит, Дж. (2002). «Циклы многоходовой идеальной перестановки» (PDF) . Дискретная математика и теоретическая информатика . 5 : 169–180. doi :10.46298/dmtcs.308 . Получено 26 декабря 2013 г. .

• Maskelyne, John (1894). Sharps and Flats: A Complete Revelation of the Secrets of Cheating at Games of Chance and Skill. Longmans, Green and Company . Получено 26 декабря 2013 г.

• Моррис, С. Брент (1998). Волшебные трюки, тасование карт и динамическая компьютерная память. Математическая ассоциация Америки. ISBN 0-883-85527-5. Получено 26 декабря 2013 г.

• Колата, Джина (апрель 1982 г.). «Идеальные перетасовки и их связь с математикой». Science . 216 (4545): 505–506. Bibcode :1982Sci...216..505K. doi :10.1126/science.216.4545.505. PMID  17735734.

• Джейн, Пейюш (май 2008 г.). «Простой алгоритм на месте для перемешивания». arXiv : 0805.1598 [cs.DS].