Злое число

зло	отвратительный
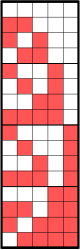
Первые 16 злых и одиозных чисел в двоичной системе счисления little- endian . Видно, что обе последовательности отличаются только младшими битами, которые образуют последовательность Туэ–Морса для злых чисел и ее отрицание для одиозных чисел. Остальные биты образуют четные числа.

В теории чисел злое число — это неотрицательное целое число, которое имеет четное количество единиц в своем двоичном разложении . ^[1] Эти числа задают позиции нулевых значений в последовательности Туэ–Морса , и по этой причине их также называют множеством Туэ–Морса . ^[2] Неотрицательные целые числа, которые не являются злыми, называются одиозными числами .

Первые злые числа:

0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, 39... ^[1]

Разбиение неотрицательных целых чисел на одиозные и злые числа — это единственное разбиение этих чисел на два множества, имеющих равные мультимножества попарных сумм. ^[3]

Как показал математик 19 века Эжен Пруэ, разбиение на злые и отвратительные числа чисел от до для любого даёт решение задачи Пруэ–Тэрри–Эскотта о нахождении множеств чисел, суммы степеней которых равны вплоть до -й степени. ^[4]${\displaystyle 0}$${\displaystyle 2^{k}-1}$${\displaystyle к}$${\displaystyle к}$

В информатике говорят, что злое число имеет четную четность .