Код стирания
В теории кодирования код со стиранием — это код с прямой коррекцией ошибок (FEC) в предположении стирания битов (а не ошибок битов), который преобразует сообщение из k символов в более длинное сообщение (кодовое слово) с n символами, так что исходное сообщение может быть восстановлено из подмножества из n символов. Дробь r = k / n называется скоростью кода . Дробь k'/k , где k' обозначает количество символов, необходимых для восстановления, называется эффективностью приема. Алгоритм восстановления ожидает, что известно, какие из n символов потеряны.
История
Стирающее кодирование было изобретено Ирвингом Ридом и Гюставом Соломоном в 1960 году. [1]
Существует множество различных схем кодирования стирания. Наиболее популярными кодами стирания являются кодирование Рида-Соломона , коды с низкой плотностью проверки на четность (LDPC-коды) и турбо-коды . [1]
По состоянию на 2023 год современные системы хранения данных могут быть спроектированы так, чтобы выдерживать полный отказ нескольких дисков без потери данных, используя один из 3 подходов: [2] [3] [4]
- Репликация
- РЕЙД
- Кодирование стирания
Хотя технически RAID можно рассматривать как своего рода код стирания, [5] «RAID» обычно применяется к массиву, подключенному к одному хост-компьютеру (который является единой точкой отказа), в то время как «кодирование стирания» обычно подразумевает несколько хостов, [3] иногда называемых избыточным массивом недорогих серверов (RAIS). Код стирания позволяет продолжать операции, когда любой из этих хостов останавливается. [4] [6]
По сравнению с системами RAID на уровне блоков кодирование стирания объектного хранилища имеет некоторые существенные отличия, которые делают его более устойчивым. [7] [8] [9] [10] [11]
Оптимальные коды стирания
Этот раздел может быть слишком техническим для понимания большинства читателей . ( Август 2023 ) |
Оптимальные коды стирания обладают тем свойством, что любые k из n символов кодового слова достаточны для восстановления исходного сообщения (т.е. они имеют оптимальную эффективность приема). Оптимальные коды стирания являются кодами с максимальным расстоянием разделения (коды MDS).
Проверка четности
Проверка четности — это особый случай, когда n = k + 1. Из набора k значений вычисляется контрольная сумма, которая добавляется к k исходным значениям:
Набор значений k + 1 теперь согласован относительно контрольной суммы. Если одно из этих значений, , стерто, его можно легко восстановить, суммируя оставшиеся переменные:
RAID 5 — это широко используемое применение кода стирания с проверкой четности. [1]
Полиномиальная передискретизация
Пример: Err-mail (к = 2)
В простом случае, когда k = 2, символы избыточности могут быть созданы путем выборки различных точек вдоль линии между двумя исходными символами. Это показано на простом примере, называемом err-mail:
Алиса хочет отправить свой номер телефона (555629) Бобу с помощью err-mail. Err-mail работает так же, как электронная почта, за исключением того,
- Около половины всей почты теряется.
- Сообщения длиннее 5 символов являются незаконными.
- Это очень дорого (аналогично авиапочте).
Вместо того чтобы просить Боба подтверждать получение сообщений, которые она отправляет, Алиса придумывает следующую схему.
- Она разбивает свой номер телефона на две части a = 555, b = 629 и отправляет Бобу два сообщения: «A=555» и «B=629».
- Она строит линейную функцию, в данном случае , такую, что и .
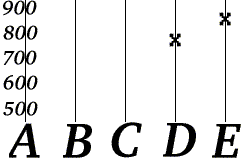
- Она вычисляет значения f (3), f (4) и f (5), а затем передает три избыточных сообщения: «C=703», «D=777» и «E=851».
Боб знает, что форма f ( k ) — это , где a и b — две части телефонного номера. Теперь предположим, что Боб получает «D=777» и «E=851».
Боб может восстановить номер телефона Алисы, вычислив значения a и b из значений ( f (4) и f (5)), которые он получил. Боб может выполнить эту процедуру, используя любые два сообщения об ошибке, поэтому код стирания в этом примере имеет скорость 40%.
Обратите внимание, что Алиса не может закодировать свой номер телефона всего в одном сообщении err-mail, поскольку оно содержит шесть символов, а максимальная длина одного сообщения err-mail составляет пять символов. Если бы она отправляла свой номер телефона частями, прося Боба подтвердить получение каждой части, в любом случае пришлось бы отправить не менее четырех сообщений (два от Алисы и два подтверждения от Боба). Поэтому код стирания в этом примере, требующий пяти сообщений, довольно экономичен.
Этот пример немного надуман. Для действительно универсальных кодов стирания, которые работают с любым набором данных, нам понадобится что-то другое, чем f ( i ), указанное выше.
Общий случай
Линейную конструкцию выше можно обобщить до полиномиальной интерполяции . Кроме того, теперь точки вычисляются над конечным полем .
Сначала мы выбираем конечное поле F с порядком не менее n , но обычно степенью 2. Отправитель нумерует символы данных от 0 до k − 1 и отправляет их. Затем он строит (Лагранжев) полином p ( x ) порядка k такой, что p ( i ) равен символу данных i . Затем он отправляет p ( k ), ..., p ( n − 1). Теперь получатель также может использовать полиномиальную интерполяцию для восстановления потерянных пакетов, при условии, что он успешно получит k символов. Если порядок F меньше 2 b , где b — количество бит в символе, то можно использовать несколько полиномов.
Отправитель может построить символы от k до n − 1 «на лету», т. е. равномерно распределить рабочую нагрузку между передачей символов. Если получатель хочет выполнить свои вычисления «на лету», он может построить новый полином q , такой, что q ( i ) = p ( i ), если символ i < k был получен успешно, и q ( i ) = 0, когда символ i < k не был получен. Теперь пусть r ( i ) = p ( i ) − q ( i ). Во-первых, мы знаем, что r ( i ) = 0, если символ i < k был получен успешно. Во-вторых, если символ i ≥ k был получен успешно, то можно вычислить r ( i ) = p ( i ) − q ( i ). Таким образом, у нас достаточно точек данных, чтобы построить r и оценить его, чтобы найти потерянные пакеты. Таким образом, и отправителю, и получателю требуется O ( n ( n − k )) операций и только O ( n − k ) памяти для работы «на лету».
Реализация в реальном мире
Этот процесс реализуется с помощью кодов Рида–Соломона , в которых кодовые слова строятся над конечным полем с использованием матрицы Вандермонда .
Большинство практичных кодов стирания являются систематическими кодами — каждый из исходных k символов может быть найден скопированным, незакодированным, как один из n символов сообщения. [12] (Коды стирания, которые поддерживают разделение секрета, никогда не используют систематический код).
Почти оптимальные коды стирания
Почти оптимальные коды стирания требуют (1 + ε) k символов для восстановления сообщения (где ε>0). Уменьшение ε может быть достигнуто за счет процессорного времени. Почти оптимальные коды стирания жертвуют возможностями коррекции ради вычислительной сложности: практические алгоритмы могут кодировать и декодировать с линейной временной сложностью.
Фонтанные коды (также известные как коды стирания без скорости ) являются яркими примерами кодов стирания, близких к оптимальным . Они могут преобразовать сообщение из k символов в практически бесконечную закодированную форму, т. е. они могут генерировать произвольное количество избыточных символов, которые могут быть использованы для исправления ошибок. Приемники могут начать декодирование после того, как получат немного больше k закодированных символов.
Регенерация кодов решает проблему восстановления (также называемого восстановлением) потерянных закодированных фрагментов из существующих закодированных фрагментов. Эта проблема возникает в распределенных системах хранения, где связь для поддержания закодированной избыточности является проблемой. [12]
Применение стирающего кодирования в системах хранения данных
Стирающее кодирование теперь является стандартной практикой для надежного хранения данных. [13] [14] [15] В частности, различные реализации стирающего кодирования Рида-Соломона используются Apache Hadoop , RAID-6, встроенным в Linux, Microsoft Azure, холодным хранилищем Facebook и Backblaze Vaults. [15] [12]
Классический способ восстановления после сбоев в системах хранения данных — репликация. Однако репликация влечет за собой значительные накладные расходы в виде потерянных байтов. Поэтому все более крупные системы хранения данных, такие как те, что используются в центрах обработки данных, используют хранилище с кодированием стирания. Наиболее распространенной формой кодирования стирания, используемой в системах хранения данных, является код Рида-Соломона (RS) , передовая математическая формула, используемая для восстановления недостающих данных из фрагментов известных данных, называемых блоками четности. В коде RS ( k , m ) заданный набор из k блоков данных, называемых «фрагментами», кодируется в ( k + m ) фрагментов. Общий набор фрагментов составляет полосу . Кодирование выполняется таким образом, что пока доступно по крайней мере k из ( k + m ) фрагментов, можно восстановить все данные. Это означает, что хранилище с кодированием RS ( k , m ) может выдерживать до m сбоев.
Пример: В коде RS (10, 4), который используется в Facebook для их HDFS , [16] 10 МБ пользовательских данных делятся на десять блоков по 1 МБ. Затем создаются четыре дополнительных блока четности по 1 МБ для обеспечения избыточности. Это может выдержать до 4 одновременных сбоев. Накладные расходы на хранение здесь составляют 14/10 = 1,4X.
В случае полностью реплицированной системы 10 МБ пользовательских данных придется реплицировать 4 раза, чтобы выдержать до 4 одновременных сбоев. Накладные расходы на хранение в этом случае составят 50/10 = 5 раз.
Это дает представление о меньших накладных расходах на хранение данных с кодированием стиранием по сравнению с полной репликацией и, следовательно, о привлекательности современных систем хранения данных.
Первоначально коды стирания использовались для снижения стоимости эффективного хранения «холодных» (редко используемых) данных; но коды стирания могут также использоваться для повышения производительности обслуживания «горячих» (чаще используемых) данных. [12]
RAID N+M разделяет блоки данных между N+M дисками и может восстановить все данные при выходе из строя любого из M дисков. [1] В частности, RAID 7.3 относится к RAID с тройной четностью и может восстановить все данные при выходе из строя любых 3 дисков. [17]
Примеры
Вот несколько примеров реализации различных кодов:
Почти оптимальные коды стирания
Почти оптимальные фонтанные коды (стирание без скорости)
Оптимальные коды стирания
- Четность : используется в системах хранения RAID .
- Parchive
- Tahoe-LAFS включает zfec
- Коды Рида–Соломона
- Erasure Resilient Systematic Code, MDS-код, превосходящий код Рида-Соломона по максимальному количеству избыточных пакетов, [ по чьему мнению? ] см. RS(4,2) с 2 битами или RS(9,2) с 3 битами
- Регенерация кодов [18] [19]
- любой другой максимально разделяемый код
Смотрите также
- Коды прямого исправления ошибок .
- Разделение секрета (отличается тем, что исходный секрет шифруется и скрывается до тех пор, пока не будет достигнут кворум декодирования)
- Орфографический алфавит
- Двоичный канал стирания
Ссылки
- ^ abcd "RAID против Erasure Coding. В чем разница? | Блог | Xinnor". Самый быстрый и надежный программный RAID | Xinnor . 2023-09-03 . Получено 2024-09-18 .
- ^ "Ceph.io — Стирающее кодирование в Ceph". ceph.io . 2014-04-07 . Получено 2024-09-18 .
- ^ ab Lee, Brandon (2023-12-26). "RAID против стирающего кодирования против репликации". BDRSuite . Получено 2024-09-18 .
- ^ ab O'Reilly, Jim. "RAID против стирающего кодирования". www.networkcomputing.com . Получено 18 сентября 2024 г.
- ^ Димитрий Пертин, Александр ван Кемпен, Бенуа Паррен, Николя Норман. "Сравнение кодов стирания RAID-6". Третий китайско-французский семинар по информационным и коммуникационным технологиям, SIFWICT 2015, июнь 2015, Нант, Франция. ffhal-01162047f
- ^ "Понимание отказоустойчивости IBM Spectrum Scale Erasure Code Edition". www.ibm.com . Получено 2024-09-18 .
- ^ "Стирающее кодирование объектного хранилища против RAID-массива блочного хранилища". Блог MinIO . 2021-07-27 . Получено 2024-09-18 .
- ^ "Erasure coding vs Raid как метод защиты данных | Computer Weekly". ComputerWeekly.com . Получено 2024-09-18 .
- ^ Крут, Питер (2023-10-04). "Erasure Code: RAID As It Should Be – Huawei BLOG". Архивировано из оригинала 2023-10-04 . Получено 2024-09-18 .
- ^ "Erasure Coding 101". Блог MinIO . 2022-04-25 . Получено 2024-09-18 .
- ^ Бхаскаран, Динеш Кумар (6 июля 2018 г.). «Почему стирающее кодирование — будущее устойчивости данных». Архивировано из оригинала 7 августа 2020 г.
- ^ abcd Рашми Винаяк. «Стирающее кодирование для систем больших данных: теория и практика». 2016. стр. 2: раздел «Аннотация». стр. 9: раздел «Систематические коды». стр. 12: раздел «Регенерирующие коды».
- ^ «Кодирование со стиранием — практика и принципы». 2016.
- ^ Мэтт Саррел. «Erasure Coding 101». 2022.
- ^ Брайан Бич. «Исходный код Backblaze с открытым исходным кодом стирания Рида-Соломона». 2015.
- ^ Ся, Минюань; Саксена, Мохит; Блаум, Марио; Пиз, Дэвид А. (2015). История двух кодов стирания в {HDFS}. стр. 213–226 . ISBN 978-1-931971-20-1.
- ^ Адам Левенталь. ""Тройной RAID и далее". 2009.
- ^ Dimakis, Alexandros G.; Godfrey, P. Brighten; Wu, Yunnan; Wainwright, Martin J.; Ramchandran, Kannan (сентябрь 2010 г.). «Сетевое кодирование для распределенных систем хранения данных». Труды IEEE по теории информации . 56 (9): 4539– 4551. arXiv : cs/0702015 . CiteSeerX 10.1.1.117.6892 . doi :10.1109/TIT.2010.2054295. S2CID 260559901.
- ^ "home [Erasure Coding for Distributed Storage Wiki]". 2017-07-31. Архивировано из оригинала 2017-07-31 . Получено 2023-08-20 .
Внешние ссылки
- Jerasure — это библиотека свободного программного обеспечения, реализующая методы стирания кода Рида-Соломона и Коши с оптимизацией SIMD.
- Программное обеспечение FEC в компьютерных коммуникациях Луиджи Риццо описывает оптимальные коды исправления стирания
- Feclib — это почти оптимальное расширение работы Луиджи Риццо, использующее ленточные матрицы. Можно задать множество параметров, например, размер ширины полосы и размер конечного поля. Он также успешно использует большой размер регистра современных ЦП. Неизвестно, как он соотносится с почти оптимальными кодами, упомянутыми выше.
- Википедия по кодированию распределенных хранилищ для регенерации кодов и восстановления кодов стирания.
- ECIP "Erasure Code Internet Protocol" Разработанный в 1996 году, был первым применением FEC "Forward Error Correction" в Интернете. Впервые он был использован в коммерческих целях для *трансляции живого видео сэра Артура Кларка в Шри-Ланке в UIUC в Индиане.