Математическое моделирование инфекционных заболеваний
Использование математических моделей для понимания путей передачи инфекционных заболеваний

Математические модели могут прогнозировать, как инфекционные заболевания прогрессируют, чтобы показать вероятный исход эпидемии ( в том числе среди растений ) и помочь информировать общественное здравоохранение и вмешательства в здоровье растений. Модели используют основные предположения или собранные статистические данные вместе с математикой, чтобы найти параметры для различных инфекционных заболеваний и использовать эти параметры для расчета эффектов различных вмешательств, таких как программы массовой вакцинации . Моделирование может помочь решить, какие вмешательства следует избегать, а какие следует опробовать, или может предсказать будущие модели роста и т. д.

История

Моделирование инфекционных заболеваний — это инструмент, который использовался для изучения механизмов распространения заболеваний, прогнозирования будущего течения вспышки и оценки стратегий борьбы с эпидемией. [1]

Первым ученым, который систематически пытался количественно оценить причины смерти, был Джон Граунт в своей книге « Естественные и политические наблюдения, сделанные над счетами смертности » в 1662 году. Счета, которые он изучал, представляли собой списки цифр и причин смерти, публиковавшиеся еженедельно. Анализ Граунтом причин смерти считается началом «теории конкурирующих рисков», которая, по словам Дейли и Гани [1] , является «теорией, которая в настоящее время прочно укоренилась среди современных эпидемиологов».

Самый ранний отчет о математическом моделировании распространения болезней был выполнен в 1760 году Даниилом Бернулли . Получив медицинское образование, Бернулли создал математическую модель для защиты практики прививок от оспы . [2] Расчеты по этой модели показали, что всеобщая прививка от оспы увеличит продолжительность жизни с 26 лет 7 месяцев до 29 лет 9 месяцев. [3] Работа Даниила Бернулли предшествовала современному пониманию теории микробов . [4]

В начале 20 века Уильям Хамер [5] и Рональд Росс [6] применили закон действия масс для объяснения поведения эпидемий.

В 1920-х годах появились компартментальные модели. Модель эпидемии Кермака-Маккендрика (1927) и модель эпидемии Рида-Фроста (1928) описывают взаимосвязь между восприимчивыми , инфицированными и иммунными лицами в популяции. Модель эпидемии Кермака-Маккендрика успешно предсказывала поведение вспышек, очень похожее на то, что наблюдалось во многих зарегистрированных эпидемиях. [7]

В последнее время агентные модели (ABM) используются вместо более простых компартментальных моделей . [8] Например, эпидемиологические ABM используются для информирования о вмешательствах в здравоохранение (нефармацевтических) против распространения SARS-CoV-2 . [9] Эпидемиологические ABM, несмотря на их сложность и необходимость высокой вычислительной мощности, подвергаются критике за упрощение и нереалистичные предположения. [10] [11] Тем не менее, они могут быть полезны для информирования о решениях относительно мер смягчения и подавления в случаях, когда ABM точно откалиброваны. [12]

Предположения

Модели хороши ровно настолько, насколько хороши предположения, на которых они основаны. Если модель делает прогнозы, которые не соответствуют наблюдаемым результатам, а математика верна, то первоначальные предположения должны быть изменены, чтобы сделать модель полезной. [13]

  • Прямоугольное и стационарное распределение возраста , т. е. все в популяции доживают до возраста L , а затем умирают, и для каждого возраста (до L ) в популяции одинаковое количество людей. Это часто вполне оправдано для развитых стран, где низкая детская смертность и большая часть населения доживает до ожидаемой продолжительности жизни.
  • Однородное смешивание населения, т. е. индивиды изучаемого населения подбираются и вступают в контакт случайным образом и не смешиваются в основном в более мелкой подгруппе. Это предположение редко оправдывается, поскольку социальная структура широко распространена. Например, большинство людей в Лондоне вступают в контакт только с другими лондонцами. Кроме того, в Лондоне существуют более мелкие подгруппы, такие как турецкая община или подростки (просто чтобы привести два примера), которые смешиваются друг с другом больше, чем люди вне их группы. Однако однородное смешивание является стандартным предположением, чтобы сделать математику поддающейся обработке.

Типы моделей эпидемий

Стохастический

«Стохастический» означает быть или иметь случайную величину. Стохастическая модель — это инструмент для оценки вероятностных распределений потенциальных результатов, допускающий случайные вариации в одном или нескольких входных данных с течением времени. Стохастические модели зависят от случайных вариаций в риске воздействия, заболевании и другой динамике болезни. Статистическое распространение болезни на уровне агента в малых или больших популяциях может быть определено стохастическими методами. [14] [15] [16]

Детерминированный

При работе с большими группами населения, как в случае туберкулеза, часто используются детерминированные или компартментальные математические модели. В детерминированной модели индивидуумы в популяции распределяются по разным подгруппам или компартментам, каждый из которых представляет определенную стадию эпидемии. [17]

Скорость перехода из одного класса в другой математически выражается как производные, поэтому модель формулируется с использованием дифференциальных уравнений. При построении таких моделей необходимо предполагать, что численность популяции в отсеке дифференцируема по времени и что эпидемический процесс является детерминированным. Другими словами, изменения в популяции отсека можно рассчитать, используя только историю, которая использовалась для разработки модели. [7]

Кинетика и среднее поле

Формально эти модели относятся к классу детерминированных моделей; однако они включают в динамику гетерогенные социальные характеристики, такие как уровни социальности, мнения, благосостояния, географическое положение индивидуумов, которые глубоко влияют на распространение болезни. Эти модели обычно представлены частными дифференциальными уравнениями, в отличие от классических моделей, описываемых как системы обыкновенных дифференциальных уравнений. Следуя принципам вывода кинетической теории, они дают более строгое описание динамики эпидемии, начиная с агентных взаимодействий. [18]

Субэкспоненциальный рост

Распространенное объяснение роста эпидемий заключается в том, что 1 человек заражает 2, те 2 заражают 4 и так далее и так далее, причем число инфицированных удваивается с каждым поколением. Это аналогично игре в пятнашки , где 1 человек помечает 2, те 2 помечают 4 других, которые никогда не были помечены, и так далее. По мере развития этой игры она становится все более безумной, поскольку помеченные пробегают мимо ранее помеченных, чтобы выследить тех, кто никогда не был помечен. Таким образом, эта модель эпидемии приводит к кривой, которая растет экспоненциально, пока не рухнет до нуля, поскольку все население инфицировано. т.е. никакого коллективного иммунитета и никакого пика и постепенного спада, как это наблюдается в реальности. [19]

Модели эпидемий в сетях

Эпидемии можно моделировать как заболевания, распространяющиеся по сетям контактов между людьми. Такая сеть может быть представлена ​​математически с помощью графа и называется контактной сетью. [20] Каждый узел в контактной сети является представлением индивидуума, а каждая связь (ребро) между парой узлов представляет контакт между ними. Связи в контактных сетях могут использоваться для передачи заболевания между индивидуумами, и каждое заболевание имеет свою собственную динамику поверх своей контактной сети. Сочетание динамики заболевания под влиянием вмешательств, если таковые имеются, на контактной сети может быть смоделировано с помощью другой сети, известной как сеть передачи. В сети передачи все связи отвечают за передачу заболевания. Если такая сеть является локально древовидной сетью, то есть любое локальное соседство в такой сети принимает форму дерева , то базовое воспроизведение может быть записано в терминах средней степени избыточности сети передачи, такой что:

Р 0 = ⟨ к 2 ⟩ ⟨ к ⟩ − 1 , {\displaystyle R_{0}={\frac {\langle k^{2}\rangle {\langle k\rangle }}-1,}

где — средняя степень (средняя степень) сети, а — второй момент распределения степеней сети передачи . Однако не всегда просто найти сеть передачи из контактной сети и динамики заболевания. [21] Например, если контактную сеть можно аппроксимировать графом Эрдеша–Реньи с пуассоновским распределением степеней , а параметры распространения заболевания определены в приведенном выше примере, например, — скорость передачи на человека, а средний инфекционный период заболевания равен , то базовое число воспроизводства равно [22] [23], поскольку для распределения Пуассона. 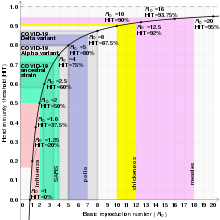⟨ к ⟩ {\displaystyle {\langle k\rangle}} ⟨ к 2 ⟩ {\displaystyle {\langle k^{2}\rangle }} β {\displaystyle \бета} 1 γ {\displaystyle {\dfrac {1}{\gamma }}} Р 0 = β γ ⟨ к ⟩ {\displaystyle R_{0}={\dfrac {\beta }{\gamma }}{\langle k\rangle }} ⟨ к 2 ⟩ − ⟨ к ⟩ 2 = ⟨ к ⟩ {\displaystyle {\langle k^{2}\rangle }-{\langle k\rangle }^{2} = {\langle k\rangle }}

Номер репродукции

Базовое репродуктивное число (обозначаемое как R 0 ) является мерой того, насколько передается болезнь. Это среднее число людей, которых один заразный человек заразит в течение своей инфекции. Это количество определяет, будет ли инфекция увеличиваться субэкспоненциально , вымрет или останется постоянной: если R 0 > 1, то каждый человек в среднем заражает более одного другого человека, поэтому болезнь будет распространяться; если R 0 < 1, то каждый человек в среднем заражает менее одного человека, поэтому болезнь вымрет; и если R 0 = 1, то каждый человек в среднем заразит ровно одного другого человека, поэтому болезнь станет эндемичной: она будет распространяться по всей популяции, но не увеличится и не уменьшится. [24]

Эндемическое устойчивое состояние

Инфекционное заболевание считается эндемичным , когда оно может поддерживаться в популяции без необходимости внешнего воздействия. Это означает, что в среднем каждый инфицированный человек заражает ровно одного другого человека (если больше, то число инфицированных людей будет расти субэкспоненциально , и начнется эпидемия , если меньше, то болезнь исчезнет). В математических терминах это:

  Р 0 С   = 1. {\displaystyle \ R_{0}S\ =1.}

Базовое репродуктивное число ( R 0 ) заболевания, предполагая, что все восприимчивы, умноженное на долю населения, которое фактически восприимчиво ( S ), должно быть равно единице (поскольку те, кто не восприимчив, не фигурируют в наших расчетах, поскольку они не могут заразиться болезнью). Обратите внимание, что это соотношение означает, что для того, чтобы заболевание находилось в эндемическом устойчивом состоянии , чем выше базовое репродуктивное число, тем ниже должна быть доля восприимчивой популяции, и наоборот. Это выражение имеет ограничения, касающиеся доли восприимчивости, например, R 0 равно 0,5, подразумевает, что S должно быть равно 2, однако эта доля превышает размер популяции. [ необходима цитата ]

Предположим, что распределение возраста прямоугольное, а возраст инфицирования имеет такое же распределение для каждого года рождения. Пусть средний возраст инфицирования будет A , например, когда индивидуумы моложе A восприимчивы, а те, кто старше A, иммунны (или заразны). Тогда можно показать простым рассуждением, что доля популяции, которая восприимчива, определяется как:

С = А Л . {\displaystyle S={\frac {A}{L}}.}

Мы повторяем, что L — это возраст, в котором в этой модели предполагается, что каждый индивидуум умрет. Но математическое определение эндемичного устойчивого состояния можно переформулировать так:

С = 1 Р 0 . {\displaystyle S={\frac {1}{R_{0}}}.}

Поэтому, в силу транзитивного свойства :

1 Р 0 = А Л ⇒ Р 0 = Л А . {\displaystyle {\frac {1}{R_{0}}}={\frac {A}{L}}\Rightarrow R_{0}={\frac {L}{A}}.}

Это обеспечивает простой способ оценки параметра R0 с использованием легкодоступных данных.

Для популяции с экспоненциальным распределением возраста ,

Р 0 = 1 + Л А . {\displaystyle R_{0}=1+{\frac {L}{A}}.}

Это позволяет определить базовое репродуктивное число заболевания с учетом A и L в любом типе распределения популяции.

Компартментальные модели в эпидемиологии

Компартментальные модели формулируются как цепи Маркова . [25] Классическая компартментальная модель в эпидемиологии — это модель SIR, которая может использоваться как простая модель для моделирования эпидемий. Также используются и другие типы компартментальных моделей.

Модель SIR

Диаграмма модели SIR с начальными значениями , а также показателями заражения и выздоровления С ( 0 ) = 997 , я ( 0 ) = 3 , Р ( 0 ) = 0 {\textstyle S(0)=997,I(0)=3,R(0)=0} β = 0,4 {\textstyle \бета =0,4} γ = 0,04 {\textstyle \гамма =0,04}
Анимация модели SIR с начальными значениями и скоростью выздоровления . Анимация показывает эффект снижения скорости заражения от до . Если нет доступных лекарств или вакцинации, снизить скорость заражения (часто называемую « сглаживанием кривой ») можно только соответствующими мерами, такими как социальное дистанцирование. С ( 0 ) = 997 , я ( 0 ) = 3 , Р ( 0 ) = 0 {\textstyle S(0)=997,I(0)=3,R(0)=0} γ = 0,04 {\textstyle \гамма =0,04} β = 0,5 {\textstyle \бета =0,5} β = 0,12 {\textstyle \бета =0,12}

В 1927 году WO Kermack и AG McKendrick создали модель, в которой они рассматривали фиксированную популяцию только с тремя отсеками: восприимчивый, ; инфицированный, ; и выздоровевший, . Отсеки, используемые для этой модели, состоят из трех классов: [26] С ( т ) {\displaystyle S(т)} я ( т ) {\displaystyle I(т)} Р ( т ) {\displaystyle R(т)}

  • С ( т ) {\displaystyle S(т)} , или восприимчивых к заболеванию представителей населения.
  • я ( т ) {\displaystyle I(т)} обозначает лиц из популяции, инфицированных данным заболеванием и способных передавать заболевание лицам, входящим в восприимчивую категорию.
  • Р ( т ) {\displaystyle R(т)} это отсек, используемый для лиц из популяции, которые были инфицированы, а затем выведены из болезни либо из-за иммунизации, либо из-за смерти. Те, кто относится к этой категории, не могут быть инфицированы снова или передать инфекцию другим.

Другие модели с отсеками

Существует множество модификаций модели SIR, в том числе те, которые включают в себя рождение и смерть, где после выздоровления иммунитет отсутствует (модель SIS), где иммунитет сохраняется только в течение короткого периода времени (SIRS), где существует латентный период болезни, когда человек не заразен ( SEIS и SEIR ), и где младенцы могут рождаться с иммунитетом (MSIR). [ необходима ссылка ]

Динамика инфекционных заболеваний

Математические модели должны интегрировать растущий объем данных , генерируемых по взаимодействиям хозяина и патогена . Многие теоретические исследования динамики популяции , структуры и эволюции инфекционных заболеваний растений и животных, включая людей, посвящены этой проблеме. [27]

Темы исследований включают:

Математика массовой вакцинации

Если доля населения, обладающего иммунитетом, превышает уровень коллективного иммунитета к заболеванию, то заболевание больше не может сохраняться в популяции, и его передача прекращается. [28] Таким образом, заболевание может быть устранено из популяции, если достаточное количество людей обладает иммунитетом либо благодаря вакцинации, либо благодаря выздоровлению от предшествующего воздействия заболевания. Например, искоренение оспы , с последним диким случаем в 1977 году, и сертификация искоренения местной передачи 2 из 3 типов дикого полиовируса (тип 2 в 2015 году, после последнего зарегистрированного случая в 1999 году, и тип 3 в 2019 году, после последнего зарегистрированного случая в 2012 году). [29]

Уровень коллективного иммунитета будет обозначаться q . Напомним, что для стабильного состояния: [ необходима цитата ]

Р 0 ⋅ С = 1. {\displaystyle R_{0}\cdot S=1.}

По очереди,

Р 0 = Н С = μ Н Э ⁡ ( Т Л ) μ Н Э ⁡ [ мин ( Т Л , Т С ) ] = Э ⁡ ( Т Л ) Э ⁡ [ мин ( Т Л , Т С ) ] , {\displaystyle R_{0}={\frac {N}{S}}={\frac {\mu N\operatorname {E} (T_{L})}{\mu N\operatorname {E} [\min(T_{L},T_{S})]}}={\frac {\operatorname {E} (T_{L})}{\operatorname {E} [\min(T_{L},T_{S})]}},}

что приблизительно составляет: [ необходима цитата ]

Э ⁡ ( Т Л ) Э ⁡ ( Т С ) = 1 + λ μ = β Н в . {\displaystyle {\frac {\operatorname {\operatorname {E} } (T_{L})}{\operatorname {\operatorname {E} } (T_{S})}}=1+{\frac {\lambda }{\mu }}={\frac {\beta N}{v}}.}
График зависимости порога коллективного иммунитета от базового числа воспроизводства при выбранных заболеваниях

S будет (1 −  q ), поскольку q — это доля населения, которая имеет иммунитет, а q  +  S должно быть равно единице (поскольку в этой упрощенной модели каждый либо восприимчив, либо имеет иммунитет). Тогда:

Р 0 ⋅ ( 1 − д ) = 1 , 1 − д = 1 Р 0 , д = 1 − 1 Р 0 . {\displaystyle {\begin{align}&R_{0}\cdot (1-q)=1,\\[6pt]&1-q={\frac {1}{R_{0}}},\\[6pt]&q=1-{\frac {1}{R_{0}}}.\end{align}}}

Помните, что это пороговый уровень. Вымирание от передачи произойдет только в том случае, если доля иммунных лиц превысит этот уровень из-за программы массовой вакцинации.

Мы только что рассчитали критический порог иммунизации (обозначаемый q c ). Это минимальная доля населения, которая должна быть иммунизирована при рождении (или близко к рождению), чтобы инфекция в популяции исчезла.

д с = 1 − 1 Р 0 . {\displaystyle q_{c}=1-{\frac {1}{R_{0}}}.}

Потому что доля окончательной численности популяции p , которая никогда не заражается, может быть определена как:

lim t → ∞ S ( t ) = e − ∫ 0 ∞ λ ( t ) d t = 1 − p . {\displaystyle \lim _{t\to \infty }S(t)=e^{-\int _{0}^{\infty }\lambda (t)\,dt}=1-p.}

Следовательно,

p = 1 − e − ∫ 0 ∞ β I ( t ) d t = 1 − e − R 0 p . {\displaystyle p=1-e^{-\int _{0}^{\infty }\beta I(t)\,dt}=1-e^{-R_{0}p}.}

Решая для , получаем: R 0 {\displaystyle R_{0}}

R 0 = − ln ⁡ ( 1 − p ) p . {\displaystyle R_{0}={\frac {-\ln(1-p)}{p}}.}

Когда массовая вакцинация не может превзойти коллективный иммунитет

Если используемая вакцина недостаточно эффективна или требуемый охват не может быть достигнут, программа может не превысить q c . Такая программа защитит вакцинированных людей от болезни, но может изменить динамику передачи. [ необходима цитата ]

Предположим, что часть населения q (где q < q c ) привита при рождении от инфекции с R 0  > 1. Программа вакцинации изменяет R 0 на R q , где

R q = R 0 ( 1 − q ) {\displaystyle R_{q}=R_{0}(1-q)}

Это изменение происходит просто потому, что в популяции теперь меньше восприимчивых людей, которые могут быть инфицированы. R q — это просто R 0 минус те, кто в обычных условиях был бы инфицирован, но не может быть инфицирован сейчас, поскольку они обладают иммунитетом.

Вследствие этого более низкого базового числа воспроизводства средний возраст инфицирования A также изменится на некоторое новое значение A q у тех, кто остался невакцинированным.

Вспомним соотношение, связывающее R 0 , A и L . Предполагая, что продолжительность жизни не изменилась, теперь: [ необходима цитата ]

R q = L A q , {\displaystyle R_{q}={\frac {L}{A_{q}}},}
A q = L R q = L R 0 ( 1 − q ) . {\displaystyle A_{q}={\frac {L}{R_{q}}}={\frac {L}{R_{0}(1-q)}}.}

Но R 0 = L / A, поэтому:

A q = L ( L / A ) ( 1 − q ) = A L L ( 1 − q ) = A 1 − q . {\displaystyle A_{q}={\frac {L}{(L/A)(1-q)}}={\frac {AL}{L(1-q)}}={\frac {A}{1-q}}.}

Таким образом, программа вакцинации может повысить средний возраст инфицирования, а невакцинированные лица будут испытывать меньшую силу инфицирования из-за присутствия вакцинированной группы. Для заболевания, которое приводит к большей клинической тяжести у пожилых людей, невакцинированная часть населения может испытать болезнь относительно позже в жизни, чем это произошло бы при отсутствии вакцины.

Когда массовая вакцинация превосходит коллективный иммунитет

Если программа вакцинации приводит к тому, что доля иммунных лиц в популяции превышает критический порог в течение значительного периода времени, передача инфекционного заболевания в этой популяции прекращается. Если ликвидация происходит везде в одно и то же время, то это может привести к искоренению . [ необходима цитата ]

Устранение
Прерывание эндемической передачи инфекционного заболевания, которое происходит, если каждый инфицированный человек заражает меньше, чем одного другого, достигается путем поддержания охвата вакцинацией, чтобы поддерживать долю иммунных людей выше критического порога иммунизации. [ необходима цитата ]
Искоренение
Уничтожение повсюду одновременно, в результате чего возбудитель инфекции вымирает (например, оспа и чума крупного рогатого скота ). [ необходима цитата ]

Надежность

Модели имеют преимущество в том, что они одновременно изучают несколько результатов, а не делают один прогноз. Модели показали высокую степень надежности в прошлых пандемиях, таких как SARS , SARS-CoV-2 , [30] свиной грипп , MERS и Эбола . [31]

Смотрите также

Ссылки

  1. ^ аб Дейли и Гани 1999, стр.  [ нужна страница ] .
  2. ^ Hethcote HW (2000). «Математика инфекционных заболеваний». SIAM Review . 42 (4): 599– 653. Bibcode : 2000SIAMR..42..599H. doi : 10.1137/S0036144500371907.
  3. ^ Блоуэр С., Бернулли Д. (2004). «Попытка нового анализа смертности, вызванной оспой, и преимуществ прививки для ее предотвращения». Обзоры по медицинской вирусологии . 14 (5): 275–88 . doi :10.1002/rmv.443. PMID  15334536.
  4. ^ Foppa IM (2017). "D. Bernoulli: A pioneer of epidemicologic modeling (1760)". Историческое введение в математическое моделирование инфекционных заболеваний . стр.  1– 20. doi :10.1016/B978-0-12-802260-3.00001-8. ISBN 978-0-12-802260-3.
  5. ^ Хамер 1929, стр.  [ нужна страница ] .
  6. ^ Росс 1910, стр.  [ нужна страница ] .
  7. ^ ab Brauer & Castillo-Chavez 2012, стр.  [ нужна страница ] .
  8. ^ Eisinger D, Thulke HH (апрель 2008 г.). «Формирование пространственной структуры способствует искоренению инфекционных заболеваний». Журнал прикладной экологии . 45 (2): 415– 423. Bibcode :2008JApEc..45..415E. doi :10.1111/j.1365-2664.2007.01439.x. PMC 2326892. PMID  18784795 . 
  9. ^ Адам Д. (апрель 2020 г.). «Специальный отчет: Моделирование, определяющее реакцию мира на COVID-19». Nature . 580 (7803): 316– 318. Bibcode :2020Natur.580..316A. doi : 10.1038/d41586-020-01003-6 . PMID  32242115.
  10. ^ Squazzoni F, Polhill JG, Edmonds B, Ahrweiler P, Antosz P, Scholz G, et al. (2020). «Вычислительные модели, имеющие значение во время глобальной вспышки пандемии: призыв к действию». Журнал искусственных обществ и социального моделирования . 23 (2). doi : 10.18564/jasss.4298 . hdl : 10037/19057 .
  11. ^ Шридхар Д., Маджумдер М.С. (апрель 2020 г.). «Моделирование пандемии». BMJ . 369 : m1567. doi : 10.1136/bmj.m1567 . PMID  32317328.
  12. ^ Maziarz M, Zach M (октябрь 2020 г.). «Моделирование на основе агентов для прогнозирования эпидемии SARS-CoV-2 и оценки вмешательства: методологическая оценка». Журнал оценки в клинической практике . 26 (5): 1352–1360 . doi :10.1111/jep.13459. PMC 7461315. PMID  32820573 . 
  13. ^ Huppert A, Katriel G (2013). «Математическое моделирование и прогнозирование в эпидемиологии инфекционных заболеваний». Клиническая микробиология и инфекция . 19 (11): 999–1005 . doi : 10.1111/1469-0691.12308 . PMID  24266045.
  14. ^ Тембин Х (3 ноября 2020 г.). «COVID-19: перспектива игры типа «усредненное поле», основанная на данных». Игры . 11 (4): 51. doi : 10.3390/g11040051 . hdl : 10419/257469 .
  15. ^ Nakamura GM, Monteiro AC, Cardoso GC, Martinez AS (20 января 2017 г.). "Эффективный метод комплексного вычисления распространения эпидемий на уровне агентов в сетях". Scientific Reports . 7 (1): 40885. arXiv : 1606.07825 . Bibcode :2017NatSR...740885N. doi :10.1038/srep40885. PMC 5247741 . PMID  28106086. 
  16. ^ Nakamura GM, Cardoso GC, Martinez AS (февраль 2020 г.). «Улучшенные уравнения восприимчивость–инфекционность–восприимчивость к эпидемиям на основе неопределенностей и автокорреляционных функций». Royal Society Open Science . 7 (2): 191504. Bibcode :2020RSOS....791504N. doi :10.1098/rsos.191504. PMC 7062106 . PMID  32257317. 
  17. ^ Dietz K (1967). «Эпидемии и слухи: обзор». Журнал Королевского статистического общества. Серия A (общая) . 130 (4): 505–528 . doi :10.2307/2982521. JSTOR  2982521.
  18. ^ Albi G, Bertaglia G, Boscheri W, Dimarco G, Pareschi L, Toscani G и др. (2022). «Кинетическое моделирование динамики эпидемий: социальные контакты, управление с неопределенными данными и многомасштабная пространственная динамика». Прогнозирование пандемий в глобально связанном мире, том 1. Моделирование и имитация в науке, технике и технологиях. стр.  43–108 . doi :10.1007/978-3-030-96562-4_3. ISBN 978-3-030-96561-7.
  19. ^ Майер Б.Ф., Брокманн Д. (2020). «Эффективное сдерживание объясняет субэкспоненциальный рост недавних подтвержденных случаев COVID-19 в Китае». Science . 368 (6492): 742– 746. Bibcode :2020Sci...368..742M. doi :10.1126/science.abb4557. PMC 7164388 . PMID  32269067. 
  20. ^ Барабаши 2016, с.  [ нужна страница ] .
  21. ^ Kenah E, Robins JM (сентябрь 2007 г.). «Второй взгляд на распространение эпидемий в сетях». Physical Review E. 76 ( 3 Pt 2): 036113. arXiv : q-bio/0610057 . Bibcode : 2007PhRvE..76c6113K. doi : 10.1103/PhysRevE.76.036113. PMC 2215389. PMID  17930312 . 
  22. ^ Пастор-Саторрас Р., Кастеллано С., Ван Мигем П., Веспиньяни А. (2015-08-31). «Эпидемические процессы в сложных сетях». Reviews of Modern Physics . 87 (3): 925–979 . arXiv : 1408.2701 . Bibcode :2015RvMP...87..925P. doi : 10.1103/RevModPhys.87.925 .
  23. ^ Rizi AK, Faqeeh A, Badie-Modiri A, Kivelä M (20 апреля 2022 г.). «Эпидемическое распространение и отслеживание цифровых контактов: эффекты гетерогенного смешивания и неудачи карантина». Physical Review E. 105 ( 4): 044313. arXiv : 2103.12634 . Bibcode : 2022PhRvE.105d4313R. doi : 10.1103/PhysRevE.105.044313 . PMID  35590624.
  24. ^ Миллер Э. (2003). «Глобальное бремя болезней». Книга о вакцинах . С.  37–50 . doi :10.1016/B978-012107258-2/50005-6. ISBN 978-0-12-107258-2.
  25. ^ Косма Шализи (15 ноября 2018 г.). «Данные в пространстве и времени; Лекция 21: Модели отсеков» (PDF) . Университет Карнеги — Меллона . Получено 19 сентября 2020 г. .
  26. ^ Kermack WO, McKendrick AG (1991). "Вклад в математическую теорию эпидемий--I. 1927". Bulletin of Mathematical Biology . 53 ( 1– 2): 33– 55. Bibcode :1927RSPSA.115..700K. doi : 10.1007/BF02464423 . JSTOR  94815. PMID  2059741.
  27. ^ Brauer F (2017). «Математическая эпидемиология: прошлое, настоящее и будущее». Моделирование инфекционных заболеваний . 2 (2): 113– 127. doi :10.1016/j.idm.2017.02.001. PMC 6001967. PMID  29928732 . 
  28. ^ Бриттон Т., Болл Ф., Трапман П. (2020). «Математическая модель раскрывает влияние гетерогенности популяции на коллективный иммунитет к SARS-CoV-2». Science . 369 (6505): 846– 849. Bibcode :2020Sci...369..846B. doi :10.1126/science.abc6810. PMC 7331793 . PMID  32576668. 
  29. ^ Поллард А. Дж., Бийкер Э. М. (2021). «Руководство по вакцинологии: от основных принципов к новым разработкам». Nature Reviews Immunology . 21 (2): 83– 100. doi :10.1038/s41577-020-00479-7. PMC 7754704. PMID 33353987  . 
  30. ^ Ренц А., Видерспик Л., Дрэгер А. (30 декабря 2020 г.). «FBA раскрывает гуанилаткиназу как потенциальную цель для противовирусной терапии против SARS-CoV-2». Биоинформатика . 36 (Приложение_2): i813 – i821 . doi : 10.1093/bioinformatics/btaa813. PMC 7773487. PMID  33381848.  
  31. ^ Costris-Vas C, Schwartz EJ, Smith? RJ (ноябрь 2020 г.). «Прогнозирование COVID-19 с использованием прошлых пандемий в качестве руководства: насколько надежными были математические модели тогда и насколько надежными они будут сейчас?». Mathematical Biosciences and Engineering . 17 (6): 7502– 7518. doi : 10.3934/mbe.2020383 (неактивен 1 ноября 2024 г.). PMID  33378907.{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)

Источники

  • Барабаси А.Л. (2016). Сетевая наука . Издательство Кембриджского университета. ISBN 978-1-107-07626-6.
  • Brauer F, Castillo-Chavez C (2012). Математические модели в популяционной биологии и эпидемиологии . Тексты по прикладной математике. Том 40. doi :10.1007/978-1-4614-1686-9. ISBN 978-1-4614-1685-2.
  • Daley DJ, Gani JM (1999). Моделирование эпидемий: Введение . Cambridge University Press. ISBN 978-0-521-01467-0.
  • Хамер WH (1929). Эпидемиология, старая и новая . Macmillan. hdl : 2027/mdp.39015006657475 . OCLC  609575950.
  • Росс Р. (1910). Профилактика малярии . Даттон. hdl : 2027/uc2.ark:/13960/t02z1ds0q . OCLC  610268760.

Дальнейшее чтение

  • Килинг М., Рохани П. Моделирование инфекционных заболеваний: у людей и животных . Принстон: Издательство Принстонского университета.
  • фон Чефалвай К. Вычислительное моделирование инфекционных заболеваний. Кембридж, Массачусетс: Elsevier/Academic Press . Получено 27.02.2023 .
  • Винницкий Э., Уайт Р. Г. Введение в моделирование инфекционных заболеваний . Получено 15.02.2016 .Вводная книга по моделированию инфекционных заболеваний и его применению.
  • Grassly NC, Fraser C (июнь 2008 г.). «Математические модели передачи инфекционных заболеваний». Nature Reviews. Microbiology . 6 (6): 477– 87. doi :10.1038/nrmicro1845. PMC  7097581. PMID  18533288 .
  • Boily MC, Mâsse B (июль–авг. 1997 г.). «Математические модели передачи заболеваний: ценный инструмент для изучения заболеваний, передающихся половым путем». Канадский журнал общественного здравоохранения . 88 (4): 255– 65. doi :10.1007/BF03404793. PMC  6990198. PMID  9336095 .
  • Математические структуры эпидемических систем . Конспект лекций по биоматематике. Том 97. 1993. doi :10.1007/978-3-540-70514-7. ISBN 978-3-540-56526-0.
Программное обеспечение
  • Model-Builder: интерактивное (на основе графического интерфейса) программное обеспечение для построения, моделирования и анализа моделей ОДУ.
  • Симулятор GLEaMviz: позволяет моделировать возникающие инфекционные заболевания, распространяющиеся по всему миру.
  • STEM: платформа с открытым исходным кодом для эпидемиологического моделирования, доступная через Eclipse Foundation.
  • R- пакет наблюдения: временное и пространственно-временное моделирование и мониторинг эпидемических явлений
Retrieved from "https://en.wikipedia.org/w/index.php?title=Mathematical_modelling_of_infectious_diseases&oldid=1267558085"