Кинетика ферментов

Кинетика ферментов — это изучение скоростей химических реакций , катализируемых ферментами . В кинетике ферментов измеряется скорость реакции и исследуются эффекты изменения условий реакции. Изучение кинетики фермента таким образом может раскрыть каталитический механизм этого фермента, его роль в метаболизме , как контролируется его активность и как лекарство или модификатор ( ингибитор или активатор ) могут повлиять на скорость.
Фермент (E) — это белковая молекула , которая служит биологическим катализатором для облегчения и ускорения химической реакции в организме. Она делает это посредством связывания другой молекулы, ее субстрата (S), на который фермент действует для образования желаемого продукта. Субстрат связывается с активным центром фермента, образуя комплекс фермент-субстрат ES, и преобразуется в комплекс фермент-продукт EP, а оттуда в продукт P, через переходное состояние ES*. Последовательность шагов известна как механизм :
- Э + С ⇄ ES ⇄ ES* ⇄ EP ⇄ E + P
В этом примере предполагается простейший случай реакции с одним субстратом и одним продуктом. Такие случаи существуют: например, мутаза , такая как фосфоглюкомутаза, катализирует перенос фосфатной группы из одного положения в другое, а изомераза — более общий термин для фермента, который катализирует любую односубстратную однопродуктовую реакцию, например, триозофосфатизомераза . Однако такие ферменты не очень распространены и значительно уступают по численности ферментам, катализирующим двухсубстратные двухпродуктовые реакции: к ним относятся, например, НАД-зависимые дегидрогеназы , такие как алкогольдегидрогеназа , которая катализирует окисление этанола НАД + . Реакции с тремя или четырьмя субстратами или продуктами встречаются реже, но они существуют. Нет необходимости, чтобы количество продуктов было равно количеству субстратов; например, глицеральдегид-3-фосфатдегидрогеназа имеет три субстрата и два продукта.
Когда ферменты связывают несколько субстратов, например, дигидрофолатредуктазу (показано справа), кинетика ферментов может также показать последовательность, в которой связываются эти субстраты, и последовательность, в которой высвобождаются продукты. Примером ферментов, которые связывают один субстрат и высвобождают несколько продуктов, являются протеазы , которые расщепляют один белковый субстрат на два полипептидных продукта. Другие соединяют два субстрата вместе, например, ДНК-полимераза, связывающая нуклеотид с ДНК . Хотя эти механизмы часто представляют собой сложную серию шагов, обычно существует один определяющий скорость шаг , который определяет общую кинетику. Этот определяющий скорость шаг может быть химической реакцией или конформационным изменением фермента или субстратов, например, тех, которые участвуют в высвобождении продукта(ов) из фермента.
Знание структуры фермента полезно для интерпретации кинетических данных. Например, структура может подсказать, как субстраты и продукты связываются во время катализа; какие изменения происходят во время реакции; и даже роль определенных аминокислотных остатков в механизме. Некоторые ферменты значительно изменяют форму во время механизма; в таких случаях полезно определить структуру фермента с и без связанных аналогов субстрата, которые не подвергаются ферментативной реакции.
Не все биологические катализаторы являются белковыми ферментами: катализаторы на основе РНК , такие как рибозимы и рибосомы, необходимы для многих клеточных функций, таких как сплайсинг и трансляция РНК . Главное различие между рибозимами и ферментами заключается в том, что катализаторы РНК состоят из нуклеотидов, тогда как ферменты состоят из аминокислот. Рибозимы также выполняют более ограниченный набор реакций, хотя механизмы их реакций и кинетику можно проанализировать и классифицировать теми же методами.
Общие принципы

Реакция, катализируемая ферментом, использует точно такие же реагенты и производит точно такие же продукты, как и некатализируемая реакция. Как и другие катализаторы , ферменты не изменяют положение равновесия между субстратами и продуктами. [1] Однако, в отличие от некатализируемых химических реакций, реакции, катализируемые ферментами, демонстрируют кинетику насыщения. Для заданной концентрации фермента и для относительно низких концентраций субстрата скорость реакции увеличивается линейно с концентрацией субстрата; молекулы фермента в значительной степени свободны катализировать реакцию, а увеличение концентрации субстрата означает увеличение скорости, с которой молекулы фермента и субстрата сталкиваются друг с другом. Однако при относительно высоких концентрациях субстрата скорость реакции асимптотически приближается к теоретическому максимуму; активные центры фермента почти все заняты субстратами, что приводит к насыщению, а скорость реакции определяется собственной скоростью оборота фермента. [2] Концентрация субстрата на полпути между этими двумя предельными случаями обозначается как K M . Таким образом, K M — это концентрация субстрата, при которой скорость реакции составляет половину максимальной скорости. [2]
Два важных свойства ферментативной кинетики — насколько легко фермент может быть насыщен субстратом и какова максимальная скорость, которую он может достичь. Знание этих свойств позволяет предположить, что фермент может делать в клетке, и может показать, как фермент будет реагировать на изменения в этих условиях.
Анализы ферментов

Анализы ферментов — это лабораторные процедуры, которые измеряют скорость ферментативных реакций. Поскольку ферменты не расходуются в реакциях, которые они катализируют, анализы ферментов обычно отслеживают изменения в концентрации субстратов или продуктов для измерения скорости реакции. Существует много методов измерения. Спектрофотометрические анализы наблюдают за изменением поглощения света между продуктами и реагентами; радиометрические анализы включают включение или высвобождение радиоактивности для измерения количества продукта, полученного с течением времени. Спектрофотометрические анализы наиболее удобны, поскольку они позволяют непрерывно измерять скорость реакции. Хотя радиометрические анализы требуют удаления и подсчета образцов (т. е. они являются прерывистыми анализами), они обычно чрезвычайно чувствительны и могут измерять очень низкие уровни активности ферментов. [3] Аналогичный подход заключается в использовании масс-спектрометрии для мониторинга включения или высвобождения стабильных изотопов по мере того, как субстрат превращается в продукт. Иногда анализ терпит неудачу, и для восстановления неудавшегося анализа необходимы подходы.
Наиболее чувствительные ферментные анализы используют лазеры , сфокусированные через микроскоп, для наблюдения за изменениями в отдельных молекулах фермента, когда они катализируют свои реакции. Эти измерения используют либо изменения флуоресценции кофакторов во время механизма реакции фермента, либо флуоресцентные красители, добавленные на определенные участки белка, чтобы сообщать о движениях, которые происходят во время катализа. [4] Эти исследования дают новый взгляд на кинетику и динамику отдельных ферментов, в отличие от традиционной ферментной кинетики, которая наблюдает за средним поведением популяций миллионов молекул фермента. [5] [6]
Пример кривой прогресса для ферментного анализа показан выше. Фермент производит продукт с начальной скоростью, которая приблизительно линейна в течение короткого периода после начала реакции. По мере протекания реакции и потребления субстрата скорость непрерывно замедляется (до тех пор, пока субстрат не достигнет уровня насыщения). Для измерения начальной (и максимальной) скорости ферментные анализы обычно проводятся, когда реакция продвинулась всего на несколько процентов к полному завершению. Длительность периода начальной скорости зависит от условий анализа и может варьироваться от миллисекунд до часов. Однако оборудование для быстрого смешивания жидкостей позволяет проводить быстрые кинетические измерения с начальной скоростью менее одной секунды. [7] Эти очень быстрые анализы необходимы для измерения кинетики до стационарного состояния, которая обсуждается ниже.
Большинство исследований кинетики ферментов сосредоточены на этой начальной, приблизительно линейной части ферментативных реакций. Однако также возможно измерить полную кривую реакции и подогнать эти данные к нелинейному уравнению скорости . Этот способ измерения ферментативных реакций называется анализом кривой прогресса. [8] Этот подход полезен как альтернатива быстрой кинетике, когда начальная скорость слишком велика для точного измерения.
Стандарты для отчетности по данным энзимологии Руководящие принципы предоставляют минимальную информацию, необходимую для всестороннего отчета по кинетическим и равновесным данным исследований активности ферментов, включая соответствующие экспериментальные условия. Руководящие принципы были разработаны для отчетности по функциональным данным ферментов со строгостью и надежностью.
Реакции с одним субстратом
Ферменты с механизмами с одним субстратом включают изомеразы , такие как триозофосфатизомераза или бисфосфоглицератмутаза , внутримолекулярные лиазы, такие как аденилатциклаза и рибозим «молоток» , РНК-лиаза. [9] Однако некоторые ферменты, которые имеют только один субстрат, не попадают в эту категорию механизмов. Каталаза является примером этого, поскольку фермент реагирует с первой молекулой субстрата перекиси водорода , окисляется и затем восстанавливается второй молекулой субстрата. Хотя задействован один субстрат, существование модифицированного промежуточного фермента означает, что механизм каталазы на самом деле является механизмом пинг-понга, типом механизма, который обсуждается в разделе « Реакции с несколькими субстратами» ниже.
Кинетика Михаэлиса–Ментена
Поскольку реакции, катализируемые ферментами, являются насыщаемыми, их скорость катализа не показывает линейного ответа на увеличение субстрата. Если начальная скорость реакции измеряется в диапазоне концентраций субстрата (обозначается как [S]), начальная скорость реакции ( ) увеличивается с увеличением [S], как показано справа. Однако по мере того, как [S] становится выше, фермент насыщается субстратом, и начальная скорость достигает V max , максимальной скорости фермента.
Справа показана кинетическая модель Михаэлиса-Ментен реакции с одним субстратом. Существует начальная бимолекулярная реакция между ферментом E и субстратом S с образованием комплекса фермент-субстрат ES. Скорость ферментативной реакции увеличивается с увеличением концентрации субстрата до определенного уровня, называемого V max ; при V max увеличение концентрации субстрата не вызывает увеличения скорости реакции, поскольку больше нет фермента (E), доступного для реакции с субстратом (S). Здесь скорость реакции становится зависимой от комплекса ES, и реакция становится мономолекулярной реакцией с нулевым порядком. Хотя ферментативный механизм для мономолекулярной реакции может быть довольно сложным, обычно существует один определяющий скорость ферментативный этап, который позволяет моделировать эту реакцию как один каталитический этап с кажущейся мономолекулярной константой скорости k cat . Если путь реакции протекает через один или несколько промежуточных продуктов, k cat будет функцией нескольких элементарных констант скорости, тогда как в простейшем случае одной элементарной реакции (например, без промежуточных продуктов) она будет идентична элементарной мономолекулярной константе скорости k 2 . Кажущаяся мономолекулярная константа скорости k cat также называется числом оборотов и обозначает максимальное число ферментативных реакций, катализируемых в секунду.
Уравнение Михаэлиса–Ментен [10] описывает, как (начальная) скорость реакции v 0 зависит от положения равновесия связывания субстрата и константы скорости k 2 .
- (Уравнение Михаэлиса–Ментена)
с константами
Это уравнение Михаэлиса-Ментен является основой для большинства односубстратных ферментативных кинетик. В основе этого уравнения лежат два важных предположения (помимо общего предположения о том, что механизм не включает в себя ингибирование промежуточных или продуктов, и нет аллостеричности или кооперативности ). Первое предположение — это так называемое предположение о квазистационарном состоянии (или гипотеза псевдостационарного состояния), а именно, что концентрация связанного с субстратом фермента (и, следовательно, также несвязанного фермента) изменяется гораздо медленнее, чем концентрация продукта и субстрата, и, таким образом, изменение комплекса с течением времени можно приравнять к нулю . Второе предположение заключается в том, что общая концентрация фермента не изменяется с течением времени, таким образом .
Константа Михаэлиса K M экспериментально определяется как концентрация, при которой скорость ферментативной реакции составляет половину V max , что можно проверить, подставив [S] = K M в уравнение Михаэлиса–Ментен, а также можно увидеть графически. Если скоростьопределяющий ферментативный этап медленнее по сравнению с диссоциацией субстрата ( ), константа Михаэлиса K M примерно равна константе диссоциации K D комплекса ES.
Если мало по сравнению с то термин и также очень мало ES комплекса образуется, таким образом . Поэтому скорость образования продукта равна
Таким образом, скорость образования продукта зависит от концентрации фермента, а также от концентрации субстрата, уравнение напоминает бимолекулярную реакцию с соответствующей константой скорости псевдовторого порядка . Эта константа является мерой каталитической эффективности . Наиболее эффективные ферменты достигают a в диапазоне 10 8 – 10 10 М −1 с −1 . Эти ферменты настолько эффективны, что эффективно катализируют реакцию каждый раз, когда сталкиваются с молекулой субстрата, и, таким образом, достигают верхнего теоретического предела эффективности ( предела диффузии ); и иногда их называют кинетически совершенными ферментами . [11] Но большинство ферментов далеки от совершенства: средние значения и составляют около и соответственно. [12]
Прямое использование уравнения Михаэлиса–Ментен для анализа кинетики течения времени
Наблюдаемые скорости, предсказанные уравнением Михаэлиса–Ментен, могут быть использованы для прямого моделирования исчезновения субстрата во времени и производства продукта посредством включения уравнения Михаэлиса–Ментен в уравнение для химической кинетики первого порядка. Однако этого можно достичь только в том случае, если осознать проблему, связанную с использованием числа Эйлера при описании химической кинетики первого порядка. т.е. e − k является разделенной константой, которая вносит систематическую ошибку в расчеты и может быть переписана как одна константа, которая представляет оставшийся субстрат после каждого периода времени. [13]
В 1983 году Стюарт Бил (а также независимо Сантьяго Шнелл и Клаудио Мендоса в 1997 году) вывели решение в замкнутой форме для анализа кинетики хода времени механизма Михаэлиса-Ментен. [14] [15] Решение, известное как уравнение Шнелла-Мендосы, имеет вид:
где W[ ] — функция Ламберта-W . [16] [17] и где F(t) —
Это уравнение охватывается приведенным ниже уравнением, полученным Бербераном-Сантосом [18], которое также справедливо, когда начальная концентрация субстрата близка к концентрации фермента:
где W[ ] снова является функцией Ламберта-W .
Линейные графики уравнения Михаэлиса–Ментен
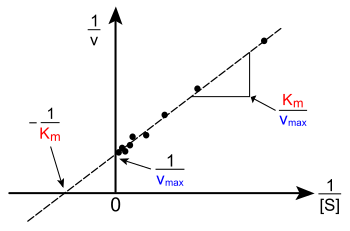
График зависимости v от [S] выше не является линейным; хотя изначально линейный при низком [S], он изгибается, чтобы насытиться при высоком [S]. До современной эры нелинейной подгонки кривых на компьютерах эта нелинейность могла затруднить точную оценку K M и V max . Поэтому несколько исследователей разработали линеаризации уравнения Михаэлиса–Ментен, такие как график Лайнуивера–Берка , диаграмма Иди–Хофсти и график Хейнса–Вульфа . Все эти линейные представления могут быть полезны для визуализации данных, но ни одно из них не следует использовать для определения кинетических параметров, поскольку компьютерное программное обеспечение легко доступно, что позволяет проводить более точное определение методами нелинейной регрессии . [19]
График Лайнуивера –Берка или двойной обратный график — это распространенный способ иллюстрации кинетических данных. Он получается путем взятия обратной величины обеих сторон уравнения Михаэлиса–Ментен. Как показано справа, это линейная форма уравнения Михаэлиса–Ментен, которая создает прямую линию с уравнением y = m x + c с пересечением по оси y, эквивалентным 1/ V max , и пересечением по оси x графика, представляющим −1/ K M .
Естественно, никакие экспериментальные значения не могут быть получены при отрицательном 1/[S]; нижнее предельное значение 1/[S] = 0 ( пересечение по оси y ) соответствует бесконечной концентрации субстрата, где 1/v=1/V max , как показано справа; таким образом, пересечение по оси x является экстраполяцией экспериментальных данных, полученных при положительных концентрациях. В более общем смысле, график Лайнуивера–Берка искажает важность измерений, полученных при низких концентрациях субстрата, и, таким образом, может давать неточные оценки V max и K M . [20] Более точным методом линейного построения графика является график Иди–Хофсти . В этом случае v отображается в зависимости от v /[S]. В третьем общем линейном представлении, графике Хейнса–Вульфа , [S]/ v отображается в зависимости от [S]. В общем, нормализация данных может помочь уменьшить объем экспериментальной работы и повысить надежность выходных данных, и подходит как для графического, так и для численного анализа. [21]
Практическое значение кинетических констант
Изучение кинетики ферментов важно по двум основным причинам. Во-первых, оно помогает объяснить, как работают ферменты, а во-вторых, оно помогает предсказать, как ферменты ведут себя в живых организмах. Определенные выше кинетические константы, K M и V max , имеют решающее значение для попыток понять, как ферменты работают вместе, чтобы контролировать метаболизм .
Создание таких прогнозов не является тривиальной задачей даже для простых систем. Например, оксалоацетат образуется малатдегидрогеназой в митохондриях . Затем оксалоацетат может потребляться цитратсинтазой , фосфоенолпируваткарбоксикиназой или аспартатаминотрансферазой , поступая в цикл лимонной кислоты , глюконеогенез или биосинтез аспарагиновой кислоты соответственно. Возможность предсказать, сколько оксалоацетата пойдет в какой путь, требует знания концентрации оксалоацетата, а также концентрации и кинетики каждого из этих ферментов. Эта цель прогнозирования поведения метаболических путей достигает своего наиболее сложного выражения в синтезе огромных объемов кинетических и генных данных в математические модели целых организмов. В качестве альтернативы, одним из полезных упрощений проблемы метаболического моделирования является игнорирование базовой ферментативной кинетики и опора только на информацию о стехиометрии реакционной сети, метод, называемый анализом баланса потоков . [22] [23]
Кинетика Михаэлиса–Ментена с промежуточным
Можно также рассмотреть менее простой случай
где существует комплекс с ферментом и промежуточным продуктом, а промежуточный продукт преобразуется в продукт на втором этапе. В этом случае мы имеем очень похожее уравнение [24]
но константы разные
Мы видим, что для предельного случая , таким образом, когда последний шаг из намного быстрее предыдущего шага, мы снова получаем исходное уравнение. Математически мы имеем тогда и .
Мультисубстратные реакции
Реакции с несколькими субстратами следуют сложным уравнениям скорости, которые описывают, как субстраты связываются и в какой последовательности. Анализ этих реакций намного проще, если концентрация субстрата A остается постоянной, а субстрат B варьируется. В этих условиях фермент ведет себя так же, как фермент с одним субстратом, и график v по [S] дает кажущиеся константы K M и V max для субстрата B. Если набор этих измерений выполняется при различных фиксированных концентрациях A, эти данные можно использовать для выяснения механизма реакции. Для фермента, который берет два субстрата A и B и превращает их в два продукта P и Q, существует два типа механизма: тройной комплекс и пинг-понг.
Тройно-комплексные механизмы

В этих ферментах оба субстрата связываются с ферментом одновременно, образуя тройной комплекс EAB. Порядок связывания может быть случайным (в случайном механизме) или субстраты должны связываться в определенной последовательности (в упорядоченном механизме). Когда набор кривых v по [S] (фиксированный A, изменяющийся B) от фермента с тройным комплексным механизмом отображается на графике Лайнуивера–Берка , набор полученных линий будет пересекаться.
Ферменты с тройным сложным механизмом включают глутатион- S -трансферазу , [25] дигидрофолатредуктазу [26] и ДНК-полимеразу . [27] По следующим ссылкам показаны короткие анимации тройного сложного механизма ферментов дигидрофолатредуктазы [β] и ДНК-полимеразы [γ] .
Механизмы для пинг-понга
Как показано справа, ферменты с механизмом пинг-понга могут существовать в двух состояниях: E и химически модифицированной форме фермента E*; этот модифицированный фермент известен как промежуточное вещество . В таких механизмах субстрат A связывается, изменяет фермент на E*, например, перенося химическую группу в активный центр, а затем высвобождается. Только после высвобождения первого субстрата субстрат B может связываться и реагировать с модифицированным ферментом, восстанавливая немодифицированную форму E. Когда набор кривых v по [S] (фиксированное A, изменяющееся B) от фермента с механизмом пинг-понга отображается на графике Лайнуивера–Берка, будет получен набор параллельных линий. Это называется вторичным графиком .
Ферменты с механизмами пинг-понга включают некоторые оксидоредуктазы , такие как тиоредоксинпероксидаза , [28] трансферазы, такие как ацилнейраминцитидилилтрансфераза [29] и сериновые протеазы, такие как трипсин и химотрипсин . [30] Сериновые протеазы являются очень распространенным и разнообразным семейством ферментов, включая пищеварительные ферменты (трипсин, химотрипсин и эластаза), несколько ферментов каскада свертывания крови и многие другие. В этих сериновых протеазах промежуточный продукт E* представляет собой ацил-ферментный вид, образованный атакой остатка серина активного центра на пептидную связь в белковом субстрате. Короткая анимация, показывающая механизм химотрипсина, приведена здесь. [δ]
Обратимый катализ и уравнение Холдейна
Внешние факторы могут ограничивать способность фермента катализировать реакцию в обоих направлениях (тогда как сама природа катализатора означает, что он не может катализировать только одно направление, согласно принципу микроскопической обратимости ). Рассмотрим случай фермента, который катализирует реакцию в обоих направлениях:
Стационарная начальная скорость реакции равна
является положительным, если реакция протекает в прямом направлении ( ), и отрицательным в противном случае.
Равновесие требует, чтобы , что происходит, когда . Это показывает, что термодинамика навязывает соотношение между значениями 4 констант скорости.
Значения максимальных скоростей вперед и назад, полученные для , , и , , соответственно, равны и , соответственно. Их отношение не равно константе равновесия, что подразумевает, что термодинамика не ограничивает отношение максимальных скоростей. Это объясняет, что ферменты могут быть гораздо «лучшими катализаторами» ( в терминах максимальных скоростей ) в одном конкретном направлении реакции. [31]
Можно также вывести две константы Михаэлиса и . Уравнение Холдейна — это соотношение .
Таким образом, термодинамика ограничивает соотношение между прямыми и обратными значениями, а не соотношение значений.
Кинетика, отличная от Михаэлиса-Ментена

Многие различные ферментные системы следуют поведению, отличному от поведения Михаэлиса-Ментен. Несколько избранных примеров включают кинетику самокаталитических ферментов, кооперативных и аллостерических ферментов, межфазных и внутриклеточных ферментов, процессивных ферментов и т. д. Некоторые ферменты производят сигмоидный график v на [S], который часто указывает на кооперативное связывание субстрата с активным сайтом. Это означает, что связывание одной молекулы субстрата влияет на связывание последующих молекул субстрата. Такое поведение наиболее распространено в мультимерных ферментах с несколькими взаимодействующими активными сайтами. [32] Здесь механизм кооперации аналогичен механизму гемоглобина , при этом связывание субстрата с одним активным сайтом изменяет сродство других активных сайтов к молекулам субстрата. Положительная кооперативность возникает, когда связывание первой молекулы субстрата увеличивает сродство других активных сайтов к субстрату. Отрицательная кооперативность возникает, когда связывание первого субстрата уменьшает сродство фермента к другим молекулам субстрата.
Аллостерические ферменты включают тирозил-тРНК-синтетазу млекопитающих, которая проявляет отрицательную кооперативность, [33] и бактериальную аспартаттранскарбамоилазу [34] и фосфофруктокиназу [35] , которые проявляют положительную кооперативность.
Кооперативность на удивление распространена и может помочь регулировать реакции ферментов на изменения концентраций их субстратов. Положительная кооперативность делает ферменты гораздо более чувствительными к [S], и их активность может демонстрировать большие изменения в узком диапазоне концентраций субстрата. Наоборот, отрицательная кооперативность делает ферменты нечувствительными к небольшим изменениям [S].
Уравнение Хилла [36] часто используется для количественного описания степени кооперативности в не-Михаэлис-Ментен кинетике. Выведенный коэффициент Хилла n измеряет, насколько сильно связывание субстрата с одним активным сайтом влияет на связывание субстрата с другими активными сайтами. Коэффициент Хилла <1 указывает на отрицательную кооперативность, а коэффициент >1 указывает на положительную кооперативность .
Кинетика до стационарного состояния

В первый момент после смешивания фермента с субстратом не образуется никакого продукта и не существует никаких промежуточных продуктов . Изучение следующих нескольких миллисекунд реакции называется предстационарной кинетикой. Таким образом, предстационарная кинетика связана с образованием и потреблением промежуточных продуктов фермент-субстрат (таких как ES или E*) до тех пор, пока не будут достигнуты их стационарные концентрации .
Этот подход был впервые применен к реакции гидролиза, катализируемой химотрипсином . [37] Часто обнаружение промежуточного продукта является жизненно важным доказательством в исследованиях того, какому механизму следует фермент. Например, в механизмах пинг-понга, которые показаны выше, быстрые кинетические измерения могут следить за высвобождением продукта P и измерять образование модифицированного промежуточного продукта фермента E*. [38] В случае химотрипсина этот промежуточный продукт образуется в результате атаки на субстрат нуклеофильным серином в активном центре и образования промежуточного продукта ацил-фермента.
На рисунке справа фермент быстро производит E* в первые несколько секунд реакции. Затем скорость замедляется по мере достижения устойчивого состояния. Эта быстрая фаза всплеска реакции измеряет один оборот фермента. Следовательно, количество продукта, высвобождаемого в этом всплеске, показанное как отсекаемый элемент на оси Y графика, также дает количество функционального фермента, который присутствует в анализе. [39]
Химический механизм
Важной целью измерения ферментативной кинетики является определение химического механизма ферментативной реакции, т. е. последовательности химических шагов, которые преобразуют субстрат в продукт. Кинетические подходы, обсуждавшиеся выше, покажут, с какой скоростью образуются и взаимопревращаются промежуточные продукты , но они не могут точно определить, что это за промежуточные продукты.
Кинетические измерения, проведенные в различных условиях раствора или на слегка модифицированных ферментах или субстратах, часто проливают свет на этот химический механизм, поскольку они выявляют этап, определяющий скорость, или промежуточные продукты в реакции. Например, разрыв ковалентной связи с атомом водорода является обычным этапом, определяющим скорость. Какой из возможных переносов водорода является определяющим скорость, можно показать, измерив кинетические эффекты замены каждого водорода дейтерием , его стабильным изотопом . Скорость изменится, когда будет заменен критический водород, из-за первичного кинетического изотопного эффекта , который возникает, поскольку связи с дейтерием труднее разорвать, чем связи с водородом. [40] Также возможно измерить подобные эффекты с другими изотопными заменами, такими как 13 C/ 12 C и 18 O/ 16 O, но эти эффекты более тонкие. [41]
Изотопы также могут быть использованы для выявления судьбы различных частей молекул субстрата в конечных продуктах. Например, иногда трудно определить происхождение атома кислорода в конечном продукте; так как он мог произойти из воды или из части субстрата. Это может быть определено путем систематической замены стабильного изотопа кислорода 18 O в различные молекулы, которые участвуют в реакции, и проверки изотопа в продукте. [42] Химический механизм также может быть выяснен путем изучения кинетики и изотопных эффектов при различных условиях pH, [43] путем изменения ионов металлов или других связанных кофакторов , [44] путем направленного мутагенеза консервативных аминокислотных остатков или путем изучения поведения фермента в присутствии аналогов субстрата(ов). [45]
Ингибирование и активация ферментов

Ингибиторы ферментов — это молекулы, которые снижают или отменяют активность ферментов, тогда как активаторы ферментов — это молекулы, которые увеличивают каталитическую скорость ферментов. Эти взаимодействия могут быть как обратимыми (т. е. удаление ингибитора восстанавливает активность фермента), так и необратимыми (т. е. ингибитор навсегда инактивирует фермент).
Обратимые ингибиторы
Традиционно обратимые ингибиторы ферментов классифицируются как конкурентные , неконкурентные или неконкурентные в соответствии с их влиянием на K M и V max . Эти различные эффекты являются результатом связывания ингибитора с ферментом E, с комплексом фермент-субстрат ES или с обоими, соответственно. Разделение этих классов возникает из-за проблемы в их выводе и приводит к необходимости использовать две разные константы связывания для одного события связывания. Связывание ингибитора и его влияние на ферментативную активность — это две совершенно разные вещи, еще одна проблема, которую традиционные уравнения не признают. При неконкурентном ингибировании связывание ингибитора приводит к 100% ингибированию только фермента и не учитывает возможность чего-либо между ними. [46] При неконкурентном ингибировании ингибитор будет связываться с ферментом в его аллостерическом сайте; следовательно, сродство связывания или обратное K M субстрата с ферментом останется прежним. С другой стороны, V max уменьшится по сравнению с неингибированным ферментом. На графике Лайнуивера-Берка наличие неконкурентного ингибитора иллюстрируется изменением y-отрезка, определяемого как 1/V max . X-отрезок, определяемый как −1/ K M , останется прежним. При конкурентном ингибировании ингибитор будет связываться с ферментом в активном центре, конкурируя с субстратом. В результате K M увеличится, а V max останется прежним. [47] Обычная форма ингибирующего термина также скрывает связь между связыванием ингибитора с ферментом и его связью с любым другим термином связывания, будь то уравнение Михаэлиса-Ментен или кривая доза-ответ, связанная со связыванием лиганда с рецептором. Чтобы продемонстрировать эту связь, можно сделать следующую перегруппировку:
Добавляем ноль к основанию ([I]-[I])
Деление на [I]+K i
Эта запись показывает, что подобно уравнению Михаэлиса-Ментен, где скорость реакции зависит от процента популяции фермента, взаимодействующей с субстратом, эффект ингибитора является результатом процента популяции фермента, взаимодействующей с ингибитором. Единственная проблема с этим уравнением в его нынешнем виде заключается в том, что оно предполагает абсолютное ингибирование фермента при связывании ингибитора, когда на самом деле может быть широкий диапазон эффектов от 100% ингибирования оборота субстрата до всего лишь >0%. Чтобы учесть это, уравнение можно легко модифицировать, чтобы учесть различные степени ингибирования, включив член delta V max .
или
Этот термин затем может определять остаточную ферментативную активность, присутствующую, когда ингибитор взаимодействует с отдельными ферментами в популяции. Однако включение этого термина имеет дополнительную ценность, позволяя возможность активации, если вторичный термин V max оказывается выше начального термина. Чтобы учесть также возможность активации, обозначение затем можно переписать, заменив ингибитор "I" на модификатор, обозначенный здесь как "X".
Хотя эта терминология приводит к упрощенному способу рассмотрения кинетических эффектов, связанных с максимальной скоростью уравнения Михаэлиса-Ментен, она подчеркивает потенциальные проблемы с термином, используемым для описания эффектов, связанных с K M . K M , относящийся к сродству фермента к субстрату, в большинстве случаев должен относиться к потенциальным изменениям в сайте связывания фермента, которые будут напрямую результатом взаимодействий ингибиторов фермента. Таким образом, термин, аналогичный предложенному выше для модуляции V max , должен быть уместен в большинстве ситуаций: [48]
Необратимые ингибиторы
Ингибиторы ферментов также могут необратимо инактивировать ферменты, обычно путем ковалентной модификации остатков активного центра. Эти реакции, которые можно назвать субстратами самоубийства, следуют экспоненциальным функциям распада и обычно являются насыщаемыми. Ниже насыщения они следуют кинетике первого порядка по отношению к ингибитору. Необратимое ингибирование можно разделить на два различных типа. Аффинная маркировка — это тип необратимого ингибирования, при котором функциональная группа, которая является высокореактивной, модифицирует каталитически важный остаток на интересующем белке, чтобы вызвать ингибирование. С другой стороны, ингибирование на основе механизма включает связывание ингибитора с последующими опосредованными ферментом изменениями, которые превращают последний в реактивную группу, которая необратимо модифицирует фермент.
Философский дискурс об обратимости и необратимости торможения
Обсудив обратимое и необратимое ингибирование в двух предыдущих заголовках, следует отметить, что концепция обратимости (или необратимости) является чисто теоретической конструкцией, зависящей исключительно от временных рамок анализа, т. е. обратимый анализ, включающий ассоциацию и диссоциацию молекулы ингибитора в минутных временных масштабах, будет казаться необратимым, если анализ оценивает результат в секундах, и наоборот. Существует континуум поведения ингибиторов, охватывающий обратимость и необратимость в заданных непроизвольных временных рамках анализа. Существуют ингибиторы, которые демонстрируют медленное начало поведения, и большинство из этих ингибиторов, неизменно, также демонстрируют прочное связывание с интересующей белковой мишенью.
Механизмы катализа

Предпочтительная модель взаимодействия фермента и субстрата — модель индуцированного соответствия. [49] Эта модель предполагает, что начальное взаимодействие между ферментом и субстратом относительно слабое, но что эти слабые взаимодействия быстро вызывают конформационные изменения в ферменте, которые усиливают связывание. Эти конформационные изменения также приближают каталитические остатки в активном центре к химическим связям в субстрате, которые будут изменены в реакции. [50] Конформационные изменения можно измерить с помощью кругового дихроизма или двойной поляризационной интерферометрии . После связывания один или несколько механизмов катализа снижают энергию переходного состояния реакции , предоставляя альтернативный химический путь для реакции. Механизмы катализа включают катализ за счет деформации связи; за счет близости и ориентации; за счет доноров или акцепторов протонов активного центра; ковалентный катализ и квантовое туннелирование . [38] [51]
Кинетика ферментов не может доказать, какие режимы катализа используются ферментом. Однако некоторые кинетические данные могут указывать на возможности для изучения другими методами. Например, механизм пинг-понга с кинетикой фазы взрыва до стационарного состояния предполагает, что ковалентный катализ может быть важен в механизме этого фермента. Альтернативно, наблюдение сильного влияния pH на V max , но не на K M может указывать на то, что остаток в активном центре должен находиться в определенном состоянии ионизации для осуществления катализа.
История
В 1902 году Виктор Анри предложил количественную теорию кинетики ферментов, [52] но в то время экспериментальное значение концентрации ионов водорода еще не было признано. После того, как Петер Лауриц Сёренсен определил логарифмическую шкалу pH и ввел концепцию буферизации в 1909 году [53], немецкий химик Леонор Михаэлис и доктор Мод Леонора Ментен (в то время научный сотрудник в лаборатории Михаэлиса) повторили эксперименты Анри и подтвердили его уравнение, которое теперь обычно называют кинетикой Михаэлиса-Ментена (иногда также кинетикой Анри-Михаэлиса-Ментена ). [54] Их работа была далее развита GE Briggs и JBS Haldane , которые вывели кинетические уравнения, которые до сих пор широко считаются отправной точкой в моделировании ферментативной активности. [55]
Основным вкладом подхода Анри-Михаэлиса-Ментена было представление ферментативных реакций в два этапа. На первом этапе субстрат обратимо связывается с ферментом, образуя комплекс фермент-субстрат. Иногда его называют комплексом Михаэлиса. Затем фермент катализирует химический этап реакции и высвобождает продукт. Кинетика многих ферментов адекватно описывается простой моделью Михаэлиса-Ментена, но все ферменты имеют внутренние движения , которые не учитываются в модели и могут вносить значительный вклад в общую кинетику реакции. Это можно смоделировать, введя несколько путей Михаэлиса-Ментена, которые связаны с флуктуирующими скоростями, [56] [57] [58], что является математическим расширением базового механизма Михаэлиса-Ментена. [59]
Программное обеспечение
ENZO (Enzyme Kinetics) — это графический интерфейсный инструмент для построения кинетических моделей реакций, катализируемых ферментами. ENZO автоматически генерирует соответствующие дифференциальные уравнения из заданной схемы ферментативной реакции. Эти дифференциальные уравнения обрабатываются численным решателем и алгоритмом регрессии, который подгоняет коэффициенты дифференциальных уравнений к экспериментально наблюдаемым кривым течения времени. ENZO позволяет быстро оценивать конкурирующие схемы реакций и может использоваться для рутинных тестов в кинетике ферментов. [60]
Смотрите также
Сноски
- α. ^ Ссылка: Интерактивный учебник по кинетике Михаэлиса–Ментен (требуется Java)
- β. ^ Ссылка: механизм дигидрофолатредуктазы (Gif)
- γ. ^ Ссылка: механизм ДНК-полимеразы (Gif)
- δ. ^ Ссылка: Механизм химотрипсина (требуется Flash)
Ссылки
- ^ Райтон М.С., Эббинг Д.Д. (1993). Общая химия (4-е изд.). Бостон: Houghton Mifflin. ISBN 978-0-395-63696-1.
- ^ ab Fromm HJ, Hargrove MS (2012) Кинетика ферментов. В: Основы биохимии. Springer, Берлин, Гейдельберг
- ^ Дэнсон М., Эйзенталь Р. (2002). Ферментные анализы: практический подход . Оксфорд [Оксфордшир]: Oxford University Press. ISBN 978-0-19-963820-8.
- ^ Xie XS, Lu HP (июнь 1999). «Одиночная молекулярная энзимология». Журнал биологической химии . 274 (23): 15967–15970. doi : 10.1074/jbc.274.23.15967 . PMID 10347141.
- ^ Lu HP (июнь 2004 г.). «Исследования динамики конформационных изменений в ферментативных реакциях с помощью спектроскопии отдельных молекул». Current Pharmaceutical Biotechnology . 5 (3): 261–269. doi :10.2174/1389201043376887. PMID 15180547.
- ^ Schnell JR, Dyson HJ , Wright PE (2004). «Структура, динамика и каталитическая функция дигидрофолатредуктазы». Annual Review of Biophysics and Biomolecular Structure . 33 : 119–140. doi :10.1146/annurev.biophys.33.110502.133613. PMID 15139807.
- ^ Gibson QH (1969). "[6] Быстрое смешивание: Остановленный поток". Быстрое смешивание: Остановленный поток . Методы в энзимологии. Том 16. С. 187–228. doi :10.1016/S0076-6879(69)16009-7. ISBN 978-0-12-181873-9.
- ^ Duggleby RG (1995). "[3] Анализ кривых прогресса фермента с помощью нелинейной регрессии". Анализ кривых прогресса фермента с помощью нелинейной регрессии . Методы в энзимологии. Т. 249. С. 61–90. doi :10.1016/0076-6879(95)49031-0. ISBN 978-0-12-182150-0. PMID 7791628.
- ^ Murray JB, Dunham CM, Scott WG (январь 2002 г.). «Зависимое от pH конформационное изменение, а не химический шаг, по-видимому, является ограничивающим скорость в реакции расщепления рибозима молоткообразной головкой». Журнал молекулярной биологии . 315 (2): 121–130. doi :10.1006/jmbi.2001.5145. PMID 11779233. S2CID 18102624.
- ^ Михаэлис Л. и Ментен М.Л. Кинетика дер Invertinwirkung Biochem. З. 1913 г.; 49:333–369 английский перевод, по состоянию на 6 апреля 2007 г.
- ^ Stroppolo ME, Falconi M, Caccuri AM, Desideri A (сентябрь 2001 г.). «Сверхэффективные ферменты». Cellular and Molecular Life Sciences . 58 (10): 1451–1460. doi :10.1007/PL00000788. PMC 11337273. PMID 11693526. S2CID 24874575 .
- ^ Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R (май 2011 г.). «Умеренно эффективный фермент: эволюционные и физико-химические тенденции, формирующие параметры фермента». Биохимия . 50 (21): 4402–4410. doi :10.1021/bi2002289. PMID 21506553.
- ^ Уолш Р., Мартин Э., Дарвеш С. (январь 2010 г.). «Метод описания реакций, катализируемых ферментами, путем объединения параметров кинетики стационарного состояния и хода ферментов». Biochimica et Biophysica Acta (BBA) - General Subjects . 1800 (1): 1–5. doi :10.1016/j.bbagen.2009.10.007. PMID 19840832.
- ^ Beal SL (декабрь 1983 г.). «Вычисление явного решения уравнения Михаэлиса-Ментен». Журнал фармакокинетики и биофармацевтики . 11 (6): 641–657. doi :10.1007/BF01059062. PMID 6689584. S2CID 32571415.
- ^ Шнелл С., Мендоса С. (1997). «Закрытая форма решения для зависящей от времени ферментативной кинетики». Журнал теоретической биологии . 187 (2): 207–212. Bibcode : 1997JThBi.187..207S. doi : 10.1006/jtbi.1997.0425.
- ^ Goudar CT, Sonnad JR, Duggleby RG (январь 1999). «Оценка параметров с использованием прямого решения интегрированного уравнения Михаэлиса-Ментен» (PDF) . Biochimica et Biophysica Acta (BBA) - Структура белка и молекулярная энзимология . 1429 (2): 377–383. doi :10.1016/s0167-4838(98)00247-7. PMID 9989222. Архивировано из оригинала (PDF) 9 ноября 2015 г.
- ^ Goudar CT, Harris SK, McInerney MJ, Suflita JM (декабрь 2004 г.). «Анализ кривой прогресса для ферментативных и микробных кинетических реакций с использованием явных решений на основе функции Ламберта W». Журнал микробиологических методов . 59 (3): 317–326. doi :10.1016/j.mimet.2004.06.013. PMID 15488275.
- ^ Berberan-Santos MN (2010). "Общая трактовка ферментативной кинетики Анри Михаэлиса Ментена: точное решение ряда и приближенные аналитические решения" (PDF) . MATCH Communications in Mathematical and in Computer Chemistry . 63 : 283.
- ^ Jones ME (декабрь 1992 г.). «Анализ алгебраических взвешенных оценок наименьших квадратов для параметров фермента». The Biochemical Journal . 288 (Pt 2) (Pt 2): 533–538. doi :10.1042/bj2880533. PMC 1132043. PMID 1463456 .
- ^ Tseng SJ, Hsu JP (август 1990). "Сравнение процедур оценки параметров для модели Михаэлиса-Ментен". Журнал теоретической биологии . 145 (4): 457–464. Bibcode :1990JThBi.145..457T. doi :10.1016/S0022-5193(05)80481-3. PMID 2246896.
- ^ Bravo IG, Busto F, De Arriaga D, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (сентябрь 2001 г.). «Нормализованный график как новый и экономящий время инструмент в комплексном ферментативном кинетическом анализе». The Biochemical Journal . 358 (Pt 3): 573–583. doi :10.1042/bj3580573. PMC 1222113 . PMID 11577687.
- ^ Алмаас Э., Ковач Б., Вичек Т., Олваи З.Н., Барабаши А.Л. (февраль 2004 г.). «Глобальная организация метаболических потоков у бактерии Escherichia coli». Природа . 427 (6977): 839–843. arXiv : q-bio/0403001 . Бибкод : 2004Natur.427..839A. дои : 10.1038/nature02289. PMID 14985762. S2CID 715721.
- ^ Reed JL, Vo TD, Schilling CH, Palsson BO (2003). "Расширенная модель масштаба генома Escherichia coli K-12 (iJR904 GSM/GPR)". Genome Biology . 4 (9): R54. doi : 10.1186/gb-2003-4-9-r54 . PMC 193654. PMID 12952533 .
- ^ для полного вывода см. здесь
- ^ Dirr H, Reinemer P, Huber R (март 1994). "Рентгеновские кристаллические структуры цитозольных глутатион S-трансфераз. Последствия для архитектуры белков, распознавания субстратов и каталитической функции". European Journal of Biochemistry . 220 (3): 645–661. doi :10.1111/j.1432-1033.1994.tb18666.x. PMID 8143720.
- ^ Stone SR, Morrison JF (июль 1988). «Дигидрофолатредуктаза из Escherichia coli: кинетический механизм с НАДФН и восстановленным ацетилпиридин адениндинуклеотид фосфатом в качестве субстратов». Биохимия . 27 (15): 5493–5499. doi :10.1021/bi00415a016. PMID 3052577.
- ^ Фишер П. А. (1994). Энзимологический механизм репликативных ДНК-полимераз у высших эукариот. Прогресс в исследовании нуклеиновых кислот и молекулярной биологии. Т. 47. С. 371–97. doi :10.1016/S0079-6603(08)60257-3. ISBN 978-0-12-540047-3. PMID 8016325.
- ^ Акерман С.Е., Мюллер С. (август 2003 г.). «2-Cys пероксиредоксин PfTrx-Px1 участвует в антиоксидантной защите Plasmodium falciparum». Молекулярная и биохимическая паразитология . 130 (2): 75–81. doi :10.1016/S0166-6851(03)00161-0. PMID 12946843.
- ^ Браво И.Г., Барралло С., Ферреро М.А., Родригес-Апарисио Л.Б., Мартинес-Бланко Х., Реглеро А. (сентябрь 2001 г.). «Кинетические свойства ацилнейраминацитидилилтрансферазы Pasteurella haemolytica A2». Биохимический журнал . 358 (Часть 3): 585–598. дои : 10.1042/bj3580585. ПМЦ 1222114 . ПМИД 11577688.
- ^ Kraut J (1977). «Сериновые протеазы: структура и механизм катализа». Annual Review of Biochemistry . 46 : 331–358. doi :10.1146/annurev.bi.46.070177.001555. PMID 332063.
- ^ Cornish-Bowden A (2012). Fundamentals of Enzyme Kinetics . Wiley-Blackwell.
Некоторые ферменты являются гораздо более эффективными катализаторами для одного направления, чем для другого. В качестве яркого примера, предельные скорости прямой реакции, катализируемой метионин аденозилтрансферазой, примерно на 10
5
больше, чем для обратного направления, хотя константа равновесия близка к единице (стр. 59).
- ^ Ricard J, Cornish-Bowden A (июль 1987). «Кооперативные и аллостерические ферменты: 20 лет спустя». European Journal of Biochemistry . 166 (2): 255–272. doi : 10.1111/j.1432-1033.1987.tb13510.x . PMID 3301336.
- ^ Ward WH, Fersht AR (июль 1988). «Тирозил-тРНК-синтетаза действует как асимметричный димер при зарядке тРНК. Обоснование активности половины сайтов». Биохимия . 27 (15): 5525–5530. doi :10.1021/bi00415a021. PMID 3179266.
- ^ Helmstaedt K, Krappmann S, Braus GH (сентябрь 2001 г.). «Аллостерическая регуляция каталитической активности: аспартаттранскарбамоилаза Escherichia coli против хоризматмутазы дрожжей». Microbiology and Molecular Biology Reviews . 65 (3): 404–21, оглавление. doi :10.1128/MMBR.65.3.404-421.2001. PMC 99034 . PMID 11528003.
- ^ Schirmer T, Evans PR (январь 1990). «Структурная основа аллостерического поведения фосфофруктокиназы». Nature . 343 (6254): 140–145. Bibcode :1990Natur.343..140S. doi :10.1038/343140a0. PMID 2136935. S2CID 4272821.
- ^ Хилл AV (1910). «Возможные эффекты агрегации молекул гемоглобина на кривые его диссоциации». J. Physiol . 40 : iv–vii.
- ^ Hartley BS, Kilby BA (февраль 1954). «Реакция п-нитрофениловых эфиров с химотрипсином и инсулином». The Biochemical Journal . 56 (2): 288–297. doi :10.1042/bj0560288. PMC 1269615. PMID 13140189 .
- ^ ab Фершт, Алан (1999). Структура и механизм в науке о белках: руководство по ферментативному катализу и сворачиванию белков . Сан-Франциско: WH Freeman. ISBN 978-0-7167-3268-6.
- ^ Bender ML, Begue-Cantón ML, Blakeley RL, Brubacher LJ, Feder J, Gunter CR и др. (декабрь 1966 г.). «Определение концентрации растворов гидролитических ферментов: альфа-химотрипсин, трипсин, папаин, эластаза, субтилизин и ацетилхолинэстераза». Журнал Американского химического общества . 88 (24): 5890–5913. doi :10.1021/ja00976a034. PMID 5980876.
- ^ Cleland WW (январь 2005 г.). «Использование изотопных эффектов для определения механизмов ферментов». Архивы биохимии и биофизики . 433 (1): 2–12. doi :10.1016/j.abb.2004.08.027. PMID 15581561.
- ^ Northrop DB (1981). «Выражение изотопных эффектов в реакциях, катализируемых ферментами». Annual Review of Biochemistry . 50 : 103–131. doi : 10.1146/annurev.bi.50.070181.000535. PMID 7023356.
- ^ Baillie TA, Rettenmeier AW (1986). «Биотрансформация лекарств: механистические исследования со стабильными изотопами». Журнал клинической фармакологии . 26 (6): 448–451. doi :10.1002/j.1552-4604.1986.tb03556.x. PMID 3734135. S2CID 39193680.
- ^ Cleland WW (1982). «Использование изотопных эффектов для выяснения механизмов ферментов». CRC Critical Reviews in Biochemistry . 13 (4): 385–428. doi :10.3109/10409238209108715. PMID 6759038.
- ^ Christianson DW , Cox JD (1999). «Катализ активированным металлом гидроксидом в цинковых и марганцевых металлоферментах». Annual Review of Biochemistry . 68 : 33–57. doi :10.1146/annurev.biochem.68.1.33. PMID 10872443.
- ^ Kraut DA, Carroll KS, Herschlag D (2003). «Проблемы в механизме ферментов и энергетике». Annual Review of Biochemistry . 72 : 517–571. doi :10.1146/annurev.biochem.72.121801.161617. PMID 12704087.
- ^ Уолш Р., Мартин Э., Дарвеш С. (декабрь 2011 г.). «Ограничения традиционных классификаций ингибиторов». Интегративная биология . 3 (12): 1197–1201. doi :10.1039/c1ib00053e. PMID 22038120.
- ^ Cleland WW (февраль 1963 г.). «Кинетика ферментативно-катализируемых реакций с двумя или более субстратами или продуктами. III. Прогнозирование начальной скорости и паттернов ингибирования путем осмотра». Biochimica et Biophysica Acta . 67 : 188–196. doi :10.1016/0006-3002(63)91816-x. PMID 14021669.
- ^ Уолш Р., Мартин Э., Дарвеш С. (май 2007 г.). «Универсальное уравнение для описания обратимого ингибирования фермента и кинетики активации: моделирование бета-галактозидазы и бутирилхолинэстеразы». Biochimica et Biophysica Acta (BBA) - General Subjects . 1770 (5): 733–746. doi :10.1016/j.bbagen.2007.01.001. PMID 17307293.
- ^ Koshland DE (февраль 1958). «Применение теории специфичности ферментов к синтезу белков». Труды Национальной академии наук Соединенных Штатов Америки . 44 (2): 98–104. Bibcode : 1958PNAS... 44 ...98K. doi : 10.1073/pnas.44.2.98 . PMC 335371. PMID 16590179.
- ^ Hammes GG (июль 2002 г.). «Множественные конформационные изменения в ферментативном катализе». Биохимия . 41 (26): 8221–8228. doi :10.1021/bi0260839. PMID 12081470.
- ^ Sutcliffe MJ, Scrutton NS (июль 2002 г.). «Новая концептуальная основа для ферментативного катализа. Туннелирование водорода в сочетании с динамикой ферментов в ферментах флавопротеинов и хинопротеинов». European Journal of Biochemistry . 269 (13): 3096–3102. doi :10.1046/j.1432-1033.2002.03020.x. PMID 12084049.
- ^ Анри V (1902). «Общая теория действия некоторых диастазов». Компет. Ренд. акад. наук. Париж . 135 : 916–9.
- ^ Соренсен PL (1909). «Enzymstudien {II}. Über die Messung und Bedeutung der Wasserstoffionenkonzentration bei enzymatischen Prozessen» [Ферментные исследования III: Об измерении и значении концентрации ионов водорода в ферментативных процессах]. Биохим. З. (на немецком языке). 21 : 131–304.
- ^ Михаэлис Л., Ментен М. (1913). "Die Kinetik der Invertinwirkung" [Кинетика действия инвертазы]. Biochem. Z. (на немецком языке). 49 : 333–369.; Михаэлис Л., Ментен М.Л., Джонсон К.А., Гуди Р.С. (октябрь 2011 г.). «Оригинальная константа Михаэлиса: перевод статьи Михаэлиса-Ментен 1913 г.». Биохимия . 50 (39): 8264–8269. doi :10.1021/bi201284u. PMC 3381512. PMID 21888353 .
- ^ Бриггс GE, Холдейн Дж. Б. (1925). «Заметка о кинетике действия ферментов». Биохимический журнал . 19 (2): 338–339. doi :10.1042/bj0190338. PMC 1259181. PMID 16743508 .
- ^ Flomenbom O, Velonia K, Loos D, Masuo S, Cotlet M, Engelborghs Y и др. (февраль 2005 г.). «Растянутый экспоненциальный спад и корреляции в каталитической активности флуктуирующих одиночных молекул липазы». Труды Национальной академии наук Соединенных Штатов Америки . 102 (7): 2368–2372. Bibcode : 2005PNAS..102.2368F. doi : 10.1073/pnas.0409039102 . PMC 548972. PMID 15695587 .
- ^ English BP, Min W, van Oijen AM, Lee KT, Luo G, Sun H, et al. (Февраль 2006). «Ever-fluctuating single genetic Molecules: Michaelis-Menten equation revisited». Nature Chemical Biology . 2 (2): 87–94. doi :10.1038/nchembio759. PMID 16415859. S2CID 2201882.
- ^ Lu HP, Xun L, Xie XS (декабрь 1998 г.). «Ферментативная динамика одиночной молекулы». Science . 282 (5395): 1877–1882. Bibcode :1998Sci...282.1877P. doi :10.1126/science.282.5395.1877. PMID 9836635.
- ^ Xue X, Liu F, Ou-Yang ZC (сентябрь 2006 г.). "Уравнение Михаэлиса-Ментен для одной молекулы за пределами квазистатического беспорядка". Physical Review E. 74 ( 3 Pt 1): 030902. arXiv : cond-mat/0604364 . Bibcode : 2006PhRvE..74c0902X. doi : 10.1103/PhysRevE.74.030902. PMID 17025584. S2CID 41674948.
- ^ Bevc S, Konc J, Stojan J, Hodošček M, Penca M, Praprotnik M, Janežič D (2011). "ENZO: веб-инструмент для вывода и оценки кинетических моделей реакций, катализируемых ферментами". PLOS ONE . 6 (7): e22265. Bibcode :2011PLoSO...622265B. doi : 10.1371/journal.pone.0022265 . PMC 3139599 . PMID 21818304. сервер ЭНЗО
Дальнейшее чтение
Вводный
- Корниш-Боуден А. (2012). Основы кинетики ферментов (4-е изд.). Weinheim: Wiley-Blackwell. ISBN 978-3-527-33074-4.
- Стивенс Л., Прайс NC (1999). Основы энзимологии: клеточная и молекулярная биология каталитических белков . Оксфорд [Оксфордшир]: Oxford University Press. ISBN 978-0-19-850229-6.
- Bugg T (2004). Введение в химию ферментов и коферментов . Кембридж, Массачусетс: Blackwell Publishers. ISBN 978-1-4051-1452-3.
- Segel IH (1993). Кинетика ферментов: поведение и анализ быстрых равновесных и стационарных ферментных систем . Нью-Йорк: Wiley. ISBN 978-0-471-30309-1.
Передовой
- Фершт А. (1999). Структура и механизм в науке о белках: руководство по ферментативному катализу и сворачиванию белков . Сан-Франциско: WH Freeman. ISBN 978-0-7167-3268-6.
- Schnell S, Maini PK (2004). «Столетие ферментативной кинетики: надежность оценок K M и v max ». Комментарии к Theoretical Biology . 8 (2–3): 169–87. CiteSeerX 10.1.1.493.7178 . doi :10.1080/08948550302453.
- Уолш К. (1979). Механизмы ферментативных реакций . Сан-Франциско: WH Freeman. ISBN 978-0-7167-0070-8.
- Cleland WW, Cook P (2007). Кинетика и механизм ферментов . Нью-Йорк: Garland Science. ISBN 978-0-8153-4140-6.
Внешние ссылки
- Анимация ферментного анализа — демонстрирует эффекты манипулирования условиями анализа.
- MACiE — База данных механизмов ферментативных реакций
- ФЕРМЕНТ — База данных номенклатуры ферментов Expasy
- ENZO — Веб-приложение для простого построения и быстрого тестирования кинетических моделей реакций, катализируемых ферментами.
- ExCatDB — База данных каталитических механизмов ферментов
- BRENDA — Обширная база данных ферментов, содержащая субстраты, ингибиторы и схемы реакций.
- САБИО-РК — База данных кинетики реакций
- Исследовательская группа Джозефа Краута, Калифорнийский университет в Сан-Диего — Анимации нескольких механизмов ферментативных реакций
- Символика и терминология в кинетике ферментов — подробное объяснение концепций и терминологии в кинетике ферментов.
- Введение в кинетику ферментов — Доступный набор онлайн-уроков по кинетике ферментов.
- Анимированный учебник по кинетике ферментов — Анимированный учебник со звуком


![{\displaystyle {\ce {ES ->[k_{cat}] E + P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/299f3433b9ca64a864deef13f572a0127a2d14e0)
![{\displaystyle v_{0}={\frac {V_{\max }[{\ce {S}}]}{K_{M}+[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2f1d1e9d417b925f380340d6d3581d4006672f)
![{\displaystyle {\begin{align}K_{M}\ &{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{2}+k_{-1}}{k_{1}}}\approx K_{D}\\V_{\max }\ &{\stackrel {\mathrm {def} }{=}}\ k_{cat}{\ce {[E]}}_{tot}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1714252e04d803899ef6ad5b75c074d0f9ebc50c)
![{\displaystyle d{\ce {[ES]}}/{dt}\;{\overset {!}{=}}\;0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eea1ce2a30471bd05b46fe979bb4f12e365b4d5)
![{\displaystyle {\ce {[E]}}_{\text{tot}}={\ce {[E]}}+{\ce {[ES]}}\;{\overset {!}{= }}\;{\text{const}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c082974766078275f236f456e12426c4ea02fc8)

![{\displaystyle {\ce {[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5909e9989dfe9306325e8dab287928f3c984ee3)

![{\displaystyle [{\ce {S}}]/(K_{M}+[{\ce {S}}])\approx [{\ce {S}}]/K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1befa5e00217f79ed63dc6ba5c6a15d78d5425)
![{\displaystyle {\ce {[E]_{\rm {tot}} \approx [E]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ccda6e543afca4e4287f635c5f1a4931ca93e1)
![{\displaystyle v_{0}\approx {\frac {k_{cat}}{K_{M}}}{\ce {[E][S]}}\qquad \qquad {\text{if }}[{\ce {S}}]\ll K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/596b2c4659de250ffbd0b65c085402f9fd16735d)





![{\displaystyle [S]=[S]_{0}(1-k)^{t}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93211e467eb88a4ed3ce4b1b8a64f3645c540709)
![{\displaystyle [S]=[S]_{0}(1-v/[S]_{0})^{t}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc767ed4ec3fb17dbb2b342b438ca22f3a0c5e15)
![{\displaystyle [S]=[S]_{0}(1-(V_{\max }[S]_{0}/(K_{M}+[S]_{0})/[S]_{0}))^{t}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/550cebc162d8baf678f05a64c8435882eba78bfb)
![{\displaystyle {\frac {[S]}{K_{M}}}=W\left[F(t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbfb88da686a3b0298417f08709f60c89538b35e)
![{\displaystyle F(t)={\frac {[S]_{0}}{K_{M}}}\exp \!\left({\frac {[S]_{0}}{K_{M}}}-{\frac {V_{\max }}{K_{M}}}\,t\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39737501b38ca63037f8350456c777481706c602)
![{\displaystyle {\frac {[S]}{K_{M}}}=W\left[F(t)\right]-{\frac {V_{\max }}{k_{cat}K_{M}}}\ {\frac {W\left[F(t)\right]}{1+W\left[F(t)\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/036e38cefdac7ce988899ea0d4b89f80c0b6e81d)
![{\displaystyle {\frac {1}{v}}={\frac {K_{M}}{V_{\max }[{\mbox{S}}]}}+{\frac {1}{V_{ \макс }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f67c173c3e3e8c78da7dc5fa15c3b5ff299e4439)
![{\displaystyle {\ce {{E}+S<=>[k_{1}][k_{-1}]ES->[k_{2}]EI->[k_{3}]{E}+ П}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cd1904bee27689d5df0933e40a4b01631243041)
![{\displaystyle v_{0}=k_{cat}{\frac {{\ce {[S] [E]_0}}}{K_{M}^{\prime }+{\ce {[S]}} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90d4c1b92e79705a9ecf0f8615982c0bc91f4a3)





![{\displaystyle {\ce {\overset {}{E->[{\ce {A \atop \downarrow }}]EA<=>E^{\ast }P->[{\ce {P \atop \uparrow }}]E^{\ast }->[{\ce {B \atop \downarrow }}]E^{\ast }B<=>EQ->[{\ce {Q \atop \uparrow }}]E}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b768dbbd547267c22748f29590cb0a639375de)
![{\displaystyle {\ce {{E}+{S}<=>[k_{1}][k_{-1}]ES<=>[k_{2}][k_{-2}]{E} +{P}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe362b85b97b0614f6139dd0be2e8389a2c3b63e)
![{\displaystyle v_{0}={\frac {d\,[{\rm {P}}]}{dt}}={\frac {(k_{1}k_{2}\,[{\rm {S}}]-k_{-1}k_{-2}[{\rm {P}}])[{\rm {E}}]_{0}}{k_{-1}+k_{2}+k_{1}\,[{\rm {S}}]+k_{-2}\,[{\rm {P}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01297c24d81598b7438d064174294408dacc5e60)


![{\displaystyle {\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {k_{1}k_{2}}{k_{-1}k_{-2}}}=K_{\rm {eq}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0ca30bfb4f852fcc02a12f729bcbd3adc500d6)
![{\displaystyle [{\rm {S}}]\rightarrow \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e69387ec816688807461db5902b440a6a65ed0)
![{\displaystyle [{\rm {P}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c498e9bfae3b2d0f1378c8a1a15031f4002279)
![{\displaystyle [{\rm {S}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ac89660d3f5c0ad06eac244190defc17cd7a61)
![{\displaystyle [{\rm {P}}]\rightarrow \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/020c2fe953abd3c508b7bd3a6d97bb29225faeeb)
![{\displaystyle V_{\rm {макс}}^{f}=k_{2}{\rm {[E]}}_{общ}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1834ca7ac4c486ffc3e1c89742f31c266797da98)
![{\displaystyle V_{\rm {макс}}^{b}=-k_{-1}{\rm {[E]}}_{общ}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09363446309c8c26702430b70bfec463a3b0134)


![{\displaystyle K_{\rm {eq}}={\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {V_{\rm {max}}^{f}/K_{M}^{S}}{V_{\rm {max}}^{b}/K_{M}^{P}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/621e1b38683241916244c9e90f5625f14f1f0088)


![{\displaystyle {\cfrac {V_{\max }}{1+{\cfrac {[I]}{K_{i}}}}} = {\cfrac {V_{\max }}{\cfrac {[I ]+K_{i}}{K_{i}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c58cef49731511f5011822f1e92d4da22814891)
![{\displaystyle {\cfrac {V_{\max}}{\cfrac {[I]+K_{i}}{[I]+K_{i}-[I]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42e34b0927bf9484b8a664e022d3fd6ba0ad2326)
![{\displaystyle {\cfrac {V_{\max}}{\cfrac {1}{1-{\cfrac {[I]}{[I]+K_{i}}}}}}=V_{\max}-V_{\max}{\cfrac {[I]}{[I]+K_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4132fbd61b7474f8e3ef391f82d1d196a2a325ff)
![{\displaystyle V_{\max }-\Delta V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90f5601fefd8114c165ac3dfb739e0642e62610c)
![{\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[I]}{[I]+K_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c31b5f56aaeed122d1f8a67491c56d272686b6e)
![{\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[X]}{[X]+K_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bb687fca77a00dba879a00fb32b7ca1bc867973)
![{\displaystyle K_{m1}-(K_{m1}-K_{m2}){\cfrac {[X]}{[X]+K_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a298dbb441e88b96a618cc31df3aaebac17d85)