Элементарные режимы
Набор простейших путей в биохимической сети

В биохимии элементарные моды [1] можно считать минимальными реализуемыми моделями потоков через биохимическую сеть , которые могут поддерживать устойчивое состояние . Это означает, что элементарные моды не могут быть далее разложены на более простые пути. Все возможные потоки через сеть могут быть построены из линейных комбинаций элементарных мод.

Набор элементарных мод для данной сети уникален (с точностью до произвольного масштабного коэффициента). Учитывая фундаментальную природу элементарных мод в отношении уникальности и неразложимости, термин «путь» можно определить как элементарный режим. Обратите внимание, что набор элементарных мод будет меняться по мере изменения набора экспрессируемых ферментов при переходах из одного состояния клетки в другое. Математически набор элементарных мод определяется как набор векторов потока , которые удовлетворяют условию устойчивого состояния v {\displaystyle \mathbf {v} }

N   v ( x , p ) = 0 {\displaystyle \mathbf {N} \ \mathbf {v} (\mathbf {x} ,\mathbf {p} )=0}

где — матрица стехиометрии , — вектор скоростей , — вектор стационарных плавающих (или внутренних) частиц и — вектор параметров системы . N {\displaystyle \mathbf {N} } v {\displaystyle \mathbf {v} } x {\displaystyle \mathbf {x} } p {\displaystyle \mathbf {p} }

Важным условием является то, что скорость каждой необратимой реакции должна быть неотрицательной, v i r r ≥ 0. {\displaystyle \mathbf {v} _{irr}\geq 0.}

Более формальное определение дается следующим образом: [2]

Элементарная мода, , определяется как вектор потоков, , такой, что выполняются три условия, перечисленные в следующих критериях. v i {\displaystyle \mathbf {v} _{i}} v 1 , v 2 , … {\displaystyle v_{1},v_{2},\ldots }

  1. Вектор должен удовлетворять: , то есть: условию устойчивого состояния. v i {\displaystyle \mathbf {v} _{i}} N v i = 0 {\displaystyle \mathbf {N} \mathbf {v} _{i}=0}
  2. Для всех необратимых реакций: . Это означает, что все модели течения должны использовать реакции, которые протекают в их наиболее естественном направлении. Это делает путь, описанный элементарной модой, термодинамически возможным путем. v i ≥ 0 {\displaystyle v_{i}\geq 0}
  3. Вектор должен быть элементарным. То есть, его нельзя сгенерировать, объединив два других вектора, которые удовлетворяют первому и второму требованиям, используя тот же набор ферментов, которые появляются как ненулевые записи в . Другими словами, его нельзя разложить на два других пути, которые сами по себе могут поддерживать устойчивое состояние. Это называется элементарностью. Более формальный тест заключается в том, что нулевое пространство подматрицы , которая включает только реакции , имеет размерность один и не имеет нулевых записей. [2] v i {\displaystyle \mathbf {v} _{i}} v i {\displaystyle \mathbf {v} _{i}} v i {\displaystyle \mathbf {v} _{i}} v i {\displaystyle \mathbf {v} _{i}} N {\displaystyle \mathbf {N} } v i {\displaystyle \mathbf {v} _{i}}

Пример

Рассмотрим простой разветвленный путь, в котором все три шага необратимы. Такой путь допускает два элементарных режима, которые обозначены утолщенными (или красными) линиями реакции.

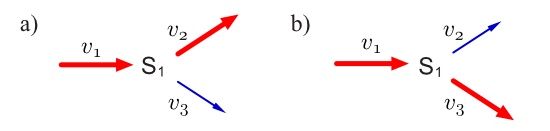
Простой разветвленный путь, в котором все реакции необратимы и содержат всего два элементарных режима
Простой разветвленный путь, в котором все реакции необратимы и содержат всего два элементарных режима

Поскольку и и необратимы, а элементарная мода, лежащая на обеих этих реакциях, невозможна, поскольку это означало бы одну реакцию, идущую против ее термодинамического направления. Каждая мода в этой системе удовлетворяет трем условиям, описанным выше. Первое условие — это стационарное состояние, то есть для каждой моды должно быть верно, что . v 2 {\displaystyle v_{2}} v 3 {\displaystyle v_{3}} v i {\displaystyle \mathbf {v} _{i}} N v i = 0 {\displaystyle \mathbf {N} \mathbf {v} _{i}=0}

Алгебраически эти два режима задаются следующим образом:

v 1 = [ 1 1 0 ] v 2 = [ 1 0 1 ] {\displaystyle \mathbf {v} _{1}={\begin{bmatrix}1\\1\\0\end{bmatrix}}\quad \mathbf {v} _{2}={\begin{bmatrix}1\\0\\1\end{bmatrix}}}

Подставляя каждый из этих векторов в , легко показать, что условие один выполняется. Для условия два мы должны гарантировать, что все реакции, которые являются необратимыми, имеют положительные записи в соответствующих элементах элементарных мод. Поскольку все три реакции в ветви необратимы и все записи в элементарных модах положительны, условие два выполняется. N v i = 0 {\displaystyle \mathbf {N} \mathbf {v} _{i}=0}

Наконец, чтобы удовлетворить условию три, мы должны спросить, можем ли мы разложить два элементарных режима на другие пути, которые могут поддерживать устойчивое состояние, используя те же ненулевые записи в элементарном режиме. В этом примере невозможно разложить элементарные режимы дальше, не нарушив способность поддерживать устойчивое состояние. Поэтому, при выполнении всех трех условий, мы можем заключить, что два вектора, показанные выше, являются элементарными режимами.

Все возможные потоки через сеть могут быть построены из линейных комбинаций элементарных мод, то есть:

v = ∑ λ i v i where λ ≥ 0 {\displaystyle {\begin{aligned}\mathbf {v} &=\sum \lambda _{i}\mathbf {v} _{i}\\{\mbox{where}}&\\\lambda &\geq 0\\\end{aligned}}}

таким образом, чтобы можно было описать все пространство потоков через сеть. должно быть больше или равно нулю, чтобы гарантировать, что необратимые шаги не будут непреднамеренно направлены в обратном направлении. Например, ниже приведен возможный стационарный поток в разветвленном пути. λ i {\displaystyle \lambda _{i}}

v = 2.5 [ 1 1 0 ] + 0.5 [ 1 0 1 ] = [ 3.0 2.5 0.5 ] {\displaystyle v=2.5{\begin{bmatrix}1\\1\\0\end{bmatrix}}+0.5{\begin{bmatrix}1\\0\\1\end{bmatrix}}={\begin{bmatrix}3.0\\2.5\\0.5\end{bmatrix}}}

Если один из этапов оттока в простом разветвленном пути сделать обратимым, становится доступным дополнительный элементарный режим, представляющий поток между двумя ветвями оттока. Дополнительный режим возникает, поскольку, имея только первые два режима, невозможно представить поток между двумя ветвями, поскольку масштабный коэффициент, , не может быть отрицательным (что потребовалось бы для изменения направления потока). λ i {\displaystyle \lambda _{i}}

Определение пути

Страница Википедии Метаболический путь определяет путь как «метаболический путь — это связанная серия химических реакций, происходящих внутри клетки». Это означает, что любая последовательность реакций может быть обозначена как метаболический путь. Однако по мере того, как метаболизм был раскрыт, группам реакций были присвоены определенные метки, такие как гликолиз , цикл Кребса или биосинтез серина . Часто категоризация основывалась на общей химии или идентификации входа и выхода. Например, биосинтез серина начинается с 3-фосфоглицерата и заканчивается серином. Это несколько ad hoc средство для определения путей, особенно когда пути представляют собой динамические структуры, изменяющиеся в результате изменения окружающей среды при изменении экспрессии генов. Например, цикл Кребса часто не является циклическим, как это изображается в учебниках. У E. coli и других бактерий он является циклическим только во время аэробного роста на ацетате или жирных кислотах. [3] Вместо этого в условиях анаэробиоза его ферменты функционируют как два отдельных биосинтетических пути, производя сукцинил-КоА и α-кетоглутарат.

Поэтому было предложено [4] определять путь как один элементарный режим или некоторую комбинацию элементарных режимов. Дополнительным преимуществом является то, что набор элементарных режимов уникален и неразложим на более простые пути. Поэтому один элементарный режим можно рассматривать как элементарный путь. Обратите внимание, что набор элементарных режимов будет меняться по мере изменения набора экспрессируемых ферментов при переходах из одного состояния клетки в другое.

Таким образом, элементарные моды дают однозначное определение пути.

Комментарий к Условию Три

Условие три относится к неразложимости элементарного режима и отчасти делает элементарные режимы интересными. Две другие важные особенности, как указано ранее, — это уникальность пути и термодинамическая правдоподобность. Разложение подразумевает, что можно представить режим как комбинацию двух или более других режимов. Например, режим может быть составлен из двух других режимов, и : e 1 {\displaystyle \mathbf {e} _{1}} e 2 {\displaystyle \mathbf {e} _{2}} e 3 {\displaystyle \mathbf {e} _{3}}

e 1 = λ 1 e 2 + λ 2 e 3 {\displaystyle \mathbf {e} _{1}=\lambda _{1}\mathbf {e} _{2}+\lambda _{2}\mathbf {e} _{3}}

Если моду можно разложить, означает ли это, что мода не является элементарной модой? Условие три предоставляет правило для определения, означает ли разложение, что данная мода является элементарной модой или нет. Если возможно разложить данную моду только путем введения ферментов, которые не используются в моде, то мода является элементарной. То есть, существует ли более одного способа создать путь (т. е. что-то, что может поддерживать устойчивое состояние) с ферментами, которые в настоящее время используются в моде? Если да, то мода не является элементарной. Чтобы проиллюстрировать это тонкое условие, рассмотрим путь, показанный ниже.

Стилизованная карта путей гликолиза.
Стилизованная карта путей гликолиза.

Этот путь представляет собой стилизованное изображение гликолиза. Шаги три и шесть обратимы и соответствуют триозофосфатизомеразе и глицерол-3-фосфатдегидрогеназе соответственно.

Сеть имеет четыре элементарных режима потока, которые показаны на рисунке ниже.

Стилизованная карта путей гликолиза.
Стилизованная карта путей гликолиза.

Векторы элементарных мод потока показаны ниже:

  e 1     e 2 e 3 e 4 [ − 0 − 1 − 1 − 1 − 0 − 1 − 1 − 1 − 1 − 1 − 1 − 0 − 1 − 0 − 2 − 1 − 1 − 0 − 2 − 1 − 1 − 2 − 0 − 1 ] {\displaystyle {\begin{array}{l}\qquad \ \mathbf {e} _{1}\quad \ \ \mathbf {e} _{2}\quad \mathbf {e} _{3}\quad \mathbf {e} _{4}\\{\begin{bmatrix}&{\phantom {-}}0&{\phantom {-}}1&{\phantom {-}}1&{\phantom {-}}1\\&{\phantom {-}}0&{\phantom {-}}1&{\phantom {-}}1&{\phantom {-}}1\\&{\phantom {-}}1&-1&{\phantom {-}}1&{\phantom {-}}0\\&{\phantom {-}}1&{\phantom {-}}0&{\phantom {-}}2&{\phantom {-}}1\\&{\phantom {-}}1&{\phantom {-}}0&{\phantom {-}}2&{\phantom {-}}1\\&-1&{\phantom {-}}2&{\phantom {-}}0&{\phantom {-}}1\\\end{bmatrix}}\\\end{array}}}

Обратите внимание, что в наборе элементарных мод возможны отрицательные записи, поскольку они будут соответствовать обратимым шагам. Интересно наблюдение, что четвертый вектор (где представляет транспонирование) может быть сформирован из суммы первого и второго векторов. Это говорит о том, что четвертый вектор не является элементарной модой. e 4 = [ 1   1   0   1   1   1   ] T {\displaystyle e_{4}=[1\ 1\ 0\ 1\ 1\ 1\ ]^{T}} T {\displaystyle T}

e 4 [ − 1 − − 1 − − 0 − − 1 − − 1 − − 1 − ] = e 1 [ − 0 − − 0 − − 1 − − 1 − − 1 − − 1 − ] + e 2 [ − 1 − − 1 − − 1 − − 0 − − 0 − − 2 − ] {\displaystyle \mathbf {e} _{4}{\begin{bmatrix}{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}0{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\\end{bmatrix}}=\mathbf {e} _{1}{\begin{bmatrix}{\phantom {-}}0{\phantom {-}}\\{\phantom {-}}0{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\-1{\phantom {-}}\\\end{bmatrix}}+\mathbf {e} _{2}{\begin{bmatrix}{\phantom {-}}1{\phantom {-}}\\{\phantom {-}}1{\phantom {-}}\\-1{\phantom {-}}\\{\phantom {-}}0{\phantom {-}}\\{\phantom {-}}0{\phantom {-}}\\{\phantom {-}}2{\phantom {-}}\\\end{bmatrix}}}

Однако это разложение работает только потому, что мы ввели новый фермент (триозофосфатизомеразу), который не используется в . Фактически невозможно разложить на пути, которые могут поддерживать устойчивое состояние, используя только пять шагов, , в элементарном режиме. Поэтому мы заключаем, что это элементарный режим. E 4 {\displaystyle E_{4}} e 4 {\displaystyle \mathbf {e} _{4}} e 4 {\displaystyle \mathbf {e} _{4}} e 1 , e 2 , e 4 , e 5   and   e 6 {\displaystyle e_{1},e_{2},e_{4},e_{5}\ {\mbox{and}}\ e_{6}} e 4 {\displaystyle \mathbf {e} _{4}}

Смотрите также

Ссылки

  1. ^ Зангеллини, Юрген; Рюкербауэр, Дэвид Э.; Ханшо, Михаэль; Юнгрейтмайер, Кристиан (сентябрь 2013 г.). «Элементарные режимы потока в двух словах: свойства, расчет и применение». Biotechnology Journal . 8 (9): 1009–1016. doi : 10.1002/biot.201200269 . PMID  23788432.
  2. ^ ab Бедасо, Йосеф; Бергманн, Фрэнк Т.; Чой, Кири; Сауро, Герберт М. (3 мая 2018 г.). «Переносимая библиотека структурного анализа для сетей реакций»: 245068. doi : 10.1101/245068. S2CID  46925656. {{cite journal}}: Цитировать журнал требует |journal=( помощь ) Текст скопирован из этого источника, который доступен по лицензии Creative Commons Attribution 4.0 International.
  3. ^ Escherichia coli и Salmonella: клеточная и молекулярная биология (2-е изд.). Вашингтон, округ Колумбия: ASM Press. 1996. ISBN 1555810845.
  4. ^ Шустер, Стефан; Фелл, Дэвид А.; Дандекар, Томас (март 2000 г.). «Общее определение метаболических путей, полезное для систематической организации и анализа сложных метаболических сетей». Nature Biotechnology . 18 (3): 326–332. doi :10.1038/73786. PMID  10700151. S2CID  7742485.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Elementary_modes&oldid=1250990063"