Предельная теорема Эджворта

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены. Найти источники:  «Предельная теорема Эджворта» – новости  · газеты  · книги  · ученый  · JSTOR ( февраль 2014 г. ) ( Узнайте, как и когда удалять это сообщение )

Предельная теорема Эджворта — экономическая теорема, названная в честь Фрэнсиса Исидро Эджворта , утверждающая, что ядро ​​экономики сжимается до множества вальрасовских равновесий, когда число агентов увеличивается до бесконечности.

То есть среди всех возможных результатов, которые могут возникнуть в результате свободного рыночного обмена или бартера между группами людей, хотя точное место окончательного расчета (окончательного раздела товаров) между сторонами не определено однозначно, по мере увеличения числа торговцев набор всех возможных окончательных расчетов сходится к набору равновесий Вальраса.

Интуитивно это можно интерпретировать как утверждение о том, что по мере роста экономики агенты все чаще ведут себя так, как будто они принимают цены, даже если у них есть возможность торговаться.

Эджворт (1881) предположил теорему, предоставил большую часть необходимой интуиции и проделал определенный путь к ее доказательству. ^[1] Формальные доказательства были представлены при различных предположениях Дебре и Скарфом (1963) ^[2] , а также Ауманн (1964), ^[3] оба доказали при условиях более строгих, чем те, которые предполагал Эджворт. Дебре и Скарф рассмотрели случай «реплики экономики», где есть конечное число типов агентов, а агенты, добавленные в экономику, чтобы сделать ее «большой», принадлежат к тому же типу и в той же пропорции, что и те, которые уже в ней находятся. Результат Ауманна основывался на существовании континуума агентов .

Ядро экономики — это концепция из теории кооперативных игр, определяемая как набор возможных распределений в экономике, который не может быть улучшен подмножеством множества потребителей экономики (коалицией). Для экономик общего равновесия ядро ​​обычно непустое (существует по крайней мере одно возможное распределение) , но также «большое» в том смысле, что может быть континуум возможных распределений, удовлетворяющих требованиям. Гипотеза в основном утверждает, что если число агентов также «большое», то единственные распределения в ядре — это именно то, что будет производить конкурентный рынок . Таким образом, гипотеза рассматривается как предоставление некоторых теоретико-игровых основ для обычного предположения в теории общего равновесия об агентах, принимающих цены. В частности, это означает, что в «большой» экономике люди действуют так, как если бы они были ценополучателями, хотя теоретически у них есть вся власть устанавливать цены и пересматривать свои сделки. Таким образом, вымышленный вальрасовский аукционист общего равновесия, хотя, строго говоря, совершенно нереалистичен, может рассматриваться как «кратчайший путь» к получению правильного ответа.

Фрэнсис Исидро Эджворт впервые описал то, что позже стало известно как предельная теорема, в своей книге «Математическая психика» (1881). Он использовал вариант того, что сейчас известно как ящик Эджворта (с количествами проданных, а не количествами, которыми владеют, на соответствующих осях) для анализа торговли между группами торговцев разных размеров. В целом он обнаружил, что «контракт без конкуренции неопределен, контракт с совершенной конкуренцией совершенно определен, [и] контракт с более или менее совершенной конкуренцией менее или более неопределен».

Если торговля двумя товарами , X и Y, происходит между одной парой торговцев , A и B, потенциальные результаты этой торговли можно показать в ящике Эджворта ( Рисунок 1 ). На этой диаграмме A и B изначально владеют всем запасом X и Y соответственно (точка E). Линии U(a) и U(b) являются кривыми безразличия A и B, которые проходят через точки, представляющие комбинации товаров, которые дают полезность , равную их первоначальным запасам. Поскольку торговля здесь предполагается не принудительной, ни один из торговцев не согласится на окончательное урегулирование, которое оставит их в худшем положении, чем они начинали, и, таким образом, U(a) и U(b) представляют собой внешние границы возможных урегулирований. Эджворт продемонстрировал, что торговцы в конечном итоге достигнут точки на кривой контракта (между C и C') посредством стилизованного процесса торга, который называется процессом повторного заключения контракта. Поскольку ни один из участников не может стать богаче, не ухудшив положение другого в точках контрактной кривой, как только торговцы соглашаются урегулировать ситуацию в точке на ней, это окончательное урегулирование. Невозможно точно определить, где именно на контрактной кривой будет окончательное урегулирование. Это будет зависеть от процесса переговоров между двумя участниками; сторона, которая сможет получить преимущество в ходе переговоров, сможет получить лучшую цену за свои товары и, таким образом, получить более высокую прибыль от торговли .

Это был ключевой вывод Эджворта: результат торговли между двумя людьми можно предсказать в определенном диапазоне, но точный результат неопределен.

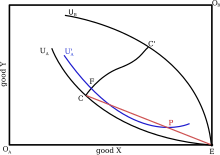
Предположим, что к этой первоначальной паре добавляется одна дополнительная пара идентичных торговцев. Поскольку эти новые торговцы идентичны первой паре, тот же ящик Эджворта может быть использован для анализа обмена. Чтобы изучить новые внешние границы торговли, Эджворт рассмотрел ситуацию, когда торговля происходит на пределе торговли между двумя людьми (точка C или C' на рисунке 2 ). Если бы торговля происходила в точке C, один из B (скажем, B(1)) получил бы все выгоды от торговли. Тот A, который торгует с B(1) (скажем, A(1)) теперь имеет смесь товаров X и Y, которые он может обменять с A(2). Поскольку два A идентичны, они согласятся разделить свои послеторговые запасы поровну между собой, поместив их в точку P на рисунке 2, что дает им более высокую полезность, чем они получили бы в противном случае (кривая безразличия U'(a) вместо U(a)). Теперь у B(2) есть возможность и сильный стимул предложить A лучшую цену за свои товары и торговать с ними по этой цене, оставляя B(1) в стороне. Этот процесс конкуренции B друг с другом за предложение A лучшей цены будет продолжаться до тех пор, пока A не станут безразличны между торговлей по P и торговлей по контрактной кривой ( рисунок 3 ). Те же рассуждения можно применить к случаю, когда A(1) изначально получает всю прибыль от торговли, и можно показать, что самый внешний предел, заданный U(b), также сместится внутрь. Это называется сжимающимся ядром рынка — по мере добавления дополнительной пары трейдеров возможный диапазон сделок сокращается.

Если добавляется третья пара трейдеров, ядро ​​рынка еще больше сжимается. Если торговля происходит на пределе, где B(1) получает всю прибыль от торговли, точка P теперь находится на двух третях пути вдоль линии EC. Это улучшает переговорную силу A, которые могут попасть на более высокую кривую безразличия, поскольку B конкурируют за торговлю с ними. Внешний предел окончательного расчета, где есть несколько пар трейдеров, можно обобщить ( Рисунок 4 ), где K = (n-1)/n.

Если имеется достаточное количество трейдеров, ядро ​​рынка сожмется так, что точка окончательного расчета будет совершенно определена ( Рисунок 5 ). Эта точка равна равновесию ценообразования , при котором, как предполагается, происходит торговля в моделях совершенной конкуренции .

Этот анализ можно модифицировать, чтобы учесть трейдеров, которые не идентичны или имеют мотивы, которые не являются чисто эгоистичными, а также ситуацию, когда одна группа трейдеров больше другой. Если трейдеры неоднородны, точка P не будет отражать торговлю «разделить разницу» между группой трейдеров, и внешний предел торговли, определяемый этой точкой, будет соответствующим образом изменен. Если полезность одного трейдера (трейдеров) влияет на полезность другого (т. е. последний не является эгоистичным), то связанный предел кривой контракта будет сокращаться внутрь, исключая самые несправедливые сделки. Если группы трейдеров имеют разный размер, внешние пределы кривой контракта не будут сокращаться на одинаковую величину.

• Кооперативные переговоры