Покрытие края

В теории графов рёберное покрытие графа — это набор рёбер , такой что каждая вершина графа инцидентна по крайней мере одному ребру набора. В информатике задача минимального рёберного покрытия — это задача нахождения рёберного покрытия минимального размера. Это задача оптимизации , которая относится к классу задач покрытия и может быть решена за полиномиальное время .

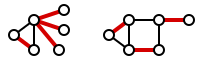
Формально, рёберное покрытие графа G — это множество рёбер C , такое, что каждая вершина в G инцидентна по крайней мере одному ребру в C. Говорят, что множество C покрывает вершины G. На следующем рисунке показаны примеры рёберных покрытий в двух графах (множество C отмечено красным).

Минимальное покрытие рёбер — это покрытие рёбер наименьшего возможного размера. Число покрытия рёбер ρ ( G ) — это размер минимального покрытия рёбер. На следующем рисунке показаны примеры минимальных покрытий рёбер (снова множество C отмечено красным).

Обратите внимание, что рисунок справа — это не только покрытие рёбер, но и паросочетание . В частности, это идеальное паросочетание : паросочетание M , в котором каждая вершина инцидентна ровно одному ребру из M . Идеальное паросочетание (если оно существует) всегда является минимальным покрытием рёбер.

• Множество всех ребер представляет собой реберное покрытие, предполагая, что вершин степени 0 нет.
• Полный двудольный граф K _m,n имеет число реберного покрытия max( m , n ) .

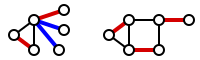
Наименьшее покрытие рёбер можно найти за полиномиальное время , найдя максимальное паросочетание и жадно расширив его так, чтобы были покрыты все вершины. ^{[1] [2]} На следующем рисунке максимальное паросочетание отмечено красным; дополнительные рёбра, которые были добавлены для покрытия несовпавших узлов, отмечены синим. (На рисунке справа показан граф, в котором максимальное паросочетание является идеальным паросочетанием ; следовательно, оно уже покрывает все вершины, и никаких дополнительных рёбер не потребовалось.)

С другой стороны, связанная с этим задача нахождения наименьшего вершинного покрытия является NP-трудной задачей. ^[1]

Глядя на изображение, уже становится очевидным, почему для заданного минимального покрытия рёбер и максимального паросочетания , принимая и за число рёбер в и соответственно, мы имеем: ^[3] . Действительно, содержит максимальное паросочетание, поэтому рёбра из можно разложить на рёбра максимального паросочетания, покрывающие вершины, и другие рёбра, каждое из которых покрывает одну другую вершину. Таким образом, поскольку покрывает все вершины, мы имеем , что даёт искомое равенство.${\displaystyle С}$ ${\displaystyle М}$${\displaystyle с}$${\displaystyle м}$${\displaystyle С}$${\displaystyle М}$ ${\displaystyle |V|=c+m}$${\displaystyle С}$${\displaystyle С}$${\displaystyle м}$${\displaystyle 2м}$${\displaystyle см}$${\displaystyle С}$${\displaystyle |V|}$${\displaystyle |V|=2м+(см)}$

• Крышка вершины
• Задача о покрытии множеств – задача о покрытии рёбер является частным случаем задачи о покрытии множеств: элементы вселенной являются вершинами, и каждое подмножество покрывает ровно два элемента.

• Вайсштейн, Эрик В. «Покрытие кромок». MathWorld .
• Гэри, Майкл Р.; Джонсон , Дэвид С. (1979), Компьютеры и неразрешимость: Руководство по теории NP-полноты , WH Freeman, ISBN 0-7167-1045-5.