Оценщик поля тесселяции Делоне

Оценщик поля тесселяции Делоне (DTFE) (или оценщик поля тесселяции Делоне (DTFE) ) — это математический инструмент для реконструкции объемно-покрывающего и непрерывного поля плотности или интенсивности из дискретного набора точек. DTFE имеет различные астрофизические приложения, такие как анализ численных симуляций формирования космической структуры , картирование крупномасштабной структуры Вселенной и улучшение программ компьютерного моделирования формирования космической структуры. Он был разработан Виллемом Шаапом и Риеном ван де Вейгартом. Главное преимущество DTFE заключается в том, что он автоматически адаптируется к (сильным) изменениям плотности и геометрии. Поэтому он очень хорошо подходит для изучения распределения галактик в больших масштабах.

DTFE состоит из трех основных этапов:

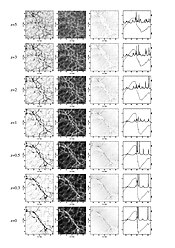
Начальной точкой является заданное дискретное распределение точек. В верхнем левом кадре рисунка построено распределение точек, в центре которого расположен объект, плотность которого радиально уменьшается наружу. На первом шаге DTFE строится мозаика Делоне распределения точек. Это охватывающее объем разделение пространства на треугольники (тетраэдры в трех измерениях), вершины которых образованы распределением точек (см. рисунок, верхний правый кадр). Мозаика Делоне определяется таким образом, что внутри внутренней части описанной окружности каждого треугольника Делоне нет других точек из определяющего распределения точек.

Тесселяция Делоне является сердцем DTFE. На рисунке ясно видно, что тесселяция автоматически адаптируется как к локальной плотности, так и к геометрии распределения точек: где плотность высокая, треугольники маленькие и наоборот. Таким образом, размер треугольников является мерой локальной плотности распределения точек. Это свойство тесселяции Делоне используется на шаге 2 DTFE, на котором локальная плотность оценивается в местах расположения точек выборки. Для этой цели плотность определяется в месте расположения каждой точки выборки как обратная величина площади окружающих ее треугольников Делоне (умноженная на константу нормализации, см. рисунок, нижняя правая рамка).

На шаге 3 эти оценки плотности интерполируются в любую другую точку, предполагая, что внутри каждого треугольника Делоне поле плотности изменяется линейно (см. рисунок, нижняя левая рамка).

Одним из основных применений DTFE является визуализация нашего космического окружения. Ниже показана реконструкция DTFE 2dF Galaxy Redshift Survey , открывающая впечатляющий вид на космические структуры в близлежащей Вселенной. Выделяются несколько сверхскоплений , такие как Sloan Great Wall , одна из крупнейших структур во Вселенной.

• 
  Обзор красного смещения галактики 2dF
• 
  Реконструкция внутренних частей 2dF Galaxy Redshift Survey с помощью DTFE

Большинство алгоритмов для моделирования формирования космических структур являются кодами гидродинамики частиц. В основе этих кодов лежит процедура оценки плотности сглаженной гидродинамики частиц (SPH). Замена ее на оценку плотности DTFE даст значительное улучшение для моделирования, включающего процессы обратной связи, которые играют важную роль в формировании галактик и звезд .

DTFE был разработан для реконструкции полей плотности или интенсивности из дискретного набора нерегулярно распределенных точек, отбирающих это поле. Однако его также можно использовать для реконструкции других непрерывных полей, которые были отобраны в местах расположения этих точек, например, поля космической скорости. Использование DTFE для этой цели имеет те же преимущества, что и для реконструкции полей плотности. Поля реконструируются локально без применения искусственной или зависящей от пользователя процедуры сглаживания , что приводит к оптимальному разрешению и подавлению эффектов дробового шума . Оцененные величины охватывают весь объем и позволяют проводить прямое сравнение с теоретическими предсказаниями.

DTFE был специально разработан для описания сложных свойств космической паутины . Поэтому его можно использовать для изучения эволюции пустот и сверхскоплений в крупномасштабном распределении галактик.

• 
  Эволюция пустоты
• 
  Эволюция сверхскопления

• DTFE: Оценщик поля тесселяции Делоне, Виллем Шаап, 2007 г., докторская диссертация, Рейксуниверситет Гронинген, Нидерланды
• Астрономическая фотография дня НАСА: Великая стена Слоуна: самая большая известная структура? (7 ноября 2007 г.)
• Исследование космических скоростных потоков в локальной Вселенной, Эмилио Романо-Диас, 2004, докторская диссертация, Рейксуниверситет Гронингена, Нидерланды
• Космическая паутина: геометрический анализ, Риен ван де Вейгерт и Виллем Шаап, 2004 г.