последовательность де Брейна

В комбинаторной математике последовательность де Брейна порядка n в алфавите A размера k — это циклическая последовательность , в которой каждая возможная строка длины n в A встречается ровно один раз как подстрока (т. е. как непрерывная подпоследовательность ). Такая последовательность обозначается как B ( k , n ) и имеет длину k n , которая также является числом различных строк длины n в A . Каждая из этих различных строк, взятая как подстрока B ( k , n ) , должна начинаться в другой позиции, поскольку подстроки, начинающиеся в одной и той же позиции, не являются различными. Следовательно, B ( k , n ) должна иметь не менее k n символов. И поскольку B ( k , n ) имеет ровно k n символов , последовательности де Брейна являются оптимально короткими относительно свойства содержать каждую строку длины n хотя бы один раз.
Число различных последовательностей де Брейна B ( k , n ) равно
Для двоичного алфавита это приводит к следующей последовательности для положительных чисел : 1, 1, 2, 16, 2048, 67108864... ( OEIS : A016031 )
Последовательности названы в честь голландского математика Николаса Говерта де Брейна , который писал о них в 1946 году. [1] Как он позже писал, [2] существование последовательностей де Брейна для каждого порядка вместе с указанными выше свойствами было впервые доказано для случая алфавитов с двумя элементами Камиллой Флай Сент-Мари (1894). Обобщение на более крупные алфавиты принадлежит Татьяне ван Аарденне-Эренфест и де Брейну (1951). Автоматы для распознавания этих последовательностей обозначаются как автоматы де Брейна.
Во многих приложениях A = {0,1}.
История
Самый ранний известный пример последовательности де Брейна происходит из санскритской просодии , где, начиная с работы Пингалы , каждому возможному трехсложному шаблону длинных и коротких слогов дается название, например, «y» для короткого-длинного-длинного и «m» для длинного-длинного-длинного. Чтобы запомнить эти названия, используется мнемоническое yamātārājabhānasalagām , в котором каждый трехсложный шаблон начинается с его имени: «yamātā» имеет шаблон короткого-длинного-длинного, «mātārā» имеет шаблон длинного-длинного-длинного и так далее, до «salagām», который имеет шаблон короткого-короткого-длинного. Эта мнемоника, эквивалентная последовательности де Брейна на двоичных тройках, неизвестна по древности, но по крайней мере так же стара, как и книга Чарльза Филиппа Брауна 1869 года о санскритской просодии, в которой она упоминается и рассматривается как «древняя строка, написанная Панини ». [3]
В 1894 году А. де Ривьер поднял вопрос в выпуске французского проблемного журнала L'Intermédiaire des Mathématiciens о существовании кругового расположения нулей и единиц размера , которое содержит все двоичные последовательности длины . Задача была решена (утвердительно), вместе с подсчетом различных решений, Камиллом Флай Сент-Мари в том же году. [2] Это было в значительной степени забыто, и Мартин (1934) доказал существование таких циклов для общего размера алфавита вместо 2, с алгоритмом для их построения. Наконец, когда в 1944 году Кис Постумус предположил подсчет для двоичных последовательностей, де Брейн доказал гипотезу в 1946 году, благодаря чему задача стала широко известной. [2]
Карл Поппер независимо описал эти объекты в своей «Логике научного открытия» (1934), назвав их «кратчайшими случайно-подобными последовательностями». [4]
Примеры
- Принимая A = {0, 1}, получаем два различных B (2, 3): 00010111 и 11101000, одно из которых является обратным или отрицательным значением другого.
- Две из 16 возможных букв B (2, 4) в одном алфавите — это 0000100110101111 и 0000111101100101.
- Две из 2048 возможных букв B (2, 5) в том же алфавите — это 0000010001100101001110101101111 и 00000101001000111110111001101011.
Строительство
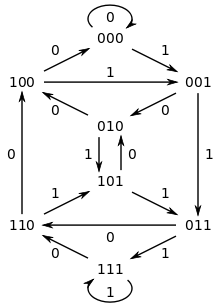
Последовательности де Брейна могут быть построены путем взятия гамильтонова пути n -мерного графа де Брейна над k символами (или, что эквивалентно, эйлерова цикла ( n − 1)-мерного графа де Брейна). [5]
Альтернативная конструкция включает в себя объединение в лексикографическом порядке всех слов Линдона , длина которых делит n . [6]
Обратное преобразование Барроуза-Уиллера может быть использовано для генерации требуемых слов Линдона в лексикографическом порядке. [7]
Последовательности де Брейна также могут быть построены с использованием регистров сдвига [8] или с помощью конечных полей . [9]
Пример использования графика де Брейна

Цель: построить B (2, 4) последовательность де Брейна длины 2 4 = 16, используя эйлеров ( n - 1 = 4 - 1 = 3) трехмерный цикл графа де Брейна.
Каждое ребро в этом трехмерном графе де Брейна соответствует последовательности из четырех цифр: три цифры, которые обозначают вершину, которую покидает ребро, за которыми следует цифра, которая обозначает ребро. Если пройти по ребру, обозначенному 1, от 000, то мы придем к 001, тем самым указывая на наличие подпоследовательности 0001 в последовательности де Брейна. Чтобы пройти каждое ребро ровно один раз, нужно использовать каждую из 16 четырехзначных последовательностей ровно один раз.
Например, предположим, что мы следуем по следующему эйлерову пути через эти вершины:
- 000, 000, 001, 011, 111, 111, 110, 101, 011,
- 110, 100, 001, 010, 101, 010, 100, 000.
Это выходные последовательности длины k :
- 0 0 0 0
- _ 0 0 0 1
- _ _ 0 0 1 1
Это соответствует следующей последовательности де Брейна:
- 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1
Восемь вершин появляются в последовательности следующим образом:
{0 0 0 0} 1 1 1 1 0 1 1 0 0 1 0 1 0 {0 0 0 1} 1 1 1 0 1 1 0 0 1 0 1 0 0 {0 0 1 1} 1 1 0 1 1 0 0 1 0 1 0 0 0 {0 1 1 1} 1 0 1 1 0 0 1 0 1 0 0 0 0 {1 1 1 1} 0 1 1 0 0 1 0 1 0 0 0 0 1 {1 1 1 0} 1 1 0 0 1 0 1 0 0 0 0 1 1 {1 1 0 1} 1 0 0 1 0 1 0 0 0 0 1 1 1 {1 0 1 1} 0 0 1 0 1 0 0 0 0 1 1 1 1 {0 1 1 0} 0 1 0 1 0 0 0 0 1 1 1 1 0 {1 1 0 0} 1 0 1 0 0 0 0 1 1 1 1 0 1 {1 0 0 1} 0 1 0 0 0 0 1 1 1 1 0 1 1 {0 0 1 0} 1 0 0 0 0 1 1 1 1 0 1 1 0 {0 1 0 1} 0} 0 0 0 1 1 1 1 0 1 1 0 0 {1 0 1 ... ... 0 0} 0 0 1 1 1 1 0 1 1 0 0 1 {0 1 ... ... 0 0 0} 0 1 1 1 1 0 1 1 0 0 1 0 {1 ......а затем возвращаемся к исходной точке. Каждая из восьми 3-значных последовательностей (соответствующих восьми вершинам) появляется ровно дважды, а каждая из шестнадцати 4-значных последовательностей (соответствующих 16 ребрам) появляется ровно один раз.
Пример использования обратного преобразования Барроуза—Уиллера
Математически обратное преобразование Барроуза-Уиллера для слова w генерирует мультимножество классов эквивалентности, состоящее из строк и их вращений. [7] Каждый из этих классов эквивалентности строк содержит слово Линдона в качестве уникального минимального элемента, поэтому можно считать, что обратное преобразование Барроуза-Уиллера генерирует множество слов Линдона. Можно показать, что если мы выполним обратное преобразование Барроуза-Уиллера для слова w, состоящего из алфавита размера k, повторенного k n −1 раз (так что это даст слово той же длины, что и желаемая последовательность де Брейна), то результатом будет множество всех слов Линдона, длина которых делит n . Из этого следует, что упорядочивание этих слов Линдона в лексикографическом порядке даст последовательность де Брейна B ( k , n ), и что это будет первая последовательность де Брейна в лексикографическом порядке. Для выполнения обратного преобразования Барроуза—Уиллера можно использовать следующий метод, используя его стандартную перестановку :
- Сортируем символы в строке w , получая новую строку w ′
- Расположите строку w ′ над строкой w и сопоставьте позицию каждой буквы в w ′ с ее позицией в w , сохраняя порядок. Этот процесс определяет стандартную перестановку.
- Запишите эту перестановку в циклической нотации, начиная с наименьшей позиции в каждом цикле, а циклы отсортируйте в порядке возрастания.
- Для каждого цикла замените каждое число соответствующей буквой из строки w ′ в этой позиции.
- Каждый цикл теперь стал словом Линдона, и они расположены в лексикографическом порядке, поэтому, если опустить скобки, получим первую последовательность де Брейна.
Например, чтобы построить наименьшую последовательность B (2,4) де Брейна длины 2 4 = 16, повторите алфавит (ab) 8 раз, получив w =ababababababab . Отсортируйте символы в w , получив w ′ =aaaaaaaabbbbbbb . Расположите w ′ над w , как показано, и сопоставьте каждый элемент в w ′ с соответствующим элементом в w , нарисовав линию. Пронумеруйте столбцы, как показано, чтобы мы могли прочитать циклы перестановки:
Начиная слева направо, циклы записи стандартной перестановки следующие: (1) (2 3 5 9) (4 7 13 10) (6 11) (8 15 14 12) (16) . (Стандартная перестановка)
Затем, заменив каждое число соответствующей буквой в w ′ из этого столбца, получим: (a)(aaab)(aabb)(ab)(abbb)(b) .
Это все слова Линдона, длина которых делится на 4, в лексикографическом порядке, поэтому, опуская скобки, получаем B (2,4) = aaaabaabbababbbb .
Алгоритм
Следующий код Python вычисляет последовательность де Брейна, заданную k и n , на основе алгоритма из «Комбинаторной генерации » Фрэнка Раскея . [10]
из набора import Iterable , Any def de_bruijn ( k : Iterable [ str ] | int , n : int ) -> str : """Последовательность де Брейна для алфавита k и подпоследовательностей длины n. """ # Два вида ввода алфавита: целое число расширяется # до списка целых чисел как алфавита.. if isinstance ( k , int ): alphabet = list ( map ( str , range ( k ))) else : # В то время как любой вид списка становится используемым как он есть alphabet = k k = len ( k ) а = [ 0 ] * к * n последовательность = [] def db ( t , p ): если t > n : если n % p == 0 : последовательность . extend ( a [ 1 : p + 1 ]) иначе : a [ t ] = a [ t - p ] db ( t + 1 , p ) для j в диапазоне ( a [ t - p ] + 1 , k ): a [ t ] = j db ( t + 1 , t ) db ( 1 , 1 ) возвращает "" . join ( алфавит [ i ] для i в последовательности )распечатать ( de_bruijn ( 2 , 3 )) распечатать ( de_bruijn ( «abcd» , 2 ))который печатает
00010111aabacadbbcbdccdd
Обратите внимание, что эти последовательности понимаются как «завернутые» в цикле. Например, первая последовательность содержит 110 и 100 таким образом.
Использует
Циклы де Брейна широко используются в экспериментах по нейронауке и психологии, которые изучают влияние порядка стимула на нейронные системы [11] , и могут быть специально созданы для использования с функциональной магнитно-резонансной томографией [12] .
Распознавание угла
Символы последовательности де Брейна, записанные вокруг круглого объекта (например, колеса робота ) , могут быть использованы для определения его угла путем изучения n последовательных символов, обращенных к фиксированной точке. Эта проблема кодирования угла известна как «проблема вращающегося барабана». [13] Коды Грея могут быть использованы как аналогичные механизмы ротационного позиционного кодирования, метод, обычно встречающийся в ротационных энкодерах .
Поиск наименее или наиболее значимого бита набора в слове
Последовательность де Брейна может быть использована для быстрого нахождения индекса наименее значимого бита набора («самая правая 1») или наиболее значимого бита набора («самая левая 1») в слове с использованием побитовых операций и умножения. [14] В следующем примере последовательность де Брейна используется для определения индекса наименее значимого бита набора (эквивалентно подсчету количества конечных нулевых битов) в 32-битном беззнаковом целом числе:
uint8_t lowerBitIndex ( uint32_t v ) { static const uint8_t BitPositionLookup [ 32 ] = // хэш-таблица { 0 , 1 , 28 , 2 , 29 , 14 , 24 , 3 , 30 , 22 , 20 , 15 , 25 , 17 , 4 , 8 , 31 , 27 , 13 , 23 , 21 , 19 , 16 , 7 , 26 , 12 , 18 , 6 , 11 , 5 , 10 , 9 }; вернуть BitPositionLookup [(( uint32_t )(( v & - v ) * 0x077CB531U )) >> 27 ]; } Функция lowestBitIndex()возвращает индекс наименее значимого установленного бита в v или ноль, если v не имеет установленных битов. Константа 0x077CB531U в выражении — это последовательность B (2, 5) 0000 0111 0111 1100 1011 0101 0011 0001 (пробелы добавлены для ясности). Операция (v & -v)обнуляет все биты, кроме набора наименее значимых битов, в результате чего получается новое значение, являющееся степенью числа 2. Эта степень числа 2 умножается (арифметическое по модулю 2 32 ) на последовательность де Брейна, в результате чего получается 32-битное произведение, в котором последовательность бит из 5 старших битов уникальна для каждой степени числа 2. 5 старших битов сдвигаются в позиции младших битов для получения хэш-кода в диапазоне [0, 31], который затем используется в качестве индекса в хэш-таблице BitPositionLookup. Выбранное значение хэш-таблицы является индексом бита наименее значимых битов в v .
В следующем примере определяется индекс самого старшего бита в 32-битном беззнаковом целом числе:
uint32_t keepHighestBit ( uint32_t n ) { n |= ( n >> 1 ); n |= ( n >> 2 ) ; n |= ( n >> 4 ); n |= ( n >> 8 ); n |= ( n >> 16 ); return n - ( n >> 1 ); } uint8_t highestBitIndex ( uint32_t v ) { static const uint8_t BitPositionLookup [ 32 ] = { // хэш-таблица 0 , 1 , 16 , 2 , 29 , 17 , 3 , 22 , 30 , 20 , 18 , 11 , 13 , 4 , 7 , 23 , 31 , 15 , 28 , 21 , 19 , 10 , 12 , 6 , 14 , 27 , 9 , 5 , 26 , 8 , 25 , 24 , }; вернуть BitPositionLookup [( keepHighestBit ( v ) * 0x06EB14F9U ) >> 27 ]; } В приведенном выше примере используется альтернативная последовательность де Брейна (0x06EB14F9U) с соответствующим переупорядочением значений массива. Выбор этой конкретной последовательности де Брейна произволен, но значения хэш-таблицы должны быть упорядочены так, чтобы соответствовать выбранной последовательности де Брейна. Функция keepHighestBit()обнуляет все биты, кроме самого старшего бита набора, в результате чего получается значение, являющееся степенью числа 2, которое затем обрабатывается так же, как в предыдущем примере.
Атаки на замки методом грубой силы

| B{10,3} с цифрами, читаемыми сверху вниз, затем слева направо; [15] добавление «00» дает строку для подбора трехзначного кодового замка | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 001 | |||||||||
| 002 | |||||||||
| 003 | |||||||||
| 004 | |||||||||
| 005 | |||||||||
| 006 | |||||||||
| 007 | |||||||||
| 008 | |||||||||
| 009 | |||||||||
| 011 | |||||||||
| 012 | 112 | ||||||||
| 013 | 113 | ||||||||
| 014 | 114 | ||||||||
| 015 | 115 | ||||||||
| 016 | 116 | ||||||||
| 017 | 117 | ||||||||
| 018 | 118 | ||||||||
| 019 | 119 | ||||||||
| 021 | |||||||||
| 022 | 122 | ||||||||
| 023 | 123 | 223 | |||||||
| 024 | 124 | 224 | |||||||
| 025 | 125 | 225 | |||||||
| 026 | 126 | 226 | |||||||
| 027 | 127 | 227 | |||||||
| 028 | 128 | 228 | |||||||
| 029 | 129 | 229 | |||||||
| 031 | |||||||||
| 032 | 132 | ||||||||
| 033 | 133 | 233 | |||||||
| 034 | 134 | 234 | 334 | ||||||
| 035 | 135 | 235 | 335 | ||||||
| 036 | 136 | 236 | 336 | ||||||
| 037 | 137 | 237 | 337 | ||||||
| 038 | 138 | 238 | 338 | ||||||
| 039 | 139 | 239 | 339 | ||||||
| 041 | |||||||||
| 042 | 142 | ||||||||
| 043 | 143 | 243 | |||||||
| 044 | 144 | 244 | 344 | ||||||
| 045 | 145 | 245 | 345 | 445 | |||||
| 046 | 146 | 246 | 346 | 446 | |||||
| 047 | 147 | 247 | 347 | 447 | |||||
| 048 | 148 | 248 | 348 | 448 | |||||
| 049 | 149 | 249 | 349 | 449 | |||||
| 051 | |||||||||
| 052 | 152 | ||||||||
| 053 | 153 | 253 | |||||||
| 054 | 154 | 254 | 354 | ||||||
| 055 | 155 | 255 | 355 | 455 | |||||
| 056 | 156 | 256 | 356 | 456 | 556 | ||||
| 057 | 157 | 257 | 357 | 457 | 557 | ||||
| 058 | 158 | 258 | 358 | 458 | 558 | ||||
| 059 | 159 | 259 | 359 | 459 | 559 | ||||
| 061 | |||||||||
| 062 | 162 | ||||||||
| 063 | 163 | 263 | |||||||
| 064 | 164 | 264 | 364 | ||||||
| 065 | 165 | 265 | 365 | 465 | |||||
| 066 | 166 | 266 | 366 | 466 | 566 | ||||
| 067 | 167 | 267 | 367 | 467 | 567 | 667 | |||
| 068 | 168 | 268 | 368 | 468 | 568 | 668 | |||
| 069 | 169 | 269 | 369 | 469 | 569 | 669 | |||
| 071 | |||||||||
| 072 | 172 | ||||||||
| 073 | 173 | 273 | |||||||
| 074 | 174 | 274 | 374 | ||||||
| 075 | 175 | 275 | 375 | 475 | |||||
| 076 | 176 | 276 | 376 | 476 | 576 | ||||
| 077 | 177 | 277 | 377 | 477 | 577 | 677 | |||
| 078 | 178 | 278 | 378 | 478 | 578 | 678 | 778 | ||
| 079 | 179 | 279 | 379 | 479 | 579 | 679 | 779 | ||
| 081 | |||||||||
| 082 | 182 | ||||||||
| 083 | 183 | 283 | |||||||
| 084 | 184 | 284 | 384 | ||||||
| 085 | 185 | 285 | 385 | 485 | |||||
| 086 | 186 | 286 | 386 | 486 | 586 | ||||
| 087 | 187 | 287 | 387 | 487 | 587 | 687 | |||
| 088 | 188 | 288 | 388 | 488 | 588 | 688 | 788 | ||
| 089 | 189 | 289 | 389 | 489 | 589 | 689 | 789 | 889 | |
| 091 | |||||||||
| 092 | 192 | ||||||||
| 093 | 193 | 293 | |||||||
| 094 | 194 | 294 | 394 | ||||||
| 095 | 195 | 295 | 395 | 495 | |||||
| 096 | 196 | 296 | 396 | 496 | 596 | ||||
| 097 | 197 | 297 | 397 | 497 | 597 | 697 | |||
| 098 | 198 | 298 | 398 | 498 | 598 | 698 | 798 | ||
| 099 | 199 | 299 | 399 | 499 | 599 | 699 | 799 | 899 | (00) |
Последовательность де Брейна может быть использована для сокращения атаки методом перебора на кодовый замок типа PIN , который не имеет клавиши «ввод» и принимает последние n введенных цифр. Например, цифровой дверной замок с 4-значным кодом (каждая цифра имеет 10 возможностей от 0 до 9) будет иметь B (10, 4) решений с длиной10 000. Поэтому, только самое большее10 000 + 3 =Для открытия замка необходимо 10 003 (так как решения циклические) нажатия, тогда как для перебора всех кодов по отдельности потребуется 4 ×10 000 =40 000 нажатий.

Камера распознает матрицу 6×6 точек, каждая из которых смещена относительно синей сетки (не напечатана) в одном из 4 направлений.
Комбинации относительных смещений 6-битной последовательности де Брейна между столбцами и между строками дают ее абсолютное положение на цифровой бумаге.
f-кратные последовательности де Брейна
F -кратная n-арная последовательность де Брейна является расширением понятия n -арной последовательности де Брейна, таким образом, что последовательность длины содержит каждую возможную подпоследовательность длины n ровно f раз. Например, для циклических последовательностей 11100010 и 11101000 являются двукратными бинарными последовательностями де Брейна. Число двукратных последовательностей де Брейна для равно , другие известные числа [16] равны , , и .
тор де Брейна
Тор де Брейна — это тороидальный массив, обладающий тем свойством, что каждая k -ичная матрица размера m на n встречается ровно один раз.
Такой шаблон может быть использован для двумерного позиционного кодирования способом, аналогичным описанному выше для вращательного кодирования. Положение может быть определено путем изучения матрицы m -by -n, непосредственно прилегающей к датчику, и вычисления ее положения на торе де Брейна.
декодирование де Брейна
Вычисление положения конкретного уникального кортежа или матрицы в последовательности де Брейна или торе известно как проблема декодирования де Брейна . Эффективные алгоритмы декодирования существуют для специальных, рекурсивно построенных последовательностей [17] и распространяются на двумерный случай. [18] Декодирование де Брейна представляет интерес, например, в случаях, когда большие последовательности или торы используются для позиционного кодирования.
Смотрите также
- Нормальное число
- Регистр сдвига с линейной обратной связью
- n -последовательность
- ЛУЧШАЯ теорема
- Суперперестановка
Примечания
- ^ де Брейн (1946).
- ^ abc de Bruijn (1975).
- ^ Браун (1869); Стайн (1963); Как (2000); Кнут (2006); Холл (2008).
- ^ Поппер (2002).
- ^ Кляйн (2013).
- ^ По данным Берстеля и Перрена (2007), последовательность, сгенерированная таким образом, была впервые описана (с другим методом генерации) Мартином (1934), а связь между ней и словами Линдона была обнаружена Фредриксеном и Майораной (1978).
- ^ ab Хиггинс (2012).
- ^ Горески и Клэппер (2012).
- ^ Ралстон (1982), стр. 136–139.
- ^ "Последовательности Де Брейна" . Мудрец . Проверено 7 марта 2023 г.
- ^ Агирре, Маттар и Магис-Вайнберг (2011).
- ^ "генератор цикла де Брейна". Архивировано из оригинала 2016-01-26 . Получено 2015-09-15 .
- ^ Ван Линт и Уилсон (2001).
- ^ Андерсон (1997–2009); Буш (2009)
- ^ «Последовательность де Брейна (ДеБрюйна) (K = 10, n = 3)» .
- ^ Осипов (2016).
- ^ Тулиани (2001).
- ^ Херлберт и Айзек (1993).
Ссылки
- ван Аарденне-Эренфест, Таня ; де Брейн, Николаас Говерт (1951). «Схемы и деревья в ориентированных линейных графах» (PDF) . Саймон Стевин . 28 : 203–217 . МР 0047311.
- Aguirre, GK; Mattar, MG; Magis-Weinberg, L. (2011). "циклы де Брейна для нейронного декодирования". NeuroImage . 56 (3): 1293– 1300. doi :10.1016/j.neuroimage.2011.02.005. PMC 3104402 . PMID 21315160. Архивировано из оригинала 2016-01-26 . Получено 2015-06-04 .
- Андерсон, Шон Эрон (1997–2009). «Bit Twiddling Hacks». Стэнфордский университет . Получено 12 февраля 2009 г.
- Берстель, Жан ; Перрен, Доминик (2007). «Истоки комбинаторики слов» (PDF) . Европейский журнал комбинаторики . 28 (3): 996– 1022. doi :10.1016/j.ejc.2005.07.019. MR 2300777.
- Браун, К. П. (1869). Объяснение санскритской просодии и числовых символов. стр. 28.
- де Брейн, Николаас Говерт (1946). «Комбинаторная задача» (PDF) . Учеб. Koninklijke Nederlandse Akademie V. Wetenschappen . 49 : 758–764 . MR 0018142, Indagationes Mathematicae 8 : 461–467.
{{cite journal}}: CS1 maint: постскриптум ( ссылка ) - де Брюйн, Николас Говерт (1975). Признание приоритета C. Flye Sainte-Marie по подсчету круговых расположений из 2n нулей и единиц, которые показывают каждое n-буквенное слово ровно один раз (PDF) . TH-Report 75-WSK-06. Технологический университет Эйндховена.
- Буш, Филип (2009). "Computing Trailing Zeros HOWTO". Архивировано из оригинала 29-01-2015 . Получено 29-01-2015 .
- Флай Сент-Мари, Камилла (1894). «Решение вопроса № 48». L'Intermediaire des Mathématiciens . 1 : 107–110 .
- Горески, Марк ; Клаппер, Эндрю (2012). "8.2.5 Генерация сдвиговых регистров последовательностей де Брейна". Алгебраические сдвиговые регистровые последовательности. Cambridge University Press . С. 174– 175. ISBN 978-1-10701499-2.
- Холл, Рэйчел В. (2008). «Математика для поэтов и барабанщиков» (PDF) . Math Horizons . 15 (3): 10– 11. doi :10.1080/10724117.2008.11974752. S2CID 3637061. Архивировано из оригинала (PDF) 2012-02-12 . Получено 2008-10-22 .
- Хиггинс, Питер (ноябрь 2012 г.). "Преобразования Берроуза-Уиллера и слова де Брейна" (PDF) . Получено 11.02.2017 .
- Hurlbert, Glenn; Isaak, Garth (1993). «О проблеме тора де Брейна». Журнал комбинаторной теории . Серия A. 64 (1): 50– 62. doi : 10.1016/0097-3165(93)90087-O . MR 1239511.
- Как, Субхаш (2000). «Яматараджабханасалагам — интересная комбинаторная сутра» (PDF) . Индийский журнал истории науки . 35 (2): 123– 127. Архивировано из оригинала (PDF) 29 октября 2014 г.
- Кляйн, Андреас (2013). Потоковые шифры. Springer. стр. 59. ISBN 978-1-44715079-4.
- Кнут, Дональд Эрвин (2006). Искусство программирования, выпуск 4: Генерация всех деревьев – История комбинаторной генерации. Эддисон–Уэсли . стр. 50. ISBN 978-0-321-33570-8.
- Фредриксен, Гарольд; Майорана, Джеймс (1978). «Ожерелья из бусин k цветов и k-арные последовательности де Брейна». Дискретная математика . 23 (3): 207– 210. doi : 10.1016/0012-365X(78)90002-X . MR 0523071.
- Мартин, Монро Х. (1934). "Проблема в расположениях" (PDF) . Бюллетень Американского математического общества . 40 (12): 859– 864. doi : 10.1090/S0002-9904-1934-05988-3 . MR 1562989.
- Осипов, Владимир (2016). «Вейвлет-анализ символических последовательностей и двукратных последовательностей де Брейна». Журнал статистической физики . 164 (1): 142– 165. arXiv : 1601.02097 . Bibcode : 2016JSP...164..142O. doi : 10.1007/s10955-016-1537-5. ISSN 1572-9613. S2CID 16535836.
- Поппер, Карл (2002) [1934]. Логика научного открытия. Routledge. стр. 294. ISBN 978-0-415-27843-0.
- Ралстон, Энтони (1982). «Последовательности де Брейна — модельный пример взаимодействия дискретной математики и компьютерной науки». Mathematics Magazine . 55 (3): 131– 143. doi :10.2307/2690079. JSTOR 2690079. MR 0653429.
- Стайн, Шерман К. (1963). «Яматараджабханасалагам». Вселенная, созданная человеком: Введение в дух математики . С. 110–118 .Перепечатано в Wardhaugh, Benjamin, ed. (2012), Богатство чисел: Антология 500 лет популярных математических трудов , Princeton University Press , стр. 139–144.
- Тулиани, Джонатан (2001). "Последовательности де Брейна с эффективными алгоритмами декодирования". Дискретная математика . 226 ( 1– 3): 313– 336. doi :10.1016/S0012-365X(00)00117-5. MR 1802599.
- ван Линт, Дж. Х .; Уилсон, Ричард Майкл (2001). Курс комбинаторики. Cambridge University Press . стр. 71. ISBN 978-0-52100601-9.
Внешние ссылки
- Вайсштейн, Эрик В. «Последовательность де Брёйна». Математический мир .
- Последовательность OEIS A166315 (лексикографически наименьшие двоичные последовательности де Брейна)
- Последовательность Де Брейна
- CGI-генератор
- Генератор апплетов
- Генератор и декодер Javascript. Реализация алгоритма Дж. Тулиани.
- Дверной кодовый замок
- Минимальные массивы, содержащие все подмассивные комбинации символов: последовательности де Брейна и торы
- http://debruijnsequence.org содержит множество типов последовательностей де Брейна.














