Циклы, связанные кубом

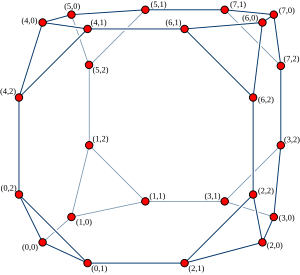
В теории графов кубически -связанные циклы — это неориентированный кубический граф , образованный заменой каждой вершины гиперкубического графа циклом . Он был введен Препаратой и Вюйемином (1981) для использования в качестве сетевой топологии в параллельных вычислениях .

Кубически-связанные циклы порядка n (обозначаемые CCC _n ) можно определить как граф, образованный из набора n 2 ⁿ узлов, индексированных парами чисел ( x , y ), где 0 ≤ x < 2 ⁿ и 0 ≤ y < n . Каждый такой узел соединен с тремя соседями: ( x , ( y + 1) mod n ) , ( x , ( y − 1) mod n ) и ( x ⊕ 2 ^y , y ) , где «⊕» обозначает побитовую операцию исключающего или над двоичными числами.

Этот граф также можно интерпретировать как результат замены каждой вершины n -мерного гиперкубического графа на n -вершинный цикл. Вершины гиперкубического графа индексируются числами x , а позиции внутри каждого цикла - числами y .

Связанные кубом циклы порядка n — это граф Кэли группы , действующий на двоичные слова длины n путем вращения и переворачивания битов слова. ^{[1] Генераторы, используемые для формирования этого графа Кэли из} группы , — это элементы группы, которые действуют путем вращения слова на одну позицию влево, вращения его на одну позицию вправо или переворачивания его первого бита. Поскольку это граф Кэли, он является вершинно-транзитивным : существует симметрия графа, отображающая любую вершину в любую другую вершину.

Диаметр кубически связанных циклов порядка n равен 2 n + ⌊n/2⌋ − 2 для любого n ≥ 4; самая дальняя точка от ( x ,  y ) равна (2 ⁿ  −  x  − 1, ( y  +  n /2) mod  n ). ^[2] Сикора и Врто (1993) показали, что число пересечений CCC _n равно ((1/20) + o(1)) 4 ⁿ .

Согласно гипотезе Ловаса , граф кубически связных циклов всегда должен содержать гамильтонов цикл , и теперь известно, что это правда. В более общем смысле, хотя эти графы не являются панциклическими , они содержат циклы всех, кроме ограниченного числа возможных четных длин, а когда n нечетно, они также содержат многие из возможных нечетных длин циклов. ^[3]

Кубически-связанные циклы были исследованы Preparata & Vuillemin (1981), которые применили эти графы в качестве схемы взаимосвязей сети, соединяющей процессоры в параллельном компьютере . В этом приложении кубически-связанные циклы обладают преимуществами связности гиперкубов, при этом требуя только трех соединений на процессор. Preparata и Vuillemin показали, что планарная компоновка, основанная на этой сети, имеет оптимальную сложность площадь × время ² для многих задач параллельной обработки.

• Акерс, Шелдон Б.; Кришнамурти, Балакришнан (1989), «Групповая теоретико-модель для симметричных сетей взаимосвязей», IEEE Transactions on Computers , 38 (4): 555–566, doi :10.1109/12.21148.
• Аннекстайн, Фред; Баумслаг, Марк; Розенберг, Арнольд Л. (1990), «Графы групповых действий и параллельные архитектуры», SIAM Journal on Computing , 19 (3): 544–569, doi :10.1137/0219037.
• Фриш, Иван; Гавел, Иван; Либль, Петр (1997), «Диаметр кубически-связанных циклов», Information Processing Letters , 61 (3): 157–160, doi :10.1016/S0020-0190(97)00013-6.
• Germa, Anne; Heydemann, Marie-Claude; Sotteau, Dominique (1998), «Циклы в графе кубически связанных циклов», Discrete Applied Mathematics , 83 (1–3): 135–155, doi : 10.1016/S0166-218X(98)80001-2 , MR  1622968.
• Препарата, Франко П.; Вюйемен , Жан (1981), «Кубически связанные циклы: универсальная сеть для параллельных вычислений», Communications of the ACM , 24 (5): 300–309, doi : 10.1145/358645.358660, hdl : 2142/74219 , S2CID  8538576.
• Sýkora, Ondrej; Vrťo, Imrich (1993), "О числах пересечений гиперкубов и кубических связанных циклов", BIT Numerical Mathematics , 33 (2): 232–237, doi :10.1007/BF01989746, hdl : 11858/00-001M-0000-002D-92E4-9 , S2CID  15913153.