Непрерывное распределение Бернулли
Распределение вероятностей
Непрерывное распределение Бернулли
Функция плотности вероятности
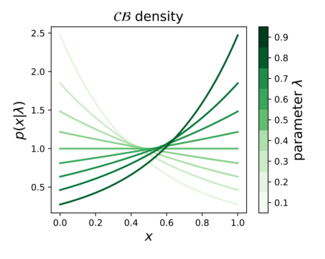Функция плотности вероятности непрерывного распределения Бернулли
Обозначение С Б ( λ ) {\displaystyle {\mathcal {CB}}(\lambda )}
Параметры λ ∈ ( 0 , 1 ) {\displaystyle \лямбда \in (0,1)}
Поддерживать х ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]}
PDF С ( λ ) λ х ( 1 − λ ) 1 − х {\displaystyle C(\lambda )\lambda ^{x}(1-\lambda )^{1-x}\!}
где С ( λ ) = { 2 если  λ = 1 2 2 танг − 1 ⁡ ( 1 − 2 λ ) 1 − 2 λ  в противном случае {\displaystyle C(\lambda )={\begin{cases}2&{\text{if }}\lambda ={\frac {1}{2}}\\{\frac {2\tanh ^{-1}(1-2\lambda )}{1-2\lambda }}&{\text{ otherwise}}\end{cases}}}
СДФ { х  если  λ = 1 2 λ х ( 1 − λ ) 1 − х + λ − 1 2 λ − 1  в противном случае {\displaystyle {\begin{cases}x&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda ^{x}(1-\lambda )^{1-x}+\lambda -1}{2\lambda -1}}&{\text{ otherwise}}\end{cases}}\!}
Иметь в виду Э ⁡ [ Х ] = { 1 2  если  λ = 1 2 λ 2 λ − 1 + 1 2 танг − 1 ⁡ ( 1 − 2 λ )  в противном случае {\displaystyle \operatorname {E} [X]={\begin{cases}{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+{\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ otherwise}}\end{cases}}\!}
Дисперсия вар ⁡ [ Х ] = { 1 12  если  λ = 1 2 − ( 1 − λ ) λ ( 1 − 2 λ ) 2 + 1 ( 2 танг − 1 ⁡ ( 1 − 2 λ ) ) 2  в противном случае {\displaystyle \operatorname {var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\-{\frac {(1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2}}}&{\text{ otherwise}}\end{cases}}\!}

В теории вероятностей , статистике и машинном обучении непрерывное распределение Бернулли [1] [2] [3] представляет собой семейство непрерывных распределений вероятностей, параметризованных одним параметром формы , определенным на единичном интервале , как: λ ∈ ( 0 , 1 ) {\displaystyle \лямбда \in (0,1)} х ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]}

п ( х | λ ) ∝ λ х ( 1 − λ ) 1 − х . {\displaystyle p(x|\lambda )\propto \lambda ^{x}(1-\lambda )^{1-x}.}

Непрерывное распределение Бернулли возникает в глубоком обучении и компьютерном зрении , в частности, в контексте вариационных автокодировщиков , [4] [5] для моделирования интенсивности пикселей естественных изображений. Как таковое, оно определяет надлежащий вероятностный аналог для обычно используемой двоичной кросс-энтропийной потери, которая часто применяется к непрерывным, -значным данным. [6] [7] [8] [9] Такая практика равносильна игнорированию нормализующей константы непрерывного распределения Бернулли, поскольку двоичная кросс-энтропийная потеря определяет только истинное логарифмическое правдоподобие для дискретных, -значных данных. [ 0 , 1 ] {\displaystyle [0,1]} { 0 , 1 } {\displaystyle \{0,1\}}

Непрерывный Бернулли также определяет экспоненциальное семейство распределений. Записывая для натурального параметра , плотность можно переписать в канонической форме: . η = log ⁡ ( λ / ( 1 − λ ) ) {\displaystyle \eta =\log \left(\lambda /(1-\lambda )\right)} p ( x | η ) ∝ exp ⁡ ( η x ) {\displaystyle p(x|\eta )\propto \exp(\eta x)}

Статистический вывод

При наличии выборки точек с , оценка максимального правдоподобия представляет собой эмпирическое среднее , N {\displaystyle N} x 1 , … , x n {\displaystyle x_{1},\dots ,x_{n}} x i ∈ [ 0 , 1 ] ∀ i {\displaystyle x_{i}\in [0,1]\,\forall i} λ {\displaystyle \lambda }

λ ^ = x ¯ = 1 N ∑ i = 1 n x i . {\displaystyle {\hat {\lambda }}={\bar {x}}={\frac {1}{N}}\sum _{i=1}^{n}x_{i}.}

Эквивалентно, оценка для натурального параметра — это логарифм , η {\displaystyle \eta } x ¯ {\displaystyle {\bar {x}}}

η ^ = logit ( x ¯ ) = log ⁡ ( x ¯ / ( 1 − x ¯ ) ) . {\displaystyle {\hat {\eta }}={\text{logit}}({\bar {x}})=\log({\bar {x}}/(1-{\bar {x}})).}

Распределение Бернулли

Непрерывное распределение Бернулли можно рассматривать как непрерывную релаксацию распределения Бернулли , которое определяется на дискретном множестве функцией массы вероятности : { 0 , 1 } {\displaystyle \{0,1\}}

p ( x ) = p x ( 1 − p ) 1 − x , {\displaystyle p(x)=p^{x}(1-p)^{1-x},}

где — скалярный параметр между 0 и 1. Применение этой же функциональной формы к непрерывному интервалу приводит к непрерывной функции плотности вероятности Бернулли с точностью до нормировочной константы. p {\displaystyle p} [ 0 , 1 ] {\displaystyle [0,1]}

Бета-распределение

Бета -распределение имеет функцию плотности:

p ( x ) ∝ x α − 1 ( 1 − x ) β − 1 , {\displaystyle p(x)\propto x^{\alpha -1}(1-x)^{\beta -1},}

что можно переписать как:

p ( x ) ∝ x 1 α 1 − 1 x 2 α 2 − 1 , {\displaystyle p(x)\propto x_{1}^{\alpha _{1}-1}x_{2}^{\alpha _{2}-1},}

где - положительные скалярные параметры, а представляет собой произвольную точку внутри 1- симплекса , . Меняя роли параметра и аргумента в этой функции плотности, получаем: α 1 , α 2 {\displaystyle \alpha _{1},\alpha _{2}} ( x 1 , x 2 ) {\displaystyle (x_{1},x_{2})} Δ 1 = { ( x 1 , x 2 ) : x 1 > 0 , x 2 > 0 , x 1 + x 2 = 1 } {\displaystyle \Delta ^{1}=\{(x_{1},x_{2}):x_{1}>0,x_{2}>0,x_{1}+x_{2}=1\}}

p ( x ) ∝ α 1 x 1 α 2 x 2 . {\displaystyle p(x)\propto \alpha _{1}^{x_{1}}\alpha _{2}^{x_{2}}.}

Это семейство идентифицируемо только с точностью до линейного ограничения , откуда получаем: α 1 + α 2 = 1 {\displaystyle \alpha _{1}+\alpha _{2}=1}

p ( x ) ∝ λ x 1 ( 1 − λ ) x 2 , {\displaystyle p(x)\propto \lambda ^{x_{1}}(1-\lambda )^{x_{2}},}

что в точности соответствует непрерывной плотности Бернулли.

Экспоненциальное распределение

Экспоненциальное распределение, ограниченное единичным интервалом, эквивалентно непрерывному распределению Бернулли с соответствующим [ каким? ] параметром.

Непрерывное категориальное распределение

Многомерное обобщение непрерывного Бернулли называется непрерывно-категоричным. [10]

Ссылки

  1. ^ Лоаиза-Ганем, Г. и Каннингем, Дж. П. (2019). Непрерывный Бернулли: исправление распространенной ошибки в вариационных автоэнкодерах. В Advances in Neural Information Processing Systems (стр. 13266-13276).
  2. ^ Дистрибутивы PyTorch. https://pytorch.org/docs/stable/distributions.html#continuousbernoulli
  3. ^ Tensorflow Probability. https://www.tensorflow.org/probability/api_docs/python/tfp/edward2/ContinuousBernoulli Архивировано 25 ноября 2020 г. на Wayback Machine
  4. ^ Кингма, Д. П. и Веллинг, М. (2013). Автоматическое кодирование вариационного байеса. Препринт arXiv arXiv:1312.6114.
  5. ^ Кингма, Д.П. и Веллинг, М. (2014, апрель). Стохастический градиент VB и вариационный автокодировщик. На Второй международной конференции по представлениям обучения, ICLR (т. 19).
  6. ^ Larsen, ABL, Sønderby, SK, Larochelle, H., & Winther, O. (2016, июнь). Автокодирование за пределами пикселей с использованием метрики выученного сходства. На Международной конференции по машинному обучению (стр. 1558-1566).
  7. ^ Цзян, З., Чжэн, И., Тан, Х., Тан, Б. и Чжоу, Х. (2017, август). Вариационное глубокое встраивание: неконтролируемый и генеративный подход к кластеризации. В трудах 26-й Международной совместной конференции по искусственному интеллекту (стр. 1965-1972).
  8. ^ Учебное пособие по PyTorch VAE: https://github.com/pytorch/examples/tree/master/vae.
  9. ^ Учебное пособие по Keras VAE: https://blog.keras.io/building-autoencoders-in-keras.html.
  10. ^ Гордон-Родригес, Э., Лоаиза-Ганем, Г. и Каннингем, Дж. П. (2020). Непрерывная категориальная: новое симплексно-значное экспоненциальное семейство. На 36-й Международной конференции по машинному обучению, ICML 2020. Международное общество машинного обучения (IMLS).
Retrieved from "https://en.wikipedia.org/w/index.php?title=Continuous_Bernoulli_distribution&oldid=1251470393"