Изучение положений, основанных на конфликтах

В информатике обучение на основе конфликта ( CDCL ) — это алгоритм решения проблемы выполнимости булевых уравнений (SAT). При наличии булевой формулы задача SAT требует назначения переменных таким образом, чтобы вся формула была оценена как истинная. Внутренние механизмы решателей CDCL SAT были вдохновлены решателями DPLL . Главное различие между CDCL и DPLL заключается в том, что обратный переход CDCL не является хронологическим.

Обучение предложениям, основанное на конфликтах, было предложено Маркесом-Сильвой и Каремом А. Сакаллахом (1996, 1999) ^{[1] [2]} и Байардо и Шрагом (1997). ^[3]

Проблема выполнимости состоит в нахождении удовлетворяющего задания для заданной формулы в конъюнктивной нормальной форме (КНФ).

Пример такой формулы:

( ( не А ) или (не С ))   и   ( В или С ),

или, используя общепринятую запись: ^[4]

${\displaystyle (\lnot A\or \lnot C)\land (B\or C)}$

где A , B , C — логические переменные, , , и — литералы, а и — предложения.${\displaystyle \lnot A}$${\displaystyle \lnot C}$${\displaystyle Б}$${\displaystyle С}$${\displaystyle \lnot A\or \lnot C}$${\displaystyle B\или C}$

Удовлетворительное задание для этой формулы, например:

${\ displaystyle A = \ mathrm {False}, B = \ mathrm {False}, C = \ mathrm {True} }$

поскольку это делает истинным как первое предложение (поскольку истинно), так и второе (поскольку истинно).${\displaystyle \lnot A}$${\displaystyle С}$

В этом примере используются три переменные ( A , B , C ), и для каждой из них есть два возможных назначения (True и False). Таким образом, у вас есть возможности. В этом небольшом примере можно использовать поиск методом перебора , чтобы перебрать все возможные назначения и проверить, удовлетворяют ли они формуле. Но в реальных приложениях с миллионами переменных и предложений поиск методом перебора непрактичен. Ответственность решателя SAT заключается в эффективном и быстром поиске удовлетворяющего назначения путем применения различных эвристик для сложных формул CNF.${\displaystyle 2^{3}=8}$

Если в предложении все литералы или переменные, кроме одного, оценены как False, то свободный литерал должен быть True, чтобы предложение было True. Например, если нижеприведенное неудовлетворенное предложение оценивается с помощью и мы должны иметь , чтобы предложение было true.${\displaystyle A=\mathrm {False} }$${\displaystyle B=\mathrm {False} }$${\displaystyle C=\mathrm {Истина} }$${\displaystyle (А\лор Б\лор С)}$

Повторное применение правила предложения единицы называется распространением единицы или распространением булевых ограничений (BCP).

Рассмотрим два предложения и . Предложение , полученное путем слияния двух предложений и удаления обоих и , называется резольвентой двух предложений.${\displaystyle (А\лор Б\лор С)}$${\displaystyle (\neg C\lor D\lor \neg E)}$${\displaystyle (A\lor B\lor D\lor \neg E)}$${\displaystyle \отрицательный С}$${\displaystyle С}$

В этом разделе не указаны источники . Пожалуйста, помогите улучшить этот раздел , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены . ( Июль 2024 г. ) ( Узнайте, как и когда удалять это сообщение )

Этот раздел нуждается в расширении . Вы можете помочь, дополнив его. ( Июль 2024 )

Обучение предложениям, основанным на конфликтах, работает следующим образом.

1. Выберите переменную и назначьте True или False. Это называется состоянием решения. Запомните назначение.
2. Применить распространение булевых ограничений (единичное распространение).
3. Постройте график импликации .
4. Если есть какой-либо конфликт
   1. Найдите разрез в графе импликации, который привел к конфликту.
   2. Выведите новое предложение, которое является отрицанием присваиваний, которые привели к конфликту.
   3. Нехронологически вернуться («вернуться») на соответствующий уровень принятия решения, где была назначена первая переменная, вовлеченная в конфликт
5. В противном случае продолжайте с шага 1, пока не будут назначены все значения переменных.

Наглядный пример алгоритма CDCL: ^[4]

• 
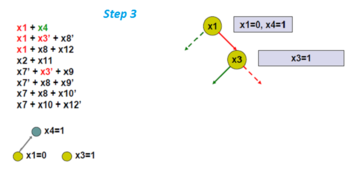
  Сначала выбираем переменную ветвления, а именно x1 . Желтый круг означает произвольное решение.
• 
  Теперь применим единичное распространение, которое дает, что x4 должно быть 1 (т.е. True). Серый кружок означает принудительное назначение переменной во время единичного распространения. Полученный график называется импликационным графиком .
• 
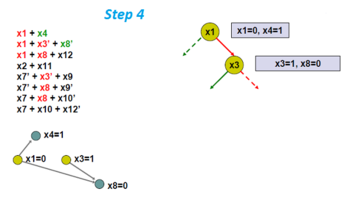
  Произвольно выберите другую переменную ветвления, x3 .
• 
  Примените единичное распространение и найдите новый граф импликации.
• 
  Здесь переменные x8 и x12 принудительно устанавливаются равными 0 и 1 соответственно.
• 
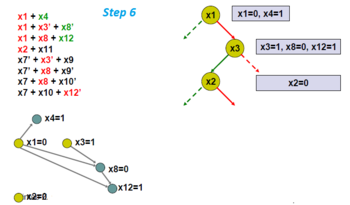
  Выберите другую переменную ветвления, x2 .
• 
  Найдите граф импликации.
• 
  Выберите другую переменную ветвления, x7 .
• 
  Найдите граф импликации.
• 
  Найден конфликт!
• 
  Найдите разрез, который привел к этому конфликту. Из разреза найдите конфликтующее условие.
• 
  Возьмите отрицание этого условия и сделайте его предложением.
• 
  Добавьте к проблеме оговорку о конфликте положений.
• 
  Нехронологический обратный переход на соответствующий уровень принятия решения, который в данном случае является вторым по величине уровнем принятия решения литералов в изученном предложении.
• 
  Вернитесь назад и установите соответствующие значения переменных.

DPLL — это надежный и полный алгоритм для SAT. Решатели CDCL SAT реализуют DPLL, но могут изучать новые предложения и возвращаться нехронологически. Изучение предложений с анализом конфликта не влияет ни на обоснованность, ни на полноту. Анализ конфликта идентифицирует новые предложения с помощью операции разрешения. Следовательно, каждое изученное предложение может быть выведено из исходных предложений и других изученных предложений с помощью последовательности шагов разрешения. Если cN — это новое изученное предложение, то ϕ выполнимо тогда и только тогда, когда ϕ ∪ {cN} также выполнимо. Более того, измененный шаг возврата также не влияет на обоснованность или полноту, поскольку информация возврата получается из каждого нового изученного предложения. ^[5]

Основное применение алгоритма CDCL — в различных решателях SAT, включая:

• МиниСАТ
• Zchaff SAT
• Z3
• Глюкоза ^[6]
• ManySAT и т.д.

Алгоритм CDCL сделал решатели SAT настолько мощными, что они эффективно используются в нескольких ^{[ требуется ссылка ]} областях реального мира, таких как планирование ИИ, биоинформатика, генерация тестовых шаблонов программного обеспечения, зависимости пакетов программного обеспечения, проверка моделей оборудования и программного обеспечения и криптография.

Связанные с CDCL алгоритмы — это алгоритм Дэвиса–Патнэма и алгоритм DPLL . Алгоритм DP использует опровержение резолюции и имеет потенциальную проблему доступа к памяти. ^{[ необходима цитата ]} В то время как алгоритм DPLL подходит для случайно сгенерированных экземпляров, он плох для экземпляров, сгенерированных в практических приложениях. CDCL — более мощный подход к решению таких проблем, поскольку применение CDCL обеспечивает меньший поиск в пространстве состояний по сравнению с DPLL.

• 
  DPLL: без обучения и хронологического возврата.
• 
  CDCL: изучение предложений, основанное на конфликтах, и нехронологический возврат.

• Мартин Дэвис; Хилари Патнэм (1960). «Вычислительная процедура для теории квантификации». J. ACM . 7 (3): 201– 215. doi : 10.1145/321033.321034 . S2CID  31888376.
• Мартин Дэвис; Джордж Логеманн; Дональд Лавленд (июль 1962 г.). «Машинная программа для доказательства теорем». Сообщения ACM . 5 (7): 394– 397. doi :10.1145/368273.368557. hdl : 2027/mdp.39015095248095 . S2CID  15866917.
• Мэтью В. Москевич; Конор Ф. Мэдиган; Ин Чжао; Линтао Чжан; Шарад Малик (2001). «Чафф: разработка эффективного решателя SAT» (PDF) . Труды 38-й ежегодной конференции по автоматизации проектирования (DAC) . стр.  530–535 .
• Lintao Zhang; Conor F. Madigan; Matthew H. Moskewicz; Sharad Malik (2001). "Эффективное обучение, управляемое конфликтами, в решателе булевой выполнимости" (PDF) . Proc. IEEE/ACM Int. Conf. on Computer-aided design (ICCAD) . pp.  279–285 .
• Презентация – «Решение SAT: от Дэвиса-Патнэма до Зчаффа и далее» Линьтао Чжана. (Несколько фотографий взяты из его презентации)